Образец индивидуального задания

ПО КРИВЫМ И ПОВЕРХНОСТЯМ ВТОРОГО ПОРЯДКА

Задача 1

Найти координаты какой-либо точки, принадлежащей данной кривой:

.

Задача 2

Определить тип кривой и построить ее:

.

Задача 3

Найти область, ограниченную линиями:

и .

Задача 4

Найти полярное уравнение и построить кривую

.

Задача 5

Лежит ли точка А(-1,1,2) на поверхности, полученной вращением параболы вокруг оси Ох? Если нет, найдите, по крайней мере одну точку на этой поверхности.

Задача 6

Опишите область, которая получается в сечении фигуры плоскостью хОу.

Задача 7

Найдите точки пересечения прямой с гиперболическим параболоидом .

РЕШЕНИЕ ЗАДАЧ

Решение задачи 1

Пусть, например , тогда . Получили две точки А(3,0) и В(-3,0), принадлежащие данной кривой.

Решение задачи 2

Выделим полные квадраты при х и при у:

.

В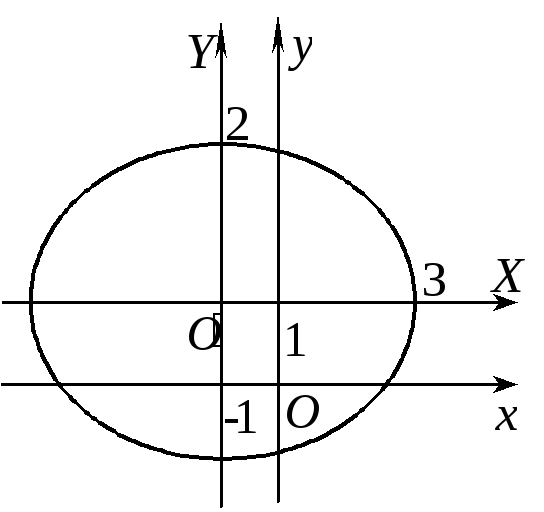ведем новую систему координат, полученную параллельным переносом старой системы на вектор 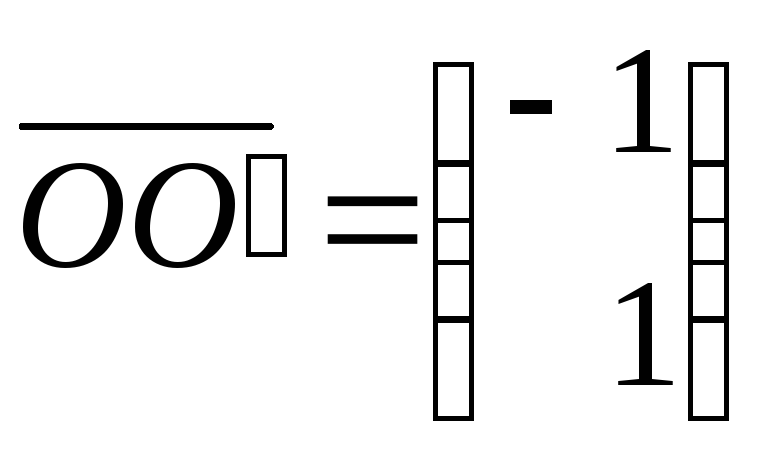. При этом связь между координатами точек плоскости в старой и новой системах выражается формулами: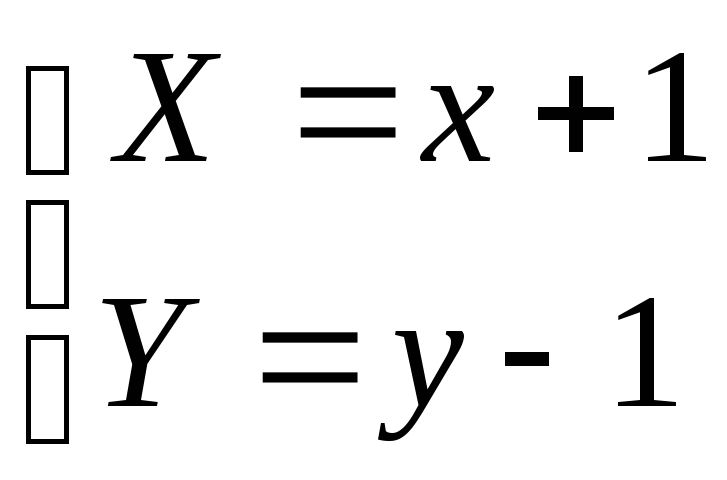. Подставляя это в полученное уравнение, получаем каноническое уравнение .

Решение задачи 3

Найдем точки пересечения этих линий, первая из которых является параболой, а вторая – прямой:

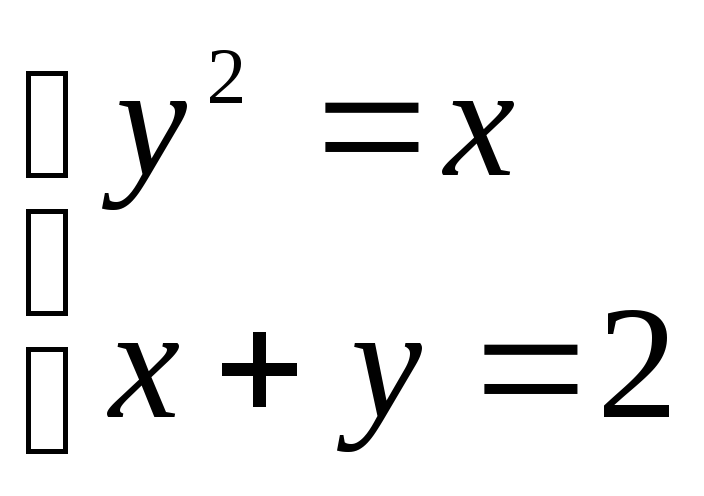
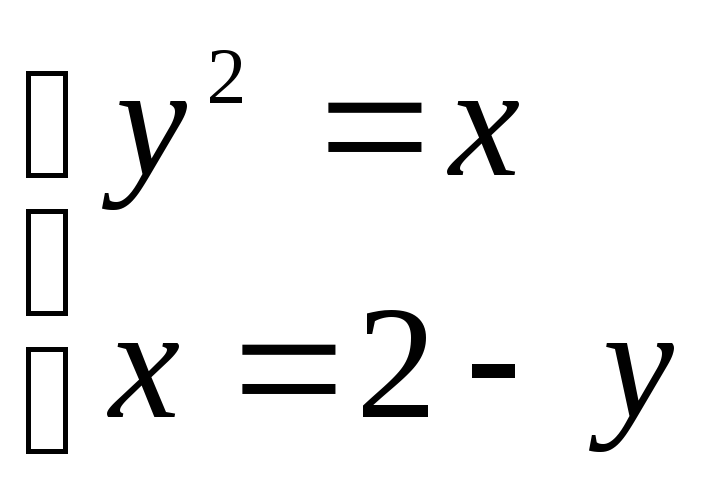
, . Следовательно,,. Получили точки пересеченияи.

П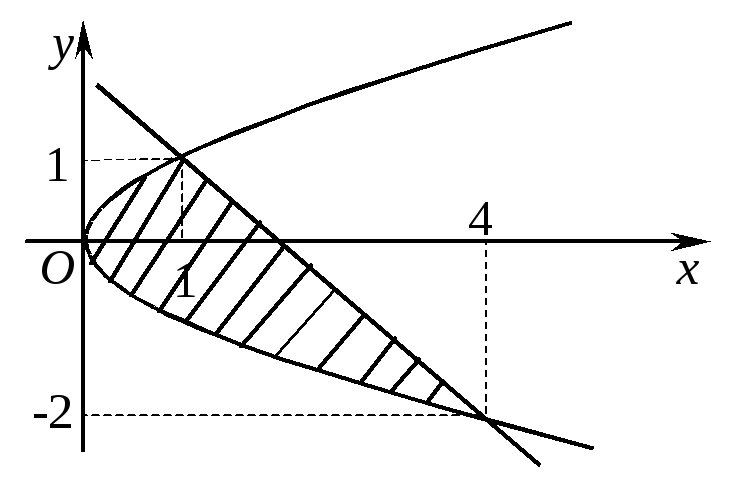ри построении области сначала изображаются точки пересечения, прямая проводится через полученные точки, а для построения параболы нужно найти ещё её вершину, которая в данном случае совпадает с началом координат.

Решение задачи 4

Д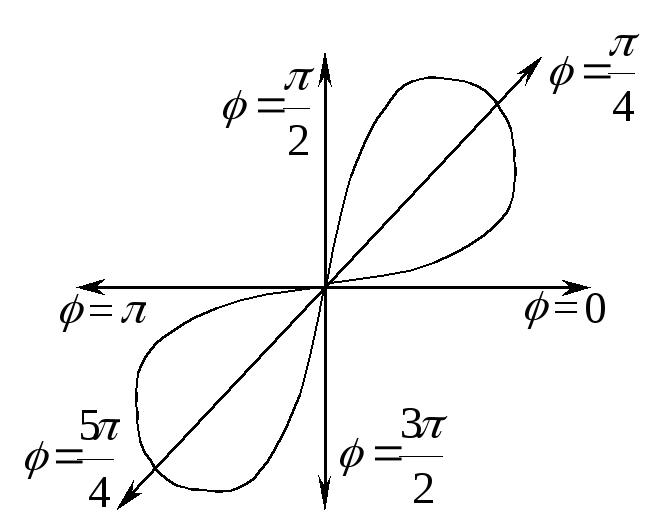ля получения полярного уравнения используем формулы (63):

. Так как синус — периодическая функция, то можно построить таблицу значений на периоде, который для функции составляет интервал от 0 до.

	0
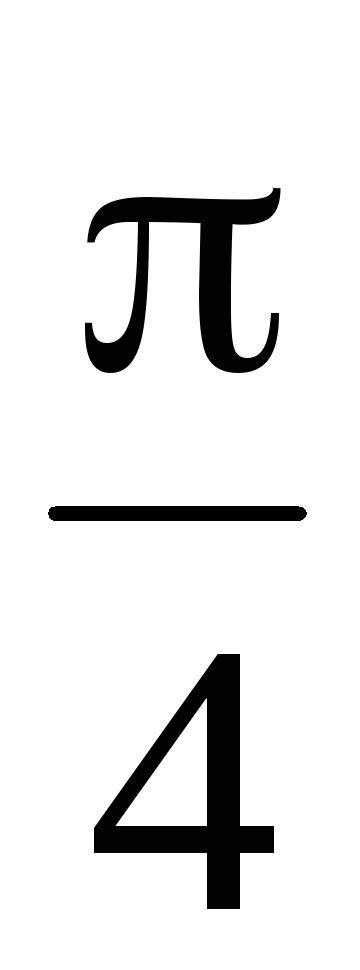
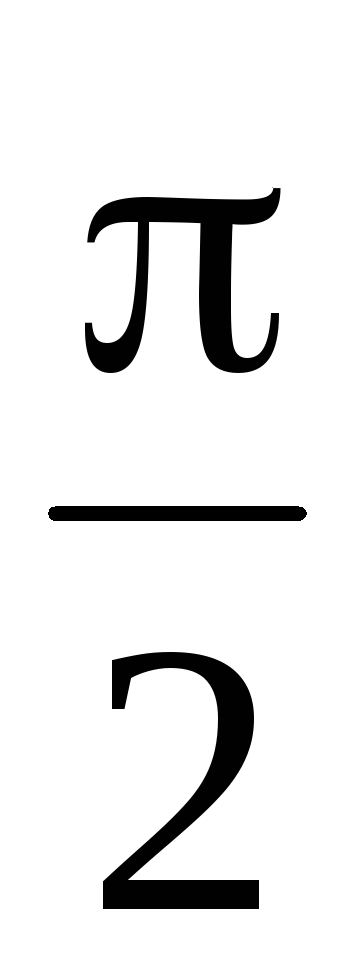
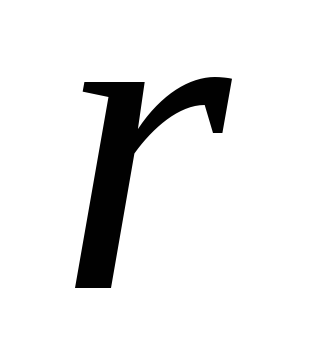
	0	3	0	-	0

На промежутке между и функция, то есть функция не определена на . Аналогичным образом функция ведёт себя на промежуткахи. Полученные точки соединим плавной кривой, которая носит название лемнискаты Бернулли.

Решение задачи 5

С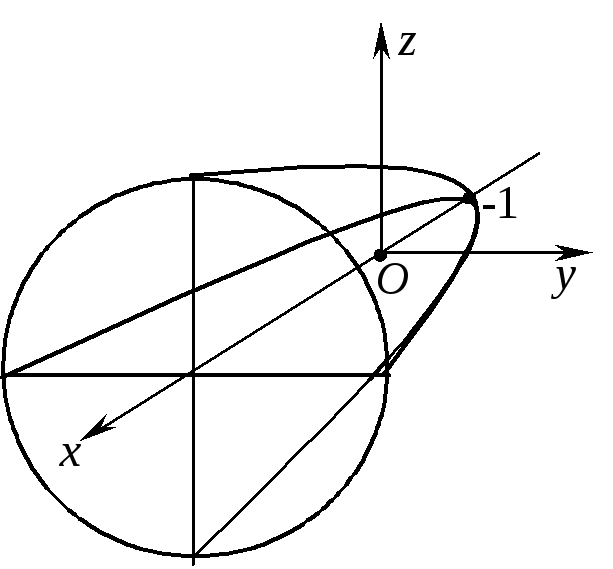начала изобразим получившееся тело. Построим график параболы в плоскостихОу. Затем, вращая параболу вокруг осиОх, получим пространственную фигуру — параболоид вращения (частный случай эллиптического параболоида). Ясно, что сечения этого параболоида плоскостями, перпендикулярными осии проходящими через точкуприбудут окружностями. Это и есть уравнение построенного параболоида вращения.

Точка не удовлетворяет данному уравнению и, таким образом, не принадлежит данной поверхности. Примером точки, лежащей на заданной поверхности, может служить вершина параболлоида с координатами. Другая точка поверхности —.

Решение задачи 6

Заданное уравнение определяет эллипсоид, сечение которого любой плоскостью является эллипсом. Пересекая данный эллипсоид плоскостью хОу, которая имеет уравнение, получаем:

.

Итак, искомое сечение представляет собой эллипс в плоскости хОус центром в точке , с большой полуосью и малой полуосью .