20. В прямую призму, основанием которой является прямоугольный треугольник с углом и гипотенузой с, вписана сфера. Найдите объем призмы.

21. В шар вписана правильная треугольная призма. Радиус шара равен 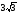см. При какой длине высоты призмы объем ее будет наибольшим?

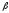22. В основании прямой призмы лежит равнобедренный треугольник с углом при вершине. Диагонали двух равных боковых граней, которые имеют общую вершину, образуют между собой угол. Найдите объем призмы, если радиус цилиндра, описанного около призмы, равен R.

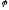23. В основании прямой призмы лежит треугольник с угламии. Диагональ грани, которая содержит прилежащую к данным углам сторону, равнаb и образует с плоскостью основания угол 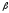. Найдите боковую поверхность цилиндра, вписанного в данную призму.

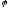24. В основании прямой призмы лежит прямоугольник с углом между диагоналями. Диагональ меньшей боковой грани образует с плоскостью основания угол. Диагональ призмы равнаl. Найдите боковую поверхность цилиндра, описанного около призмы.

25. В правильной четырехугольной пирамиде плоский угол при вершине равен . Найдите объем пирамиды, если радиус шара, описанного около нее, равенR.

26. В шар радиуса R вписана правильная треугольная пирамида с плоским углом при вершине, равным . Найдите объем пирамиды.

Варіант 2

Описати методику розв’язання задачі. Для виділених задач побудувати зображення комбінацій тіл.

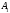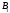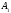
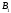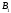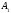1. Прямая а параллельна плоскости . Через точки А и В прямой а проведены параллельныепрямые, пересекающие плоскость в точкахисоответственно. Найдите площадьчетырехугольника АВ, если = 13 см, АА₁ — 14 см, В = 15 см.

2. На плоскости дана трапеция и точка вне ее. Прямые, проходящие через эту точку и вершины трапеции, образуют с ее плоскостью углы равные 45°. Найдите расстояние от этой точки до плоскости трапеции, если один из ее углов равен 60°, а диагональ, выходящая из вершины этого угла равна см.

3. Точка М удалена на расстояние 15 см от каждой стороны параллелограмма и на расстоя­ние 9 см от его плоскости. Найдите площадь этого параллелограмма, если его диагонали относятся как 3 : 4.

4. Внутри трехгранного угла с плоскими углами 90°, 90° и 120° взята точка, удаленная от его граней соответственно на 15 см, 12 см и 12 см. Найдите расстояние от этой точки до вершины угла.

5. Из данной точки проведены к данной плоскости две равные наклонные. Угол между наклонными равен 60° угол между проекциями - прямой. Докажите, что каждая из этих наклонных образует с плоскостью угол 45°

6. Ортогональной проекцией правильного треугольника на плоскость, которая содержит одну из его вершин является равнобедренный треугольник с боковой стороной 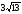см. Сторона правильного треугольника 12 см. Вычислите угол между плоскостями этих треугольников, если одна из сторон треугольника параллельна плоскости проекции.

7. Постройте сечение пятиугольной пирамиды SABCDE плоскостью, проходящей через сторону основания пирамиды АВ и точку N на ребре SD.

8. Концы отрезка А(5; - 2; 1) и В(5; 3; 6). Найдите точку, симметричную середине отрезка относительно плоскости xz.

9. При параллельном переносе точка А (2; 1; - 1) переходит в точку А(1; - 1; 0). В какую точку переходит точка М, симметричная точке А относительно плоскости хОу?

10. Дан прямоугольный параллелепипед 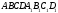. Доказать:

.

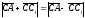11. ) Вычислите длину диагонали АС параллелограмма ABCD, если А (2; - 6; 0),

В(- 4; 8; 2), D (0; - 12; 0).

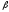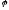12. В основании прямой призмы лежит равнобокая трапеция с боковой стороной d и тупым углом , причем диагонали трапеции взаимно перпендикулярны. Диагональ призмы наклонена к плоскости основания под углом. Найдите объем призмы.

13. Основанием прямой усеченной призмы служит прямоугольный треугольник АВС, в котором катет АС = 15 см и катет ВС = 20 см. Боковые ребра ВВи ССсодержат по 10 см, а АА— 18 см. Определить объем и полную поверхность этой усеченной призмы.

14. В правильной четырехугольной пирамиде боковое ребро равно b, а боковая грань наклонена к плоскости основания под углом . Определить объем пирамиды.

15. В правильной четырехугольной пирамиде SABCD плоскость, проведенная через сторону AD перпендикулярно к грани SBC, делит эту грань на две равновеликие части. Найдите площадь полной поверхности пирамиды, если AD = а.

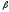16. В основании пирамиды лежит равнобедренный треугольник с углом при вершине. Две равные боковые грани пирамиды перпендикулярны к плоскости основания, а третья грань наклонена к ней под углом. Определите объем пирамиды, если большее ее боковое ребро равноb.

17. Основание пирамиды - параллелограмм с острым углом 30° и сторонами 32 см и 70 см. Боковое ребро длиной 12 см перпендикулярно к плоскости основания. Найдите площадь поверхности пирамиды.

18. В цилиндре параллельно его оси проведена плоскость, которая пересекает нижнее основание по хорде b, которую видно из центра верхнего основания под углом . Диагонали сечения образуютмежду собой угол . Найти объем цилиндра.

19. Зная, что полная поверхность цилиндра равна 105см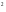,а боковая поверхность составляет 80см². Найти объем цилиндра.

20. В основании прямой призмы лежит равнобедренный треугольник с углом 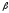при основании. Диагонали двух равных боковых граней, которые имеют общую вершину, образуют между собой угол. Найдите объем призмы, если радиус цилиндра, вписанного в призму равенr.

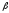21. В основании прямой призмы лежит равнобедренный треугольник с углом при вершине. Диагональ грани, которая содержит сторону основания этого треугольника, наклонена к плоскости основания под углом. Найдите боковую поверхность призмы, если радиус цилиндра, описанного около данной призмы, равен R.

22. Основанием прямой призмы есть ромб с острым углом . Меньшая диагональ призмы наклонена к ее основанию под углом, а большая диагональ равна d. Вычислите боковую поверхность цилиндра, вписанного в данную призму.