Варіант 1

Описати методику розв’язання задачі. Для виділених задач побудувати зображення комбінацій тіл.

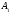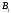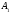
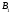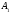
1.Прямая а параллельна плоскости. Через точки А и В прямой а проведены параллельные прямые, пересекающие плоскостьв точкахисоответственно. Найдите площадь четырехугольникаВ, если = 17 см, А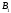= 10 см, В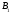= 21 см.

2. Дан треугольник ABC, в котором АB = 9 см, ВС = 12 см, АС = 15 см. На стороне АВ взята точка М так, что AM :MB — 2:1. Через точку М проведена плоскость, параллельная стороне АС и пересекающая сторону ВС в точке К. Найдите площадь треугольника МВК.

3.Отрезок соединяет точки А и В, лежащие на двух взаимно перпендикулярных плоскостях, и образует с одной из них угол 45°. Один из концов отрезка удален от этой плоскости на расстоянии см. Часть линии пересечения плоскостей, заключенная между перпендикулярами, опущенными на нее из концов данного отрезка, равна 2 см. Найдите угол между отрезком и другой плоскостью.

4. Две параллельные прямые АВ и CD лежат в двух пересекающихся плоскостях, которые образуют угол 60°. Точки А и D удалены от линии пересечения плоскостей на расстоянии 8 см и 3 см. Найдите расстояние от плоскости ABD до линии пересечения данных плоскостей.

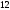
5. Из точки, которая удалена от плоскости на 12 см, проведены две наклонные, длины которых 13 см и 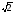см. Угол между проекциями этих наклонных равен 90°. Найдите расстояние от этой точкидо прямой, проходящей через основания наклонных.

6. В равнобедренном треугольнике угол при вершине равен 120°, а боковые стороны по 10 см. Вне треугольника дана точка, удаленная от всех его вершин на 26см. Найдите расстояние от этой точки до плоскости треугольника.

7. Дан куб 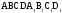. На ребрах АВ и ВС даны точки М и N, которые делят эти ребра пополам. Постройте сечение куба плоскостью, которая проходит через точки М и N параллельно диагонали AD грани куба.

8. Даны точки А (0; 1; - 1), В (1; - 1; 2), С (3; 1; 0), D (2; 1; 1). Найдите угол между векторам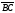и и.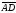

9. На оси аппликат найти точку А, равноудаленную от точек М(- 2; 3; 5) и

N (3; -5; 1).

10. Даны три точки А (0; 1; - 1), В (1; - 1; 2), С (3; 1; 0). Вычислите косинус угла С треугольника АВС.

11. При каких значениях m и n векторы 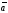(- 1; 4; - 2) и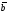(- 3;m; n) коллинеарны?

12. В основании прямой призмы лежит ромб, меньшая диагональ которого равна d. Большая диагональ призмы, образует с плоскостью основания 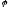угол , а диагональ боковой грани - угол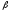. Найдите объем призмы.

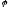13. В основании прямой призмы лежит прямоугольник. Диагональ призмы образует с плоскостью основания угол , а диагональ одной из боковых граней равнаl и образует с плоскостью основания угол . Найдите объем призмы.

14. В правильной четырехугольной пирамиде апофема равна l, а боковое ребро образует с плоскостью основания угол 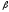. Найти объем пирамиды.

15. В правильной четырехугольной пирамиде SABCD сторона основания равна 4 см. Через сторону CD основания проведено сечение, которое пересекает грань SAB по средней линии треугольника SABSAB. Площадь сечения равна 18 см. Найдите объем пирамиды SABCD.

16. В основании пирамиды лежит прямоугольная трапеция с большей боковой стороною d и острым углом . Все боковые грани пирамиды наклонены к плоскости основания под углом. Найти объем пирамиды.

17. Найдите объем правильной усеченной четырехугольной пирамиды, если стороны оснований равны а и b (а >b), а острый угол боковой грани равен .

18. В усеченном конусе, отношение площадей оснований которого равно 4, образующая длиной 4 см наклонена к плоскости основания под углом в 30°. Определить объем этого конуса.

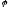19. Через две образующие конуса проведена плоскость, которая наклонена к плоскости основания под углом . Эта плоскость пересекает основание конуса по хорде, которую видно из центра его основания под углом. Найдите объем конуса, если его образующая равнаl.