20. В правильной треугольной пирамиде боковая грань наклонена к плоскости основания под углом . Найдите полную поверхность пирамиды, если радиус шара, вписанного в нее, равенr.

21. Апофема правильной треугольной пирамиды равна h. Боковое ребро образует с высотой угол . Найдите объем описанного шара.

22. В равнобедренной трапеции диагональ перпендикулярна к боковой стороне. Боковая сторона равна а и образует с большим основанием угол . Определите объем тела, полученного при вращении трапеции вокруг большего основания.

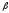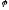23. В основании пирамиды лежит равнобедренный треугольник, сторона основания которого равна а и углом при основании . Все боковые грани наклонены под угломк основанию. Найдите площадь поверхности вписанного шара.

24. В конус вписан шар радиуса r. Образующая конуса наклонена к плоскости основания под утлом. Найдите объем конуса.

25. Прямоугольный треугольник с катетом а и прилежащим к нему углом 60° вращается вокруг оси, проходящей через вершину данного острого угла перпендикулярно катету. Найдите площадь поверхности тела вращения.

26. Ромб со стороной а и острым углом вращается вокруг оси, которая проходит через вершину острого угла перпендикулярно к его стороне. Найдите поверхность тела вращения

Варіант 13

Описати методику розв’язання задачі. Для виділених задач побудувати зображення комбінацій тіл.

1. Равные равнобедренные треугольники MNK и MKL имеют общее основание МК, а их плоскости образуют угол 60°. Найдите боковые стороны треугольников MNK иМКL, если их основания равны по 3 см, а расстояние между точками N и L равно 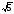см.

2. Если точка равноудалена от двух сторон треугольника и перпендикуляр, проведенный через эту точку к плоскости треугольника, пересекает третью сторону, то основание этого перпендикуляра принадлежит биссектрисе угла, противолежащего третьей стороне. Докажите это.

3. Из точки пространства к плоскости прямоугольной трапеции, большее основание которой равно 24 см, а большая боковая сторона - 25 см, проведен перпендикуляр, длина которого 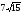см. Основание перпендикуляра - вершина тупого угла трапеции, большая диагональ которой является биссектрисой прямого угла. Вычислите расстояние от данной точки до вершины другого прямого угла.

4. В прямоугольной трапеции основания равны 10 см и 15 см. Расстояние от некоторой точки до плоскости трапеции равно 8 см. Расстояния от этой точки до каждой стороны трапеции равны. Вычислите это расстояние.

5. Внутри трехгранного угла С прямыми плоскими углами взята точка. Найдите расстояние от этой точки до вершины трехгранного угла, если она удалена от ребер соответственно на 20 см, 31 см, 33 см.

6.Расстояние между параллельными прямыми, которые лежат в гранях двугранного угла, 7 см. Они удалены от его ребра на расстояние 3 см и 5 см. Найдите величину этого двугранного угла.

7. Постройте общий перпендикуляр диагонали BD куба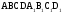и ребра АА, не пересекающего эту диагональ.

8. Даны вершины треугольника ABC: А (- 2; 0; 1), В (8; - 4; 9), С (- 1; 2; 3). Вычислите длину медианы, проведенной из вершины С.

9. Вычислите длину медианы ВВтреугольника с вершинами А(4; 0; -8), В(2; 0; 3), С(16; 2; 0).

10. Докажите, что треугольник с вершинами А(1; 0; 1), В (1; 1; 0) и С (1; 1; 1) прямоугольный. Найдите расстояние от начала координат до центра окружности, описанной около этого треугольника.

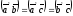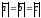11. Дано: =60°. Вычислите скалярное произведение, если=1.

12. Все ребра прямой треугольной призмы имеют одинаковую длину. Площадь полной поверхности призмы равна (4 + 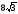) см. Найти площадь ее основания.

13. В основании прямой призмы лежит равнобедренный треугольник с основанием а и углом при вершине. Плоскость сечения, проходящая через боковую сторону нижнего основания и противолежащую вершину верхнего основания, образует с основанием угол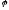. Найти объем призмы.

14. Площади оснований усеченной пирамиды равны 18 м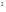и 128 м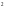. Определить площадь параллельного сечения, делящего высоту в отношении 2:3, начиная от меньшего основания.

15. Боковая поверхность правильной треугольной пирамиды равна 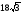см, а полная поверхность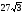см. Высота пирамиды разделена на три равные части и через точки деления проведены сечения параллельно основанию. Определите объем усеченной пирамиды, ограни­ченной этими параллельными сечениями.

16. В основании пирамиды лежит прямоугольный треугольник с углом . Две боковые грани, содержащие стороны этого угла, перпендикулярны к плоскости основания, а третья грань наклонена к ней под углом. Найдите объем пирамиды, если большее боковое ребро равноl.

17. Основание пирамиды - ромб с диагоналями 30 см и 40 см. Боковое ребро длиной 18 см перпендикулярно плоскости основания. Найдите площадь поверхности пирамиды.

18. В усеченном конусе образующая равна 5 см, а радиусы оснований 6 см и 10 см. Найдите радиус цилиндра такой же высоты, полная поверхность которого равновелика боковой поверхности данного усеченного конуса.

19. В усеченном конусе высота, образующая и боковая поверхность равны соответственно Н, L и S. Определите площадь осевого сечения.

20. В правильной четырехугольной пирамиде расстояние от середины высоты пирамиды к боковой грани равняется d. Найдите полную поверхность вписанного в пирамиду конуса, образующая которого наклонена к плоскости основания под углом .