24. Угол между образующей конуса и его высотой равен . Расстояние от центра описанного около конуса шара до основания высоты равноl. Вычислите полную поверхность конуса.

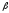25. В нижнем основании цилиндра проведена хорда длиной а, которую видно из центра этого основания под углом . Отрезок, соединяющий центр верхнего основания с точкой окружности нижнего основания, образует с плоскостью основания угол. Найдите объем описанного около цилиндра шара.

26. Треугольник со сторонами 12 см, 17 см и 15 см вращается вокруг меньшей стороны. Найдите площадь поверхности тела вращения. Варіант 10

Описати методику розв’язання задачі. Для виділених задач побудувати зображення комбінацій тіл.

1. Дан параллелограмм ABCD и точка S вне плоскости параллелограмма.

АВ=15 см, AD=20 см, SB — 9 см, причем плоскости SAB и SBC перпендикулярны плоскости параллелограмма. Найдите расстояние от точки Sдо АС, если известно, что АС = BD.

2. Расстояние от точки до плоскости равно 4 см. Из этой точки проведены две наклонные, длина которых 5 см и см. Угол между проекциями этих наклонных равен 60°. Вычислите расстояние между основаниями этих наклонных.

3. Ортогональной проекцией четырехугольника с площадью 144 см² является прямоугольник, диагональ которого равна 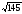см, а одна из сторон 8 см. Вычислите угол между плоскостями пря­моугольника и данного четырехугольника. Может ли данный четырехугольник быть квадратом?

4. Из некоторой точки пространства к плоскости треугольника, стороны которого равны 32 см, 40 см, 48 см, проведен перпендикуляр, длина которого 18 см. Основание перпендикуляра принадлежит стороне треугольника, равной 40 см, а две другие стороны равноудалены от данной точки. Вычислите расстояние от данной точки до других сторон.

5. Два равнобедренных треугольника имеют общее основание, а их плоскости образуют между собой угол в 60°. Общее основание равно 16 см. Боковая сторона одного треугольника равна 17 см, а боковые стороны другого - взаимно перпендикулярны. Вычислите расстояние между вершинами треугольников

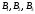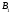6. Три плоскости параллельны. Одна прямая пересекает их: в точках ; другая - в точках.Известно, что АА₂=4 см, В₂В₃=9 см, А₂А₃=BB₂. Найдите длины отрезков АА₃ и В₃.

7. Постройте сечение пирамиды SABCDE плоскостью, проходящей через диагональ основа­ния AD, и параллельной боковому ребру SE.

8. Даны точки А(5; - 4; 2), В(5; - 7; 8), С(2; 2; - 7), D(- 1; 5; -10). Покажите, что векторы 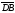и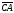коллинеарны; установите, как они направлены - одинаково или противоположно.

9. Докажите, что точки A(- 4; - 8; 8) , В (- 2; - 2; 6), С (4; 0; - 10), D(2; - 6; - 8) являются вершинами параллелограмма ABCD.

10. Даны три точки А (0; 1; - 1), В (1; - 1; 2), С (3; 1; 0). Вычислите косинус угла А треугольника АВС.

11. В тетраэдре ABCD точка К - середина ребра DC. Выразить через векторы =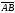,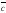=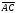,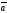=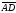вектор.

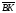12. В основании прямой призмы лежит равнобедренный треугольник с уг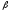лом при вершине. Диагонали двух боковых граней, которые содержат стороны этого угла, наклонены к плоскости основания под утлом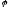. Диагональ третьей боковой грани равнаl. Определите объем призмы.

13. В основании прямой призмы лежит равнобокая трапеция с острым углом и меньшим основанием а. Диагонали трапеции являются биссектрисами острых углов. Диагональ призмы наклонена к плоскости основания под углом. Найдите объем призмы.

14. В основании пирамиды лежит ромб. Две смежные боковые грани ее перпендикулярны к плоскости основания и образуют между собой тупой угол , а две другие боковые грани наклонены к плоскости основания под углом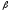. Определите боковую поверхность пирамиды, если высота пирамиды равна h.

15. Боковая грань правильной усеченной четырехугольной пирамиды наклонена к плоскости большего основания под углом . Площадь нижнего основания пирамиды в девять раз больше площади верхнего основания, а ее объем равен V. Найдите боковую поверхность пирамиды.

16. В основании пирамиды лежит ромб с углом 30°. Две боковые грани, образующие тупой двугранный угол, перпендикулярны к основанию. Какова должна быть длина стороны ромба, чтобы площадь каждой из двух других боковых граней была наибольшей, если большее боковое ребро равно 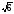дм?

17. Площади оснований и диагонального сечения правильной четырехугольной усеченной пирамиды соответственно равны 16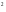 дм, 324 дм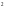и 88 дм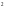, Найдите площадь боковой поверхности усеченной пирамиды.

18. В цилиндре параллельно его оси проведена плоскость, которая пересекает нижнее основание по хорде а. Диагональ сечения наклонена к плоскости основания под углом . Отрезок, который соединяет центр верхнего основания с серединой хорды нижнего основания, образует с плоскостьюнижнего основания угол 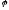. Найти объем цилиндра.

19. Образующая конуса равна см. Найти площадь полной поверхности конуса, если угол при вершине осевого сечения конуса прямой.

20. В основании прямой призмы лежит прямоугольный треугольник с углом . Через противолежащий катет нижнего основания и вершину углаверхнего основания проведено сечение, которое образует с плоскостью основания угол. Перпендикуляр, проведенный из вершины угланижнего основания до сечения, равен а. Найдите объем цилиндра, описанного около этой призмы.

21. В цилиндр вписан прямоугольный параллелепипед, большая сторона основания которого равна а. Диагональ параллелепипеда составляет с его большей боковой гранью угол 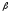, а с плоскостью основания угол. Найдите площадь боковой поверхности цилиндра.

22. В правильной треугольной пирамиде расстояние от центра вписанного в нее шара до стороны основания равно d. Определите полную поверхность пирамиды, если боковая грань ее наклонена к плоскости основания под углом .

23. В основании пирамиды лежит равнобедренный треугольник с углом при вершине. Все боковые грани пирамиды наклонены к плоскости основания под углом. Вычислите объем пирамиды, если радиус шара, вписанного в нее, равенr.

24. В основании пирамиды лежит прямоугольный треугольник с углом 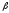. Все боковые грани пирамиды наклонены к плоскости основания под углом. Найдите объем пирамиды, если радиус шара, вписанного в нее, равенr.