Дипольный момент

Электрическим моментом диполя или дипольным моментом называется вектор 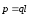, совпадающий по направлению с плечом диполя и равный произведению заряда 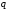на плечо.

Применение принципа суперпозиции для расчета поля диполя

В соответствии с принципом суперпозиции полей, напряженность в произвольной точке поля диполя равна:

,

_где 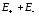- напряженности полей зарядов и

Поведение диполя во внешнем электрическом поле.

Поведение диполя во внешнем однородном электрическом поле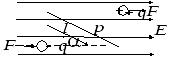

Поле действует на заряды с силой, определяемой формулой

,

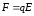поэтому действующая на положительный заряд сила направлена в ту же сторону, что и вектор , а сила, действующая на отрицательный заряд, направлена в противоположную сторону. Эти силы образуют пару, плечо которой равно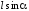, т.е. зависит от ориентации диполя относительно поля.

Момент пары сил

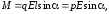
стремится повернуть диполь так, чтобы его дипольный электрический момент установился по направлению поля. Кроме того, эта пара сил приводит к растяжению диполя, если диполь не является жестким, и расстояниеl может меняться.

5. Поток вектора напряженности. Теорема Остроградского-Гаусса для электростатического поля в вакууме. Поток вектора напряженности.

Величина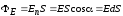(5)

называется потоком вектора напряженности через площадку S. Здесь 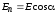– проекция векторана нормаль к поверхности.- вектор, модуль которого равенS, а направление совпадает с направлением нормали к площадке.

элементарный поток сквозь участок поверхности площадью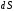равен:.

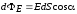Полный поток 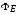сквозь произвольную поверхность S найдем в результате суммирования (интегрирования) всех элементарных потоков.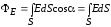

Поток вектора напряженности сквозь замкнутую поверхность S. Для произвольной замкнутой поверхности S поток вектора сквозь эту поверхность равен.

Теорема Остроградского-Гаусса для электростатического поля в вакууме

Теорема Гаусса (в случае дискретного распределения зарядов). Поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на электрическую постоянную .

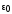Рассмотрим поток вектора сквозь сферическую поверхность радиусаr, охватывающую точечный заряд Q (рис. 2.6).

В соответствии с формулой (6) поток вектора напряженности сквозь сферическую поверхность радиуса r, охватывающую точечный заряд Q, находящийся в ее центре, равен:

(7)

Этот результат справедлив для замкнутой поверхности любой формы. Так, если окружить сферу произвольной замкнутой поверхностью, то каждая линия напряженности, пронизывающая сферу пройдет и через поверхность.

Поток вектора сквозь произвольную замкнутую поверхность, окружающуюn зарядов (поле, создаваемое системой точечных зарядов)

Согласно принципу суперпозиции , поэтому

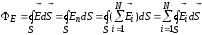. (8)

Интеграл суммы равен сумме интегралов, и каждый из интегралов, стоящий под знаком  равен 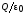_, поэтому,

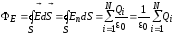Теорема Гаусса (в случае непрерывного распределения зарядов). Поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен заряду, заключенному в объеме, ограниченном этой поверхностью, и деленному на .

объемную плотность заряда - физическую величину, определяемую зарядом, приходящимся на единицу объема. Суммарный заряд, заключенный внутри замкнутой поверхностиS, охватывающей некоторый объем V:

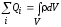. (10)

С учетом этого теорему Гаусса можно записать:

.

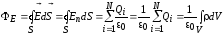6. Работа перемещения заряда в электростатическом поле. Теорема о циркуляции вектора напряженности электростатического поля. Потенциал электростатического поля. Разность потенциалов. Связь напряженности и потенциала. Эквипотенциальные поверхности.

Работа перемещения заряда в электростатическом поле

Перемещение пробного заряда в поле точечного зарядаQ происходит под действием сил электростатического поля. Работа силы 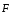на элементарном перемещенииравна (рис. 3.1):,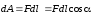

где 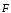– кулоновская сила. Так как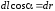, то

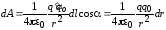. (1)

Работа при перемещении заряда 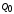на конечном пути в поле зарядаQ из точки 1 в точку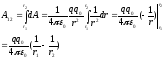 2:. (2)

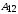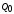Работа не зависит от формы траектории, а определяется начальным и конечным положением заряда. Следовательно, электростатическое поле точечного заряда – потенциально, а сила Кулона – консервативная сила.