42. Затухающие колебания

Гармонические колебания относятся к свободным колебаниям без трения, которые происходят в системе, предоставленной самой себе после того, как она была тем или иным способом выведена из состояния равновесия. Свободные колебания любого осциллятора в отсутствии трения будут гармоническими, если действующая сила (или момент силы) является квазиупругой, т.е. силой, направленной к положению равновесия и зависящей от смещения из этого положения линейно. Частота и период свободных колебаний без трения зависят только от свойств самого осциллятора, в отличие от амплитуды колебаний и начальной фазы, которые определяются начальными условиями.

В любой реальной колебательной системе есть силы сопротивления (трения), действия которых приводит к уменьшению амплитуды и энергии колебаний. Такие свободные колебания называются затухающими. Дифференциальное уравнение свободных затухающих колебаний линейной системы, у которой параметры, определяющие физические свойства системы в ходе процесса не изменяются, задается в виде

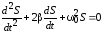, (1)

где 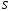- колеблющаяся величина, описывающая физический процесс;- коэффициент затухания;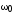- циклическая частота свободных незатухающих колебаний при(при отсутствии потерь энергии) илисобственная частота колебательной системы.

Уравнение (1) при условии описывает затухающие колебания и его решение имеет вид

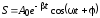, (2)

где - амплитуда затухающих колебаний;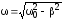- частота затухающих колебаний.

Зависим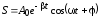ость показана на рис. 15.1 сплошной линией, а зависимость- штриховыми линиями.

Рис. 15.1

Видно, что эта функция (2) не периодическая. Тем не менее, величину принято называть периодом затухающих колебаний, если затухание мало. Таким образом, промежуток времени между двумя последующими максимумами или минимумами колеблющейся физической величины условно называется периодом затухающих колебаний

.

Характеристики затухающих колебаний. Кроме коэффициента  затухание характеризуют и другими величинами:

1. Время релаксации  - это промежуток времени , в течении которого амплитуда затухающего колебания уменьшается ве раз.

2. Логарифмический декремент затухания. Его определяют как

, (3)

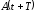где и- амплитуды двух последовательных колебаний, соответствующих моментам времени, отличающимся на период;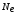- число колебаний, совершаемых за время уменьшения амплитуды в е раз. При малом затухании () характеризует относительное уменьшение амплитуды колебаний за период. Для данной колебательной системы логарифмический декремент затухания – постоянная величина.

3. Добротность осциллятора. По определению (при малом затухании ())

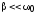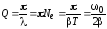. (4)

Из формулы (4) следует, что добротность пропорциональна числу колебаний , совершаемых системой за время релаксации.

При достаточно большом затухании () система совершаетапериодическое движение: выведенная из равновесия, она возвращается в это положение, не совершая колебаний.

Выводы, полученные для свободных затухающих колебаний линейных систем, применимы для колебаний различной физической природы – механических (пружинный маятник) и электромагнитных (электрический колебательный контур).

В качестве примера рассмотрим свободные затухающие колебания пружинного маятника. Пусть пружинный маятник массы т совершает малые колебания под действием упругой силы . Если на маятник, кроме квазиупругой силыдействует сила сопротивления (трения), пропорциональная скорости

,

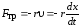где - коэффициент сопротивления, то маятник будет совершать затухающие колебания.

При этих условиях уравнение движения маятника будет иметь вид

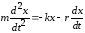. (5)

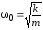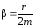Разделим уравнение на величину т и введем и- собственную частотумаятника и коэффициент затухания, соответственно. Тогда дифференциальное уравнение затухающих колебаний маятника:

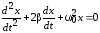. (6)

Решение этого уравнения имеет вид

,

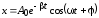где частота

.

Добротность пружинного маятника, согласно определению (4)

равна

. (7)