33 Намагниченность. Магнитное поле в веществе Связь между намагниченностью и напряженностью магнитного поля. Магнитная восприимчивость. Магнитная проницаемость вещества.
Для количественного описания намагниченности магнетиков вводят векторную величину – намагниченность – магнитный момент единицы объема магнетика:
. (8)
Магнитный момент магнетика – сумма магнитных моментов отдельных молекул:
.
Связь
между векторами
и
.
Существует линейная зависимость между
намагниченностью и напряженностью
поля, вызывающего намагничевание
(соблюдается в случае несильных полей)
, (9)
где
- магнитная
восприимчивость вещества.
- безразмерная величина. Для диамагнетиков
(поле молекулярных токов противоположно
внешнему), для пармагнетиков
(поле молекулярных токов совпадает с
внешним).
Для
парамагнетиков:
(O2
(жидкий)
)
Для
диамагнетиков:
(N2
(газ)
)
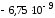Магнитное
поле в веществе
складывается из двух полей: внешнего
поля, создаваемого током и поля,
создаваемого намагниченным веществом.
Вектор
магнитной индукции результирующего
поля в
магнетике равен векторной сумме магнитных
индукций внешнего поля
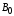и поля
микротоков
:
, (10)
где
- вектор магнитной индукции, характеризующий
магнитное поле макротоков;
- вектор магнитной индукции, характеризующий
магнитное поле микротоков.
Для
описания поля микротоков рассмотрим
магнетик в виде кругового цилиндра
сечения S
и длины l,
внесенного в однородное внешнее магнитное
поле с индукцией
.
Возникающее
в магнетике магнитное поле микротоков
будет направлено противоположно внешнему
полю для диамагнетиков и совпадать с
ним для парамагнетиков. Плоскости всех
микротоков расположатся перпендикулярно
вектору
,
т.к. векторы
их магнитных моментов
параллельны
(для
парамагнетиков) и антипараллельны
(для
диамагнетиков).
Если рассмотреть любое сечение цилиндра, перпендикулярное его оси, то во внутренних участках сечения магнетика молекулярные токи соседних атомов направлены навстречу друг другу и взаимно компенсируются (рис. 11.2). Нескомпенсированными будут молекулярные токи, выходящие на боковую поверхность цилиндра.
Рис. 11.2
Ток,
текущий по боковой поверхности цилиндра,
подобен току соленоида и создает внутри
него магнитное поле, магнитную индукцию
которого можно вычислить по формуле
для магнитной индукции поля внутри
соленоида (в вакууме)
.
Для N = 1 (соленоид из одного витка):
, (11)
-
сила
молекулярного тока, l
– длина рассматриваемого цилиндра,
μ0
= 1 – магнитная постоянная.
С
другой стороны,
это линейная плотность тока (ток,
приходящийся на единицу длины цилиндра).
Магнитный момент такого тока
, (12)
где V – объем магнетика.
Тогда,
согласно формуле (8) намагниченность
равна:
. (13)
Сопоставляя формулы (11) и (13), получим выражение для магнитного поля микротоков:
. (14)
Таким образом, магнитное поле в веществе:
(15)
откуда видно, что
. (16)
Безразмерная
величина
называется
магнитной
проницаемостью вещества.
Для парамагнетиков μ > 1, для диамагнетиков μ < 1.
С учетом этого, магнитное поле макро- и микротоков:
(17)