Лекция 4 теорема об эквивалентности

Для эквивалентности двух систем сил необходимо и достаточно, чтобы были равны их главные векторы и главные моменты относительно любого произвольного центра.

Пусть имеем две системы сил

.

Запишем теорему схематически.

Достаточность Необходимость т.О  произвольная Условие теоремы Утверждение теоремы

Докажем сначала необходимость .

Дано: .

Доказать: , точкаО  произвольная точка пространства.

Доказательство:

Из условия по определению эквивалентности системы сил следует существование такой системы силчто

По основной теореме статики из первого условия следует

. (4.1)

Из второго условия следует

. (4.2)

По определению

(4.3)

(4.4)

Из формулы (4.3) и (4.4) следует

(4.5.)

Сравнивая формулы (4.5), получим

.

Далее аналогично

(4.6)

Из формулы (4.6) следует

(4.7)

Откуда

.

Докажем достаточность.

Дано: , точкаО  произвольная точка пространства.

Доказать: .

Доказательство:

Добавим к обеим системам систему сил с противоравными системесилами:

Найдем главный вектор и главный момент системы сил :

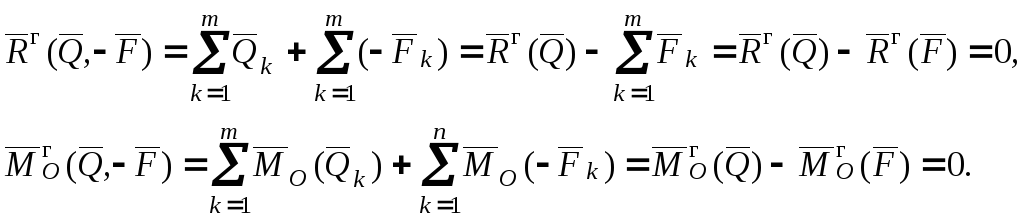
На основании основной теоремы статики

Но и .

Следовательно, по определению эквивалентности систем сил

.

Теорема доказана.

На практике при вычислениях моментов сил часто используется теорема Вариньона, которая непосредственно следует из теоремы эквивалентности.

Теорема Вариньона

Если система сил имеет равнодействующую, то момент равнодействующей относительно произвольной точки (либо оси) равен соответственно геометрической (или алгебраической) сумме моментов сил системы относительно той же точки (либо оси).

Дано: ,

где  равнодействующая.

Доказать: , точкаО  произвольная точка пространства

,

где z - неподвижная ось.

Доказательство:

Воспользуемся вторым условием эквивалентности систем сил:

.

По определению главного момента системы сил

.

Следовательно

. (4.8)

Проектируя (4.8) на ось z получим

. (4.9)

Теорема доказана.

На основании основной теоремы статики доказывается теорема о трех непараллельных силах также используемая при решении практических задач.

Теорема о трех непараллельных силах

Если под действием трех непараллельных сил твердое тело находится в равновесии, то все силы необходимо пересекаются в одной точке.

Доказательство:

Пусть даны три непараллельные силы . Возьмем точкуО, например, на линии действия силы (рис.4.1)

Рис.4.1

Тогда на основании основной теоремы статики

.

Так как , то.

Следовательно силы илежат в одной плоскости, проходящей через точкуО и так как они не параллельны, то линии их действия пересекаются, пусть в точке А.

Заменив их на равнодействующую по аксиоме А1, получим, что линия действия силыдолжна проходить через точкуА.

Теорема доказана.

Рис.4.2

Пример. Рама АВСD, изображенная на рис.4.2, концом А закреплена на неподвижной опоре цилиндрическим шарниром, а концом D положена на подвижный каток. Определить опорные реакции и, возникающие при действии горизонтальной силыприложенной в точкеВ. Весом рамы пренебречь.

Решение. Рама находится в равновесии под действием трех непараллельных сил ,,. Реакция подвижной опорынаправлена по нормали к опорной поверхности. Линию действия реакцииопределим из теоремы о трех непараллельных силах, соединив точкуА с точкой пересечения С силы и реакции.

Определим угол  из прямоугольного треугольника АВС.

.

Зная угол , реакции опор можно определить геометрически из силового треугольника (рис.4.3), либо аналитически, составив уравнения равновесия.

Рис.4.3

Из прямоугольного силового треугольника .

Решим задачу, составив уравнения равновесия для плоской сходящейся системы сил, направив координатные оси согласно рис.4.2:

(4.10)

Из уравнений (4.10) .