FTF 1 semestr.MAVRODI / 63
.pdf
Задачи, приводящие к понятию определенного интеграла
17.1.1. Задача о площади криволинейной трапеции
О: Под криволинейной трапецией пониматся фигура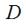
, которая имеет границу
в данном случае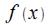
является непрерывной (рис. 17.1).
Вычислим площадь криволинейной трапеции. Для этого следует разделить отрезок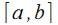
с помощью точек
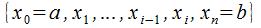на
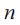элементарных отрезков
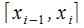. Отметим
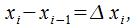определим случайные точки
и отобразим ступенчатую фигуру,
состоящую из прямоугольников с высотами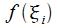
и основаниями
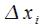. Площадь ступенчатой фигуры
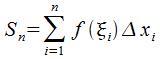и определяет приблизительное значение площади криволинейной трапеции. В
качестве точного значения площади запишем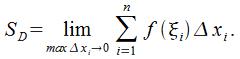
Рис. 17.1
17.1.2. Задача о работе переменной силы
Определим работу переменной силы
, для которой характерно постоянное направление. Под
дествием этой силы материальная точка меняет свое расположение и перемещается из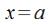
в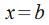
по прямой, имеющей направление вдоль линии действия силы (рис. 17.2).
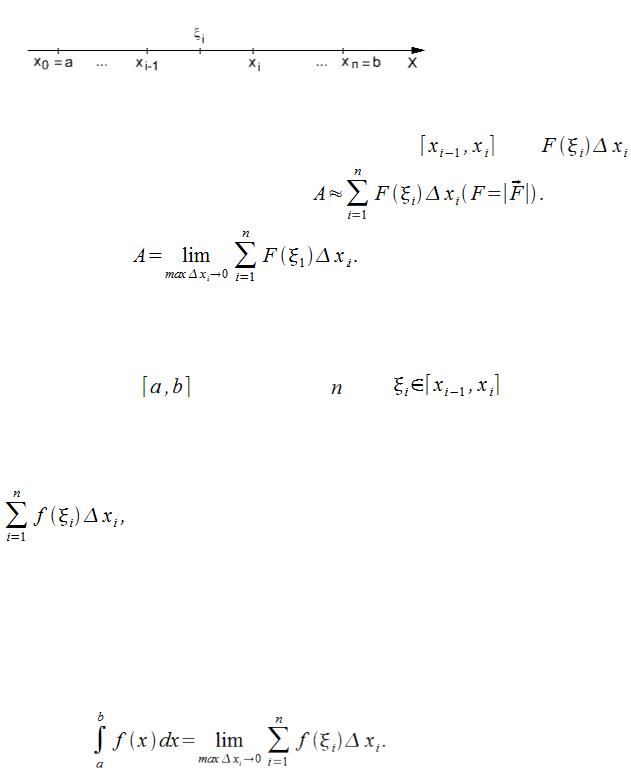
Рис. 17.2 |
|
|
|
Осуществим деление, подобно тому, как было сделано в п.17.1.1: |
равна |
. |
|
Приближенное значение работы на всем пути — |
|
В качестве точного |
|
значения обозначим |
|
|
|
17.1.3. Понятие определенного интеграла |
|
|
|
Предположим, что на |
определена функция частей |
и запишем сумму |
|
(17.1) |
|
|
|
которая именуется интегральной.
О: Под определенным интегралом (о.и.) от функции
и от выбора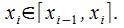
Обозначение:
Числа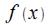
именуют интегрируемой (по Риману) на
.
Т. существования: При условии, что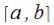
.
В соответствии с определением о.и. отметим, что интеграл имеет зависимость от вида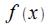
, пределов
и
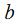, однако не зависит от символа обозначения переменной
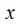, иначе выражаясь
(17.2)
Всоответствии с п.17.1.1 и 17.1.2 и определением о.и. запишем формулы площади криволинейной трапеции:
,работы силы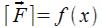
на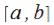
: