52
Саратовский
государственный университет им. Н.Г.
Чернышевского
В.Л. Израйлевич,
И.А. Кузнецова, О.А. Мыльцина, И.Я. Чернявский
Сборник задач по
теории вероятностей и математической
статистике
Часть 2
Случайные процессы
2009 Оглавление
Предисловие 3
1.Введение в теорию
случайных процессов 4
2. Дискретные
марковские цепи. 6
3. Корреляционная
теория случайных процессов 19
4. Условные
математические ожидания 23
5. Винеровский
процесс и интегралы Ито 24
Решения. 26
2. Дискретные
марковские цепи. 26
4. Условные
математические ожидания 45
5. Винеровский
процесс и интеграл Ито 48
Ответы (Дискретные
марковские цепи) 50
Предисловие
Предлагаемый
сборник задач предназначен для
использования на семинарских занятиях
по курсу «Теория случайных процессов»
для студентов механико-математического
факультета. Его цель – помочь студентам,
овладевшим основами теории вероятностей,
познакомиться с основными понятиями
теории случайных процессов и овладеть
методами решения задач, связанных с
дискретными цепями Маркова, корреляционной
теорией случайных процессов, винеровским
процессом, интегралом Ито и стохастическими
дифференциальными уравнениями. Отдельный
раздел посвящен очень интересной теме
– условные математические ожидания
относительно σ – алгебры. Для части
задач приведены решения. При составлении
сборника использовались и известные
задачи, возникшие в результате
педагогической деятельности авторов.
Авторы будут
благодарны за любые замечания,
способствующие улучшению данного
пособия.
Введение в теорию случайных процессов
Задачи
Является
ли событием множество
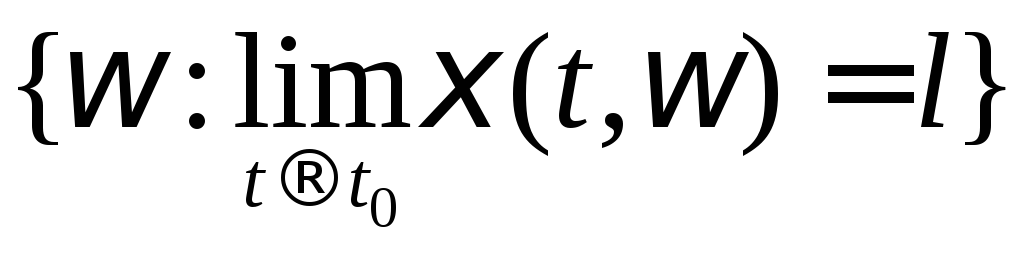 ? ? |
Является
ли событием множество
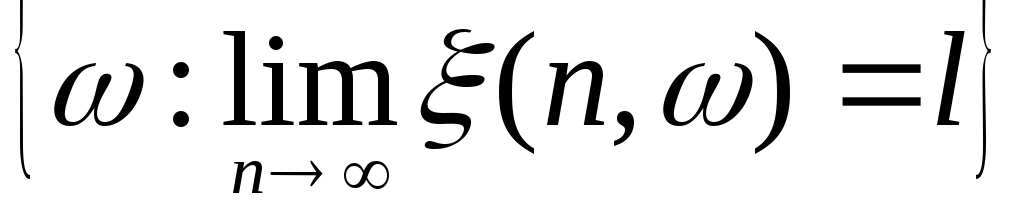 ? ? |
Является
ли событием множество
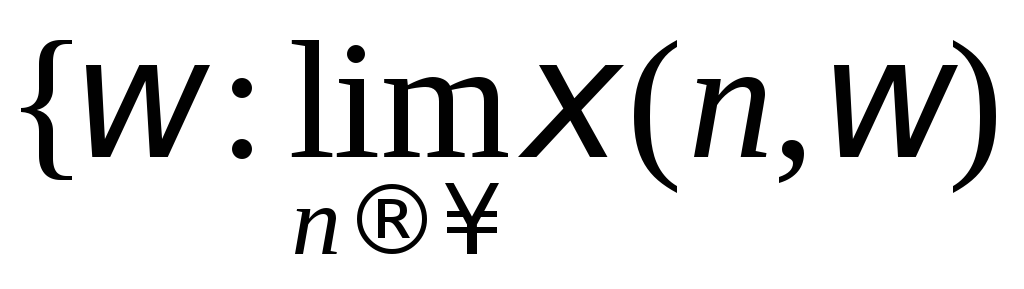 существует}? существует}? |
Будут
ли траектории случайного процесса
(t)
= 0t2
+ 1t
+2,
t
(a,
b),
непрерывны в обычном смысле почти
наверно на (a,b)? |
Будут
ли траектории случайного процесса
(t)
= 0t2
+ 1t
+2,
t
(a,b),
дифференцируемы в обычном смысле
почти наверно на (a,b)? |
Является
ли множество {:
Уравнение 0()t2
+ 1()t
+2()=0
имеет действительные корни} событием? |
Является
ли событием множество {:
Траектории процессов
 =0()t+0()
и =0()t+0()
и
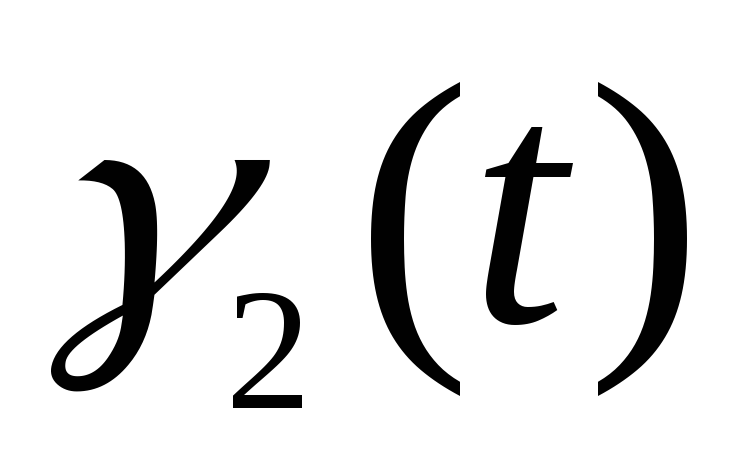 =1()t+1()
параллельны}? =1()t+1()
параллельны}? |
Является
ли событием множество {:
Траектории процессов
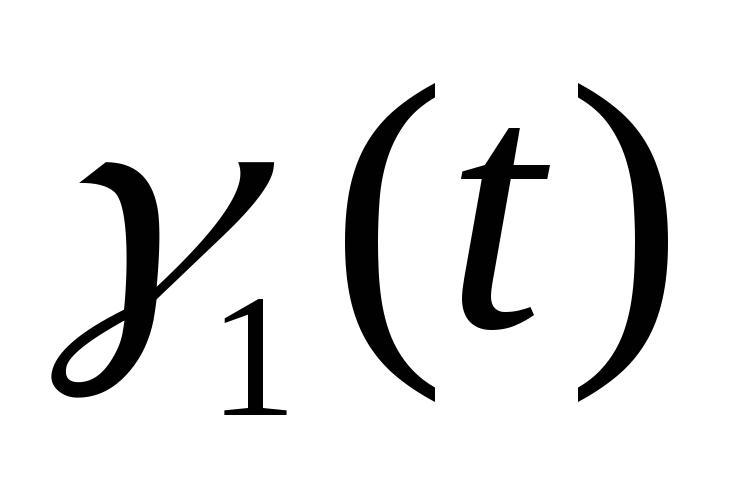 =0()t+0()
и =0()t+0()
и
 =1()t+1()
перпендикулярны}? =1()t+1()
перпендикулярны}? |
Пусть
случайные величины 1
и 2
равномерно распределены на отрезке
[-2;2] и независимы. Чему равна вероятность
Р(Траектории
процессов tg(1)t
и tg(2)t
образуют острый угол меньше 45)?
|
Пусть
случайная величина
равномерно распределена на отрезке
[-1;1]. Чему равна вероятность Р(Траектория
процесса t
образует с положительной полуосью
Ох
острый угол больше 60)?
|
Пусть
случайная величина
равномерно распределена на отрезке
[-1;1]. Чему равна вероятность Р(Траектория
процесса t
образует с положительной полуосью
Ох
угол по модулю меньше 60)?
|
Пусть
случайная величина
равномерно распределена на отрезке
[-1;1]. Чему равна вероятность Р(Траектория
процесса t
образует с положительной полуосью
Ох
угол по модулю меньше 30)?
|
Пусть
случайная величина
равномерно распределена на отрезке
[-1;1]. Чему равна вероятность Р(Траектория
процесса t
образует с положительной полуосью
Ох
угол по модулю больше 30)?
|
Пусть
случайная величина
имеет стандартное нормальное
распределение. Чему равно математическое
ожидание
 где где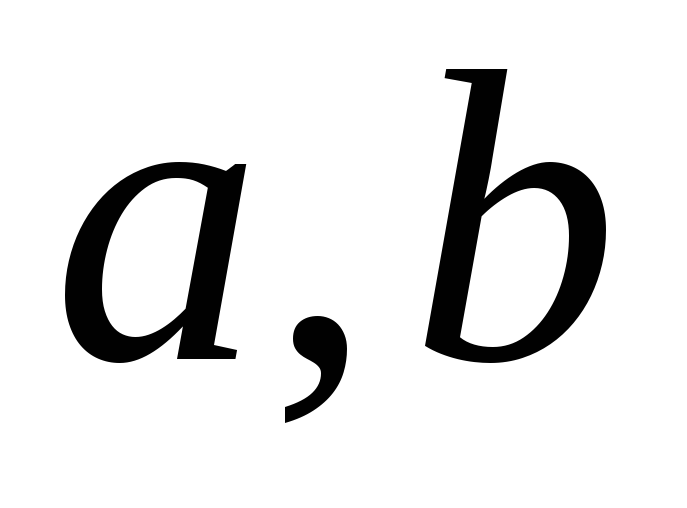 действительные
числа? действительные
числа? |
Пусть
случайные величины
и
независимы и имеют функции распределения
F
(x)
и F(y)
соответственно. Найти конечномерные
распределения (до порядка 3 включительно)
случайного процесса
 (t)=
t+. (t)=
t+. |
Пусть
случайные величины
и
независимы и имеют распределения:
– равномерное на [-1; 0] и
– равномерное на [0; 1]. Описать траектории
случайного процесса (t)=
t+. |
Пусть
случайные величины
и
независимы и имеют плотности
распределения р
(x)
и р
(y)
соответственно. Для процесса (t)=
t+
(1–t)
найти
плотность
 . . |
Пусть
и
независимы и имеют распределения:
– равномерное
на [-1,0] и
– равномерное
на [0,1]. Описать траектории случайного
процесса (t)=
t+. |

