
- •ОГЛАВЛЕНИЕ
- •ВВЕДЕНИЕ
- •ЛЕКЦИЯ 1. ПРЕДМЕТ ЭЛЕКТРОНИКИ. МАТЕРИАЛЫ ЭЛЕКТРОННОЙ ТЕХНИКИ И ИХ ЭЛЕКТРОФИЗИЧЕСКИЕ СВОЙСТВА
- •1.1. Введение.
- •1.2. Краткая история развития электроники.
- •ЛЕКЦИЯ 2. ЗОННАЯ ТЕОРИЯ ТВЕРДОГО ТЕЛА И СТАТИСТИКА НОСИТЕЛЕЙ ЗАРЯДА
- •2.1. Введение.
- •2.3. Обратная решетка.
- •2.6. Зоны Бриллюэна.
- •2.7. Плотность заполнения энергетических уровней в состоянии термодинамического равновесия.
- •ЛЕКЦИЯ 3. ЭЛЕКТРОПРОВОДНОСТЬ ВЕРДЫХ ТЕЛ
- •3.1. Электропроводность твердых тел.
- •3.2. Электропроводность металлов и диэлектриков.
- •3.5. Диффузия носителей заряда в полупроводниках.
- •ЛЕКЦИЯ 4. ЭЛЕКТРОННО-ДЫРОЧНЫЙ ПЕРЕХОД
- •ЛЕКЦИЯ 5. ПОЛУПРОВОДНИКОВЫЕ ДИОДЫ
- •5.1. Разновидности полупроводниковых диодов.
- •5.2. Выпрямительные полупроводниковые диоды. Характеристики и параметры. Влияние внешних условий на характеристики и параметры.
- •5.5. Стабилитроны: характеристики, параметры, применение.
- •ЛЕКЦИЯ 6. СТРУКТУРА И ПРИНЦИП ДЕЙСТВИЯ БИПОЛЯРНОГО ТРАНЗИСТОРА
- •6.1. Биполярные транзисторы.
- •6.2. Структура и принцип действия биполярного транзистора. Схемы включения (ОЭ, ОБ, ОК). Статические ВАХ и параметры для основных схем включения.
- •ЛЕКЦИЯ 7. АКТИВНЫЙ РЕЖИМ РАБОТЫ БИПОЛЯРНЫХ ТРАНЗИСТОРОВ
- •ЛЕКЦИЯ 8. КЛАССЫ УСИЛЕНИЯ
- •8.1. Понятие о классах усиления.
- •ЛЕКЦИЯ 9. ВЛИЯНИЕ ВНЕШНИХ УСЛОВИЙ НА ХАРАКТЕРИСТИКИ И ПАРАМЕТРЫ БТ
- •ЛЕКЦИЯ 10. ИСТОЧНИКИ ШУМОВ В БТ. МОДЕЛИ БТ
- •10.1. Источники собственных шумов в БТ.
- •ЛЕКЦИЯ 11. ТИРИСТОРЫ И СИМИСТОРЫ
- •11.1. Структура и принцип действия тиристоров и симисторов. Характеристики и параметры.
- •ЛЕКЦИЯ 12. ПОЛЕВЫЕ ТРАНЗИСТОРЫ
- •ЛЕКЦИЯ 13. МОП-ТРАНЗИСТОРЫ
- •13.1. Структура и принцип действия МОП-транзистора.
- •ЛЕКЦИЯ 14. ПРИМЕНЕНИЕ ПОЛЕВЫХ ТРАНЗИСТОРОВ
- •14.1. Основные схемы включения ПТ.
- •ЛЕКЦИЯ 15. МОДЕЛИ ПОЛЕВЫХ ТРАНЗИСТОРОВ
- •ЛЕКЦИЯ 16. ФОТОЭЛЕКТРИЧЕСКИЕ И ИЗЛУЧАТЕЛЬНЫЕ ПРИБОРЫ
- •16.1. Излучательная генерация и рекомбинация носителей заряда в полупроводниках под действием излучения.
- •16.2. Фотосопротивления, фотодиоды, фотоэлементы, фототранзисторы, фототиристоры, оптроны: характеристики, параметры, применение.
- •ЛЕКЦИЯ 17. ГЕТЕРОПЕРЕХОДЫ И ПРИБОРЫ НА ИХ ОСНОВЕ
- •17.1. Гетеропереходы. Зонная модель и инжекционные свойства гетеропереходов.
- •ЛЕКЦИЯ 18. ОСНОВЫ ТЕХНОЛОГИИ ПОЛУПРОВОДНИКОВЫХ ИНТЕГРАЛЬНЫХ СХЕМ
- •18.2. Технология полупроводниковых интегральных схем.
- •18.4. Эпитаксия.
- •18.5. Термическое окисление.
- •18.6. Легирование.
- •18.7. Травление.
- •ЛЕКЦИЯ 19. ПЛЕНОЧНЫЕ ТЕХНОЛОГИИ В ПРОИЗВОДСТВЕ ИНТЕГРАЛЬНЫХ СХЕМ
- •19.1. Нанесение тонких пленок.
- •19.2. Металлизация.
- •ЛЕКЦИЯ 20. ЭЛЕМЕНТЫ ИНТЕГРАЛЬНЫХ СХЕМ
- •20.1. Элементы интегральных схем.
- •ЛЕКЦИЯ 21. ЭЛЕМЕНТЫ ИНТЕГРАЛЬНЫХ СХЕМ (ОКОНЧАНИЕ)
- •21.1. Интегральные диоды.
- •21.3. МОП-транзисторы.
- •ЛЕКЦИЯ 22. БАЗОВЫЕ ЯЧЕЙКИ АНАЛОГОВЫХ ИНТЕГРАЛЬНЫХ СХЕМ
- •ЛЕКЦИЯ 23. БАЗОВЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ ЦИФРОВЫХ ИНТЕГРАЛЬНЫХ СХЕМ
- •23.1. Базовые логические элементы цифровых ИС на биполярных и полевых транзисторах.
- •ЛЕКЦИЯ 24. ЭЛЕКТРОВАКУУМНЫЕ ПРИБОРЫ И ОСНОВЫ ИХ РАБОТЫ
- •24.1. Классификация электровакуумных приборов.
- •ЛЕКЦИЯ 25. ПРИБОРЫ НА ОСНОВЕ АВТОЭЛЕКТРОННОЙ ЭМИССИИ
- •25.1. Приборы на основе автоэлектронной эмиссии.
- •ЛЕКЦИЯ 26. ПЕРСПЕКТИВЫ РАЗВИТИЯ ЭЛЕКТРОНИКИ. НАНОЭЛЕКТРОНИКА – НОВЫЙ ИСТОРИЧЕСКИЙ ЭТАП РАЗВИТИЯ ЭЛЕКТРОНИКИ
- •26.1. Перспективы развития электроники.
- •ЗАКЛЮЧЕНИЕ
- •БИБЛИОГРАФИЧЕСКИЙ СПИСОК

ЛЕКЦИЯ 2. ЗОННАЯ ТЕОРИЯ ТВЕРДОГО ТЕЛА И СТАТИСТИКА НОСИТЕЛЕЙ ЗАРЯДА
П л а н л е к ц и и
2.1. Введение.
2.2. Зонная теория твердого тела и статистика носителей заряда. 2.3. Обратная решетка.
2.4. Волновая механика свободных электронов.
2.5. Движение в пространстве с периодическим потенциалом. 2.6. Зоны Бриллюэна.
2.7. Плотность заполнения энергетических уровней в состоянии термодинамического равновесия.
2.8. Статистика носителей заряда в полупроводниках.
2.9. Зонная структура собственных и примесных полупроводников. 2.10. Зонная структура металлов и диэлектриков.
2.11. Генерация и рекомбинация носителей заряда в полупроводниках.
2.1. Введение.
Приведенный далее пример призван продемонстрировать принципиальную невозможность с позиций классической физики объяснить фундаментальные факты.
Размеры атома сегодня хорошо известны. Радиус среднего атома r ≈ 3 10–8 см. Положительно заряженое ядро держит отрицательно заряженный электрон с помощью силы кулоновского притяжения:
F = e2 |
/ r2 , |
(2.1) |
êóë |
|
|
где е – заряд электрона и протона. Чтобы атом был устойчив, силы притяжения недостаточно (электрон упал бы на ядро). Нужны уравновешивающие силы отталкивания. Такой силой является центробежная:
F = mυ2 |
/ r , |
(2.2) |
öá |
|
|
где m – масса электрона, V – его скорость. Равенство сил позволяет определить скорость электрона на круговой орбите:
V = (e2 / mr)1/ 2 . |
(2.3) |
Подставляя сюда численные значения для заряда, массы электрона и |
|
радиуса атома, получаем υ =106 м/с. Это огромная по |
земным и даже |
|
|
Электроника. Конспект лекций |
-21- |

ЛЕКЦИЯ 2. ЗОННАЯ ТЕОРИЯ ТВЕРДОГО ТЕЛА И СТАТИСТИКА НОСИТЕЛЕЙ ЗАРЯДА
2.1. Введение.
космическим масштабам скорость. Полная энергия электрона на орбите равна сумме потенциальной и кинетической энергий:
E = −e2 / 2r . |
(2.4) |
Знак минус означает, что за нуль энергии выбрана энергия электрона на бесконечном удалении от ядра.
Движущийся по орбите с ускорением электрон излучает энергию, при этом интенсивность излучения (эрг/с)
I = |
|
2e2r |
2 |
. |
(2.5) |
||
|
3C3 |
|
|||||
|
|
|
|
|
|||
Если каждую секунду электрон излучает I эргов, то за время |
|
||||||
τ ≈ |
r |
C 3 |
(2.6) |
||||
|
|
|
|
||||
υ |
|||||||
|
υ |
|
|||||
он растеряет всю свою энергию и упадет на ядро. Здесь τ – классическое время жизни электрона на орбите. Хотя оно значительно больше периода обращения электрона на орбите r/υ (так как C/υ значительно больше единицы), но все же чудовищно мало τ ≈ 10–10 c.
Это – лучшая демонстрация бессилия классической физики. Использование очевидных предпосылок, что невозможно существование стационарной структуры из заряженных частиц без движения и что частица, двигаясь с ускорением, излучает, приводит к тому, что атом существовать не может.
Чтобы ликвидировать это противоречие и была создана новая механика– квантовая. Квантовая механика (в отличие от классической – ньютоновской и релятивистской – эйнштейновской) создана не одним человеком, а целой плеядой замечательных физиков: Максом Планком, Нильсом Бором, Луи де Бройлем, Вернером Гейзенбергом, Эрвином Шредингером, Вольфгангом Паули, Полем Дираком, Энрико Ферми, Максом Борном. Именно квантовая механика позволяет объяснить закономерности поведения заряженных частиц внутри твердого тела.
2.2. Зоннаятеориятвердоготелаистатистиканосителейзаряда.
Одна из задач зонной теории твердого тела состоит в том, чтобы математически описать поведение заряженной частицы (например, электрона) в кристалле. Математическая модель при этом должна учитывать большинство эффектов, обусловленных влиянием кристаллической решетки.
Электроника. Конспект лекций |
-22- |

ЛЕКЦИЯ 2. ЗОННАЯ ТЕОРИЯ ТВЕРДОГО ТЕЛА И СТАТИСТИКА НОСИТЕЛЕЙ ЗАРЯДА
2.3.Обратная решетка.
2.3.Обратнаярешетка.
Важную роль для описания электронных свойств твердых тел играет понятие обратной решетки. На его основе можно решать задачи о распространении волн в кристаллах, а также дать определение энергетической зоны.
Обратная решетка – это упорядоченная совокупность точек, представляющая собой безразмерные значения волнового вектора,
нормированные к импульсу частицы: |
|
k = p/ . |
(2.7) |
Иногда ее называют решеткой в k пространстве или решеткой в пространстве волновых векторов.
Если некоторая плоская волна может быть описана выражением вида
Ψ = Ñ exp[ j(ωt −k r)], |
(2.8) |
то в общем случае при любом значении волнового вектора k период этой волны отличается от периода кристаллической решетки. Исключение составляют некоторые частные случаи, когда период волны совпадает с периодом кристаллической решетки. В таком случае говорят, что возникает обратная решетка с тем же законом периодичности, что и прямая решетка Бравэ.
2.4.Волноваямеханикасвободныхэлектронов.
В1924 г. по аналогии со световыми квантами Луи де Бройль высказал предположение, что любая частица (например электрон) должна обладать волновыми свойствами, и предложил формулу для определения длины волны, связанной с любой частицей (такую волну стали называть волной де Бройля):
λ = |
h |
, |
(2.9) |
|
p |
||||
|
|
|
где p – импульс частицы, h – постоянная Планка.
В 1926 г. Эрвин Шредингер вывел уравнение для описания волн де Бройля:
∂2Ψ(x) |
+ |
8π2m [E −V (x)]Ψ(x) = 0 , |
(2.10) |
∂x2 |
|
h2 |
|
Электроника. Конспект лекций |
-23- |

ЛЕКЦИЯ 2. ЗОННАЯ ТЕОРИЯ ТВЕРДОГО ТЕЛА И СТАТИСТИКА НОСИТЕЛЕЙ ЗАРЯДА
2.4. Волновая механика свободных электронов.
где Ψ(x)– волновая функция электрона; E – кинетическая энергия
электрона; V(x) – потенциальная энергия электрона; m – масса электрона. Максом Борном был показан вероятностный характер волновой
функции Ψ (обычно ее называют амплитудой вероятности). Величина Ψ 2 dυ называется функцией плотности вероятности, физический смысл
которой заключается в том, что она определяет вероятность существования частицы, описываемой волновой функцией Ψ в объеме dυ. Другими словами, вероятность существования электрона в объеме dυ определяется квадратом амплитуды его волновой функции. Соответствующая плотность
заряда −е Ψ 2 , где е – заряд электрона.
Согласно волновой механике между импульсом частицы и волновым
вектором существует соотношение |
|
p = k . |
(2.11) |
Здесь – постоянная Планка, деленная на 2π.
Кинетическая энергия свободного электрона определяется выражением
E = |
2k |
2 |
, |
(2.12) |
|
2m |
|
|
|
где m – масса электрона в свободном пространстве.
2.5. Движениевпространствеспериодическимпотенциалом.
Первым применением квантовой механики к рассмотрению движения электронов в твердых телах стала теория электропроводности металлов Зоммерфельда. В модели, названной моделью потенциального ящика (рис.
2.1), предполагалось, что в металле |
|
|
|
||||||
электроны |
внешних |
|
валентных |
|
|
|
|||
оболочек |
|
не |
принадлежат |
|
|
|
|||
определенным |
атомам, |
а |
могут |
|
|
V(x) |
|||
|
|
||||||||
свободно |
перемещаться |
по |
всему |
|
|
|
|||
|
|
|
|||||||
кристаллу. Считалось, что каждый |
|
|
|
||||||
электрон |
в |
металле |
движется |
в |
Рис. 2.1. Потенциальная энергия |
||||
пространстве, лишенном поля, так как |
электрона в металле. |
||||||||
силовые |
поля |
атомных |
|
остатков |
и |
Модель Зоммерфельда |
|||
|
|
|
|
||||||
всех остальных электронов, кроме данного, взаимно компенсируются везде, за исключением поверхности. У поверхности металла предполагалось существование поля, удерживающего электроны в объеме и затрудняющего выход электронов за его пределы.
Электроника. Конспект лекций |
-24- |

ЛЕКЦИЯ 2. ЗОННАЯ ТЕОРИЯ ТВЕРДОГО ТЕЛА И СТАТИСТИКА НОСИТЕЛЕЙ ЗАРЯДА
2.5. Движение в пространстве с периодическим потенциалом.
Ясно, что использованное в теории Зоммерфельда предположение, что электроны двигаются по металлу, не испытывая столкновений с атомами, является весьма грубым. Поэтому теория не дала объяснения существенному различию свойств металлов, диэлектриков и полупроводников.
Более правильный подход к рассмотрению движения электронов в твердом теле использован в модели Кронига – Пенни. В данной модели рассматривается движение электрона в пространстве периодически меняющегося потенциала, обусловленного положительными зарядами ядер, расположенными в узлах кристаллической решетки, и отрицательными зарядами электронов, окружающих эти положительные заряды.
Определим зависимость между энергией электрона и волновым вектором (или импульсом) в прямоугольном одномерном периодическом потенциале (рис. 2.2).
 V(x)
V(x)
V0
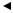 б
б
а
0 |
а+б |
2(а+б) |
3(а+б) |
х |
Рис. 2.2. Модель Кронига – Пенни
Уравнение Шредингера для этого случая запишем в виде
∂2Ψ(x) |
+ |
2m [E −V (x)]Ψ(x) = 0 , |
(2.13) |
∂x2 |
|
h2 |
|
где V(x) – периодический потенциал; Ψ(x) – волновая |
функция |
||
электрона.
Решения уравнения (2.13) являются функциями Блоха и имеют четкий физический смысл: это плоская волна с некоторым волновым числом k, промодулированная по амплитуде некоторой функцией U(x), также обладающая периодичностью решетки.
Ψ(x)=U (x)exp( jkx). |
(2.14) |
Подставляя уравнение (2.14) в ( 2.15) и решая его с учетом формы функции V(x), представленной на рис. 2.2, получаем зависимость между энергией Е и волновым вектором k, показанную на рис. 2.3.
Электроника. Конспект лекций |
-25- |

ЛЕКЦИЯ 2. ЗОННАЯ ТЕОРИЯ ТВЕРДОГО ТЕЛА И СТАТИСТИКА НОСИТЕЛЕЙ ЗАРЯДА
2.5. Движение в пространстве с периодическим потенциалом.
На графике рис. 2.3 в точках π/(a + b), где (a + b) соответствует
периоду потенциала Кронига – Пенни, появляются разрывы функции Е(k), т. е. возникают разрешенные и запрещенные энергетические зоны,
обозначенные цифрами 1 и 2 |
справа. Значения волнового вектора |
k = |
n π/(a + b), n = ±1, ±2,…, при |
которых возникает разрыв функции |
Е(k), |
удовлетворяют условию брэгговского отражения для электронной волны, падающей перпендикулярно на дифракционную решетку с периодом (a +b) .
(k)
− |
4π |
− |
3π |
− |
2π |
− |
π |
π |
|
2π |
|
3π |
|
4π |
|
|
a +b |
|
a +b |
|
a +b |
|
a +b |
|
a +b |
|
a +b |
|
a +b |
|
a +b |
Рис. 2.3. Зависимость энергии E(k) электрона от волнового вектора k в потенциале Кронига – Пенни (сплошная линия). Пунктирной линией показана зависимость E(k)
для свободного электрона: 1 – разрешенная зона; 2 – запрещенная зона
Для сравнения на рис. 2.3 пунктирной линией показана функция Е(k) для свободного электрона в соответствии с выражением (2.12). Видно, что функция Е(k) для свободного электрона и электрона в периодическом потенциале подобны. Поведение свободного электрона соответствует частному случаю, если в функции Блоха (2.14) U(x) = const. Поэтому можно принять, что по аналогии с моментом импульса свободного электрона для электрона в периодическом потенциале (или в кристаллической решетке) существует некоторый момент, называемый моментом кристалла.
Электроника. Конспект лекций |
-26- |
