4. Властивості рідин

4.1.Особливості поверхневого шару рідини

Найбільш характерною властивістю рідкого стану є наявність різкої межі, яка розділяє рідину та її пару.

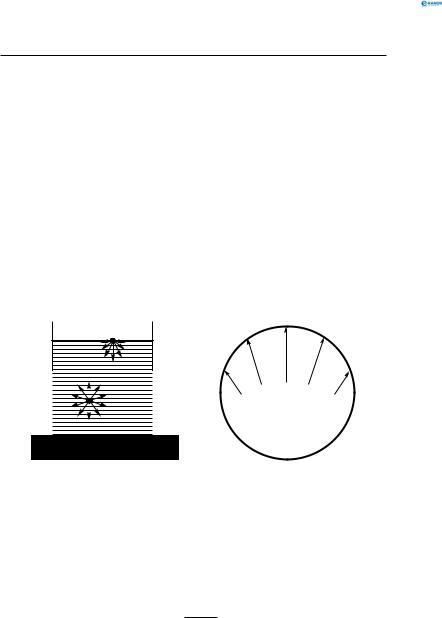
Молекули рідини, що містяться на її поверхні, притягуються молекулами, які є всередині рідини. Притягання молекул пари, які містяться над поверхнею, є мізерно малим. Під впливом рівнодійної сили притягання молекули поверхневого шару втягуються всередину рідини, кількість молекул на поверхні зменшується, і площа поверхні скорочується. На поверхні залишається така кількість молекул, при якій її площа виявляється мінімальною для даного

об’єму рідини (рис. 136, а).

Сила поверхневого натягу — це сила, яка діє на межі стикання рідини з твердим тілом перпендикулярно до межі по дотичній до поверхні рідини (рис. 136, б).

Рис. 136

4.2. Поверхнева енергія. Поверхневий натяг

Поверхневим натягом називається величина, вимірювана відношенням модуля сили поверхневого натягу до довжини межі поверхні плівки:

σ = Fн .

lмежі

У СІ поверхневий натяг виражається в ньютонах на

165

Молекулярна фізика

Величина поверхневого натягу залежить від виду рідини і температури.

Енергія поверхневого шару рідини площею S:

П = σS .

Робота при зміні площі поверхневого шару плівки:

A = σ∆S = ∆П .

Величину поверхневого натягу можна визначити мето-

дом відриву крапель:

σ = mlкg ,

де mк — маса краплі;

g — прискорення вільного падіння;

l — довжина межі поверхневого шару.

4.3. Явище змочування. Капілярні явища

Рідина, яка розтікається по твердому тілу, називається змочуючою дане тверде тіло (вода по склу і т. п.). При цьо-

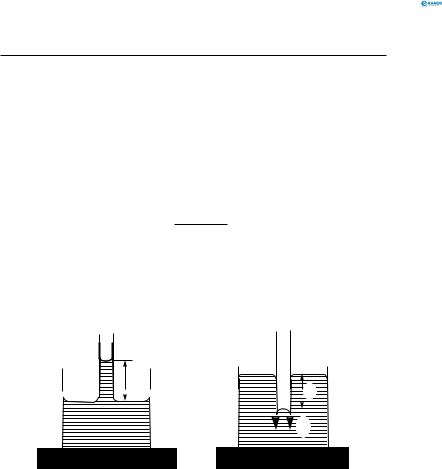
му рівнодійна сил притягання молекул на межі зіткнення з молекулами рідини менша, ніж з молекулами твердого тіла

(рис. 137, а).

Рідина, що не розтікається, а стягується міжмоле­ кулярними силами в краплі, називається незмочую-

чою дане тверде тіло (вода на жирній поверхні і т.  п.). Рівнодійна сила притягання молекул на межі зіткнення з молекулами рідини більша, ніж з молекулами твердого тіла (рис. 137, б).

Рис. 137

166

4. Властивості рідин

θ — крайовий кут.

Якщо повне змочування, θ =0.

Якщо повне незмочування, θ = π.

Змочування — це трифазне явище, оскільки воно відбувається на межі трьох фаз: твердої, рідкої і газоподібної.

У тонкій трубці — капілярі — у разі змочування рідина піднімається по стінці, утворюється ввігнута поверхня рідини (увігнутий меніск) (рис. 138, а).

Висота підйому рідини в трубці:

h = 2σcosθ .

ρgr

де σ — поверхневий натяг; r — радіус трубки;

ρ — густина рідини.

Незмочуюча рідина опускається в капілярі на h, меніск при цьому є опуклим (рис. 138, б).

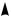
F

F

Рис. 138

4.4. Формула Лапласа

Формула Лапласа

Додатковий тиск, який зумовлений кривиною поверхні рідини, визначається так:

де R1 і R2 — радіуси кривини двох взаємно перпендикулярних перетинів поверхні рідини; знак «+» — для опуклого меніска, «–» — увігнутого.

167

Молекулярна фізика

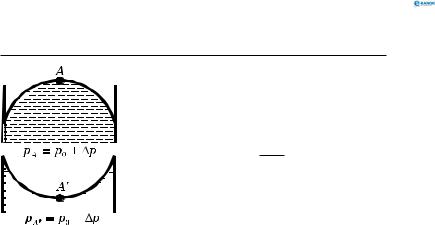
Тиск у точках A і A′ зазначений на рис. 139:

p0 — тиск на вільну поверхню. Якщо R1 = R2 = R (сферична по-

верхня), то

∆p =

4.5. Приклади розв’язання задач

Задача 1.

Корковий кубик із ребром 2 см плаває у воді. Визначи­ ти глибину його занурення у воду, вважаючи змочування повним.

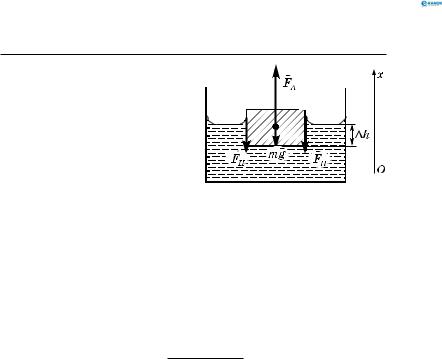
Оскільки кубик перебуває у рівновазі, то геометрична сума сил, діючих на кубик, дорівнює нулю (рис. 140):

168

4. Властивості рідин

Виразимо шукану глибину занурення кубика в рідину ∆h :

Скорочуючи на a чисельник і знаменник виразу (2), дістанемо:

∆h = ρпр ga2 +4σ .

ρрідga

Відповідь: ∆h =0,62 см.

Задача 2.

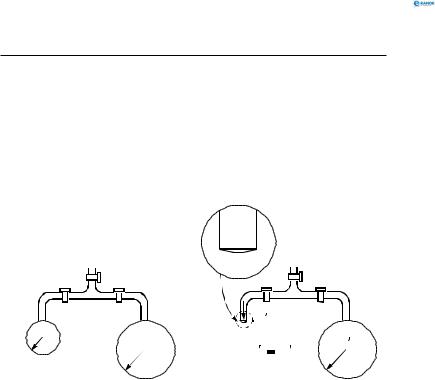
На протилежних кінцях трубки-трійника видули дві мильні бульбашки A і B різних діаметрів, після чого вихідний отвір трубки закрили (рис. 141). Що станеться з буль­башками, якщо залишити їх самих, захистивши від зовнішніх впливів (відкрити крани 1 і 3)?

Аналіз і розв’язання:

Об’єм бульбашки A зменшуватиметься, а об’єм бульбашки B — збільшуватиметься, оскільки лапласів тиск

169

Молекулярна фізика

му радіусу відповідає менший лапласів тиск).

Рівновага настане, коли тиск eсередині бульбашок (лапласові тиски) зрівняється, тобто коли поверхні обох плівок (радіус кульового сегмента першої плівки R1′ і радіус кулі другої плівки R2′ ) матимуть однакову кривину: R1′ = R2′

(рис. 142).

Задача 3.

Під час посухи на поверхні землі утворюється тверда кірка. Чи треба зберігати її, щоб запобігти висиханню нижніх шарів землі?

Аналіз і розв’язання:

Ні, ґрунт слід розрихлювати, щоб перешкодити підйому ґрунтової води по капілярах, які утворюються у верхніх затверділих шарах ґрунту.

Задача 4.

У капілярній трубці, зануреній вертикально у воду на глибину l, вода піднялась на висоту h (рис. 143). Трубку закривають знизу пальцем, виймають із води і знову відкривають. Визначити довжину x стовпчика води, який залишився в трубці. Кривину верхнього ввігнутого і нижнього опуклого менісків вважати однаковою.

170

4. Властивості рідин

Лапласів тиск дорівнює гідростатичному тиску стовпчика рідини заввишки h. Коли трубку виймаємо з води, утворюється два меніски. Лапласів тиск збільшується, а отже, збільшується висота стовпчика води в капілярі. Визначимо цю висоту. Коли трубку відкриваємо, вода з капіляра виливається доти, поки внизу не утвориться опуклий меніск. Лапласів тиск напрямлений угору і дорівнює:

pл = pл1 + pл2;

а) якщо l > h , то (рис. 144, а)

pл =2pл =ρgx1 ,  2ρgh =ρgx1 , x1 =2h ;

б) якщо l < h , то (рис. 144, б)

171

Молекулярна фізика

pл1 + pл2 =ρgx2 , ρgh +ρgl =ρgx2 , x2 =l +h .

Відповідь: x1 =2h , якщо l > h ; x2 =l +h, якщо l < h.

Задача 5.

Яку роботу треба виконати, щоб розтягнути на відстань d = 10 см мильну плівку на дротяній рамці з рухомою перекладиною завдовжки l = 5 см?

Розв’язання:

Робота A дорівнює збільшенню енергії вільної поверхні рідини:

Оскільки треба враховувати збільшення поверхні з обох боків плівки, то ∆S =2dl .

Тоді A =2σdl .

Обчислення:

A = Нм м м = Н м = Дж ,

{ A} =2 40 10−3 0,1 5 10−2 =4 10−4 .

Відповідь: A = 400 мкДж.

Задача 6.

Яка кількість теплоти виділиться в навколишнє середо­ вище, якщо при злитті крапельок діаметром 1 мкм вийде 1 кг чистої води при тій самій температурі? На скільки градусів нагрілась­ би вода, якби не було тепловіддачі?

172

Розв’язання:

Краплі, порівняно з водою, яка міститься в одній посудині, мають значно більшу поверхневу енергію. Ця надлишкова енергія

ди, якби не було теплообміну з навколишнім середовищем.

173

Молекулярна фізика

Згідно із законом збереження енергії Q = П, тоді

Відповідь: ∆t = 0,1°C , ∆T = 0,1К .

Задача 7.

Яку роботу проти сил поверхневого натягу треба виконати, щоб видути мильну бульбашку радіусом R? Чому дорівнює надлишковий тиск усередині бульбашки?

Розв’язання:

Мильна бульбашка являє собою дуже тонку плівку мильної води приблизно сферичної форми. Ця плівка має дві поверхні — зовнішню і внутрішню. Нехтуючи товщиною плівки і вважаючи тому радіуси обох сфер однаковими, знайдемо їхню спільну площу:

Збільшення поверхневої енергії пов’язане зі збільшенням ∆S :

Виконувана під час видування бульбашки робота проти сил поверхневого натягу іде на збільшення поверхневої енергії на ∆П. Таким чином, із (1) і (2) дістанемо:

A = ∆П =8πR2σ .

Надлишковий (порівняно із зовнішнім) тиск усередині бульбашки дорівнює:

∆p = 4Rσ .

174