
Lineynaya algebra i analitich_geom / Resheniya_zadach_po_kuznecovu_lineynaya_algebra_izdanie_2011
.pdfx' |
1 |
4 |
3 |
6 |
15 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
y' |
|
1/ 3 |
7 / 3 |
2 |
|
3 |
|
|
7 |
, |
|
|
|
|
4 / 3 |
16 / 3 |
5 |
|
1 |
|
|
19 |
|
z' |
|
|
|
|
|
||||||
значит координаты x {6,3,1}относительно базиса {e1' , e2' , e3' } будут {15, 7, 19}.
Задача 5. Пусть x (x1 , x2 , x3 ) . Являются ли линейными следующие преобразования:
Ax (6x1 5x2 4x3 ,3x1 2x2 x3 , x2 ), Bx (6x1 5x2 4,3x1 2x2 x3 , x2 ), Cx (6x1 5x2 4x33 ,3x1 2x2 x3 ,0).
Здесь линейным преобразованием будет преобразование А, т. к. при линейном преобразовании координаты получившегося вектора будут линейными комбинациями координат исходного вектора.
Матрица линейного оператора А:
6 |
5 |
4 |
|
|
|
|
|
|
|
А |
3 |
2 |
1 |
. |
|
0 |
1 |
0 |
|
|
|
|||
Задача 6. Пусть x {x1 , x2 , x3}, Ax {x2 x3 , x1 , x1 x3}, Bx {x2 ,2x3 , x1}. Найти:
B2 A x.
X {x1 ; x2 ; x3}, Ax {x2 x3 ; x1; x1 x3}, Bx {x2 ;2x3 ;x1}
|
|
|
0 |
1 0 |
|
0 |
|
1 0 |
|
0 0 |
2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
B 2 B B |
0 |
0 2 |
|
|
0 |
|
0 2 |
|
|
2 0 |
0 |
, |
||||||||||||||||
|
|
|
|
1 |
0 0 |
|
|
|
1 |
|
0 0 |
|
|
|
0 1 |
0 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
0 |
|
0 |
2 |
|
0 1 |
1 |
|
0 1 |
|
1 |
|||||||||||||||||
B 2 A |
|
2 |
|
0 |
0 |
|
|
|
1 0 |
|
0 |
|
|
3 0 |
|
0 |
, |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
0 |
|
1 |
0 |
|
|
|
1 0 |
|
1 |
|
|
|
1 1 |
|
1 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
0 |
1 1 x |
|
|
x |
|
x |
|
|
|
|
|
||||||||||||||
(B 2 A)x |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
|||
|
3 |
0 0 |
|
|
x |
2 |
|
|
|
|
|
3x |
|
|
|
, |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||||
|
|
|
1 |
1 1 |
x |
3 |
|
|
x x |
2 |
x |
3 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||||
т.е. B2 A x {x2 x3 ;3x1 ; x1 x2 x3}.
Задача 7. Найти матрицу линейного оператора в базисе (e1 ', e2 ', e3 ') , где
e1 ' e1 e2 e3 , e2 ' e1 e2 2e3 , e3 ' e1 2e2 e3 , если она задана в базисе
(e1 , e2 , e3 ) .
А'?, A' T 1 A T

2 0 |
1 |
1 |
1 |
1 |
||||
|
|
|
|
|
|
|
|
|
A |
0 |
1 |
1 |
, Т |
1 |
1 |
2 |
. |
|
1 |
1 |
1 |
|
1 |
2 |
1 |
|
|
|
|
|
|
|
|
|
|
Найдем Т 1 . |
|
|
|
|
|
|
|
||||
|
1 |
1 |
|
5 |
3 |
1 |
|
||||
|
1 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Т |
|
1 |
1 |
2 |
|
1, T 1 |
3 |
2 |
1 |
. |
|
|
|
1 |
2 |
1 |
|
|
1 |
1 0 |
|
|
|
|
|
|
|
|
||||||
5 |
3 |
1 2 0 |
1 1 |
1 |
1 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
A' |
3 |
2 |
1 |
|
0 |
1 |
1 |
1 |
1 |
2 |
|
|
|
1 |
1 |
0 |
|
1 |
1 |
|
1 |
2 |
1 |
|
|
|
|
1 |
|
|
||||||||
11 |
4 |
1 1 |
1 |
1 |
6 |
5 |
4 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
3 |
0 |
|
1 |
1 |
2 |
|
|
4 |
4 |
1 |
. |
|
2 |
1 |
0 |
|
1 |
2 |
1 |
|
|
1 |
1 0 |
|
|
|
|
|
|
|
|||||||||
|
|
6 |
5 |
4 |
|
|
Значит матрица в базисе {e1' , e2' |
, e3' |
|
|
4 |
|
|
} имеет вид |
4 |
1 |
. |
|||
|
|
|
1 |
1 |
0 |
|
|
|
|
|
|||
Задача 8. Доказать линейность, найти матрицу (в базисе i, j, k ), образ и ядро оператора
поворота относительно оси Oz в положительном направлении на угол  2 .
2 .
Если x {x1 , x2 , x3 }, то Ax {x2 ,x1 , x3 } .
Оператор является линейным, если
A x Ax и A(x y) Ax Ay .
x (x1 ; x2 ; x3 ) A( x) (x2 ;x1 ; x3 ) Ax . x y {x1 y1 ; x2 y2 ; x3 y3}.
A(x y) {x2 y2 ;x1 y1 ; x3 y3}.
0 |
1 |
0 |
|
|
|
|
|
|
|
Т.е. оператор А является линейным и его матрица A |
1 |
0 |
0 |
. |
|
0 |
0 |
1 |
|
|
|
|||
Область значений оператора А — это множество всех векторов y Ax {x2 ;x1 ; x3}.
Ядро линейного оператора — множество векторов, которые А отображает в нуль-вектор:
KerA {0;0;0}.
Задача 9. Найти собственные значения и собственные векторы матрицы.
2 |
1 |
0 |
|
|
|
1 |
|
|
|
|
2 |
0 |
. |
|
|
1 |
1 |
1 |
|
|
|
|||
Составляет характеристическое уравнение и находим его решение.
|
2 |
1 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
2 |
|
0 |
|
0, |
|
|
|
|
|
|
|
1 |
1 |
1 |
|
|
|
|
|
|
|||
(2 )(2 )(1 ) (1 ) 0, |
|
|||||||||||
(1 )(2 |
4 3) 0, |
|
|
|
|
|
||||||
( 1)2 ( 3) 0. |
|
|
|
|
|
|||||||
Собственные значения: 1,2 |
1, 3 3. |
|||||||||||
Найдем собственные вектора. |
|
|
|
|
||||||||
|
|
|
x |
x |
|
0 |
|
x |
C |
|
||
1,2 1 |
|
1 |
|
2 |
|
|
|
|
1 |
1 |
||
, x1 x2 0 |
x2 C1 ; |
|||||||||||
|
|
|
x |
x |
2 |
0 |
|
x |
3 |
C |
2 |
|
|
|
|
1 |
|
|
|
|
|
|
|||
|
|
|
x1 x2 0 |
|
|
x1 C1 |
|||||||||
3 3 |
|
x1 |
x2 0 |
|
|
|
C1 . |
||||||||
, |
x2 |
||||||||||||||
|
|
x x |
2 |
2x |
3 |
0 |
|
|
x |
3 |
C |
||||
|
|
|
1 |
|
|
|
|
|
|
|
1 |
||||
Собственные вектора: |
|
|
|
|
|
|
|
||||||||
|
|
1 |
|
|
|
|
0 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X1 |
|
1 |
, X 2 |
|
0 |
, X |
3 |
|
1 . |
|
|
||||
|
|
0 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Задача 10. Привести квадратичную форму к каноническому виду методом Лагранжа.
4x12 8x1x2 4x1x3 3x22 2x32.
4x12 8x1 x2 4x1 x3 3x22 2x32 (2x1 )2 2 2x1 2x2 2 2x1 x32 2x2 x3 (2x2 )2 x32 x22 x32 (2x1 2x2 x3 )2 x22 x32
y12 y22 y32 ,
где y1 2x1 2x2 x3 , y2 x2 , y3 x3 .
Задача 11. Привести квадратичную форму к каноническому виду ортогональным преобразованием.
x2 |
x2 |
3x2 |
2x x 6x x 6x x . |
|||||||||
1 |
|
2 |
3 |
|
1 |
2 |
1 |
3 |
2 |
3 |
||
|
|
1 |
1 |
|
3 |
|
|
|
|
|
|
|
|
А |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
3 , |
|
|
|
|
|
||||
|
|
|
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
||
|
1 |
1 |
|
3 |
|
(1 )2 ( 3 ) 9 9 9(1 ) |
||||||
|
|
|
||||||||||
|
1 |
|
1 |
|
3 |
|
||||||
|
3 |
|
3 |
|
3 |
|
|
|
|
|
||
9(1 ) (3 ) 3 |
|
52 |
12 36. |
|||||||||
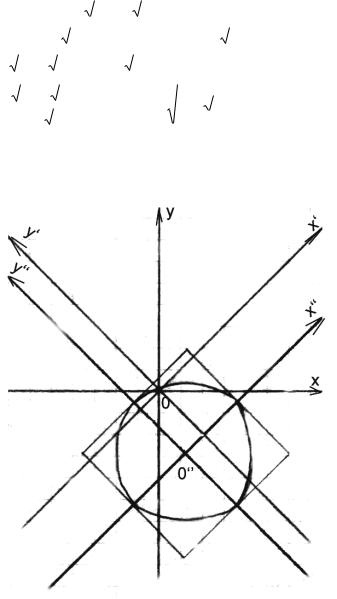
Задача 12. Исследовать кривую второго порядка и построить ее.
3x2 3y 2 4xy 8x 12y 1 0.
x x'cos y'sin ,y x'sin y'cos
|
|
|
|
|
|
|
|
|
|
|
|
a12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
tg 2 |
|
|
|
|
|
|
|
|
|
|
|
, 4 . |
|
|
|
|
|
|
|
|
|||||||||||
|
a |
|
|
a |
22 |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
3(x'cos y'sin )2 |
3(x'sin y'cos )2 4(x'cos y'sin )(x'sin y'cos ) |
||||||||||||||||||||||||||||||
8(x'cos y'sin ) 12(x'sin y'cos ) 1 0, |
|||||||||||||||||||||||||||||||
x'2 (3 4 cos sin ) y'2 |
(3 4 sin cos ) 4x' y'(cos 2 sin 2 ) |
||||||||||||||||||||||||||||||
x'(8 cos 12 sin ) y'(12 cos 8sin ) 1 0. |
|||||||||||||||||||||||||||||||
5x'2 y'2 10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
2x' 2 |
|
2 y' 1 0, |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
(5x'2 2 |
|
|
|
2 5x' 2) 2 ( y'2 2 |
|
2 y' 2) 2 1 0, |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
( 5x' 2)2 ( y' 2)2 3, |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
5x' |
2 x'', |
|
|
|
|
2 |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
0'' |
|
; 2 |
, |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
y' 2 |
y'' |
|
|
|
|
|
5 |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x'' |
|
y'' |
|
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||






