
- •Производная. Определение, непрерывность функции, имеющей производную.
- •Геометрический смысл производной.
- •Арифметические свойства производной.
- •Производная обратной функции.
- •Производная сложной функции.
- •Производные элементарных функций.
- •Билет 7 Дифференциал функции. Определение. Геометрический смысл.
- •Необходимое и достаточное условие дифференцируемости.
- •Теорема 1: Для того, чтобы функция была дифференцируемой в точке, необходимо и достаточно , чтобы она имела конечную производную в этой точке.
- •Производные высших порядков. Формула Лейбница.
- •Дифференциалы высших порядков. Инвариантность формы первого дифференциала. Неинвариантность формы дифференциалов второго и высших порядков.
- •Возрастание (убывание) функции в точке. Необходимое и достаточное условие. Теорема Ферма.
- •Теорема Ролля.
- •Теорема Коши. Физический смысл.
- •Теорема о среднем Лагранжа.
- •Достаточное условие невозрастания (неубывания) функции на отрезке. Условие постоянства функции на отрезке.
- •Достаточные условия экстремума.
- •Формула Тейлора для многочленов.
- •Формула Тейлора для дифференцируемых функций.
- •Формула Тейлора для важнейших элементарных функций.
- •Билет 20 Выпуклость функции в точке. Достаточное условие.
- •Теорема 1 (Достаточное условие существования точки перегиба).
- •Непрерывна в и. Тогда, если- нечетное число, то криваяобращена выпуклостью вверх или вниз в зависимости от того, будет лиили, а есличетное, тоесть точка перегиба кривой.
- •Выпуклость функции на отрезке. Необходимое и достаточное условие.
- •Правило Лопиталя. Случай 0/0.
- •1) A – конечное.
- •Правило Лопиталя. Случай .
- •Раскрытие неопределенностей вида ,,,,.
- •Асимптота. Уравнение наклонной асимптоты.
- •Первообрáзная. Неопределенный интеграл. Свойства.
- •Замена переменной в неопределенном интеграле.
- •Интегрирование по частям неопределенного интеграла.
- •Интегрирование простейших рациональных дробей
- •Интегрирование рациональных дробей.
- •Интегрирование выражений вида.
- •Первая подстановка Эйлера (Леонарда)
- •Интегрирование тригонометрических выражений.
- •Тригонометрические подстановки.
- •Определенный интеграл Римана. Эквивалентные определения. Условие Коши.
- •Ограниченность интегрируемой функции.
- •Суммы Дарбу. Их Свойства.
- •Суммы Дарбу и интегрируемость функции по Риману.
- •Билет 41 Основная теорема о существовании определенного интеграла Римана.
- •Равномерная непрерывность функции. Модуль непрерывности.
- •Теорема 2 Функция непрерывная на отрезке, равномерно непрерывна на нем ().
- •Интегрируемость по Риману непрерывной функции.
- •Интегрируемость по Риману монотонной функции.
- •Аддитивное и однородные свойства определенного интеграла Римана.
- •Неравенства для определенного интеграла Римана и теорема о среднем.
- •Интеграл как функция верхнего предела. Непрерывность и дифференцируемость. Теорема Ньютона-Лейбница.
- •Билет 48 Определение площади. Площадь криволинейной трапеции. Площадь в полярных координатах.
- •Определение объёма. Объем тела вращения.
- •Длина дуги кривой. Определение и вычисление.
Интегрирование по частям неопределенного интеграла.
Пусть даны U и V, тогда по правилу интегрирования по частям
![]()

Пример 1:
![]()
Пример 2:

![]()
Пример 3:

Пример 4:

Правило:
При интегрировании
выражений вида
![]() ,
гдеP(x)-многочлен,
,
гдеP(x)-многочлен,
Если
![]() заU
принимаем
заU
принимаем
![]()
Если
![]() заU
принимаем
заU
принимаем
![]()
Пример5.

![]()
![]()
![]()
Билет 30
Интегрирование простейших рациональных дробей
1.![]()
2.![]()
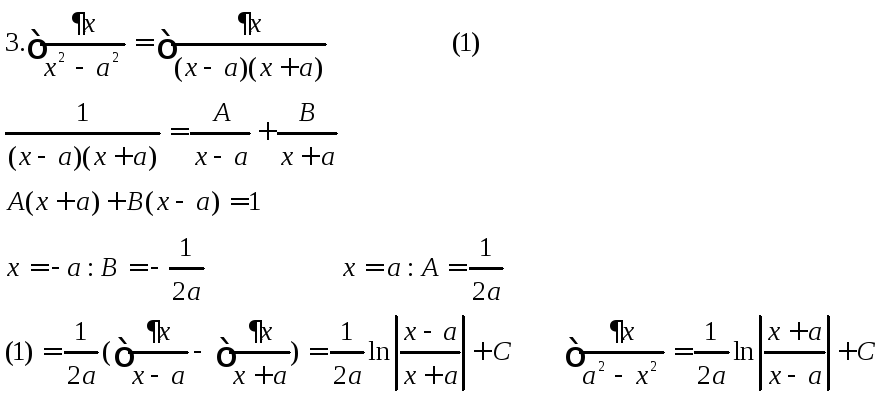
4.

5 .
.
рассмотрено в пункте 3
рассмотрено в пункте 4.
6. 
7.
8. -случай
7
-случай
7
9. Случай
8.
Случай
8.
Билет 31
Интегрирование рациональных дробей.
Пусть
нужно найти неопределенный интеграл
![]() от рациональной действительной дроби.
Если степень многочленаP
k
не меньше степени многочлена Q
n
(
от рациональной действительной дроби.
Если степень многочленаP
k
не меньше степени многочлена Q
n
(![]() ),
то прежде всего разделим P
на Q
:
),
то прежде всего разделим P
на Q
:
![]()
Многочлен
R
интегрируется без труда, а
![]() – правильная действительная дробь. Все
трудности сводятся к интегрированию
правильной дроби, которую мы снова
обозначим через
– правильная действительная дробь. Все
трудности сводятся к интегрированию
правильной дроби, которую мы снова
обозначим через![]() и
представим в виде:
и
представим в виде:
![]()
Тогда
пусть
![]() ,
,
![]()
1 случай.
Знаменатель содержит простые действительные корни, тогда его можно разложить на простейшие множители: (см.Теор.1)
![]() .
Тогда
.
Тогда
![]()
Приравнивая тождественно равные числители, получим:
![]()
Существуют
2 метода нахождения
![]() :
:
сравниваем коэффициенты при x с одинаковыми степенями; однако этот метод очень трудоемкий.
Т.к. равенства тождественны, можем взять
 ,
тогда
,
тогда .
Так, подставляя поочередно
.
Так, подставляя поочередно найдем все
найдем все
Т.о., мы получили сумму элементарных дробей, которые можем легко проинтегрировать.
Пример
![]()
2 случай.
Знаменатель содержит кратные корни, тогда его можно представить в виде:
![]() .
.
Пусть
существуют n
различных корней с кратностями
![]() ,
тогда
,
тогда
![]() - и делаем все
так же, как и в предыдущем примере.
- и делаем все
так же, как и в предыдущем примере.
Пример
![]()
3 случай.
Знаменатель содержит кратные корни и многочлены, имеющие комплексные корни;
![]() ,
где многочлены
,
где многочлены
![]() ,
,![]() имеют комплексные корни.
имеют комплексные корни.
Тогда R(x) представим в виде:
![]()
Снова приводим к общему знаменателю и приравниваем числители.
Пример
![]()
4 случай
Знаменатель содержит кратные действительные и кратные комплексные корни;
![]()
Тогда R(x) представим в виде:
![]()
А дальше все делаем по старой схеме: методом неопределенных коэффициентов находим A, B...
Пример
![]()
Теорема 1
Любой многочлен над полем С раскладывается на линейные и квадратичные множители с действительными коэффициентами:

Доказательство
Если
![]() ,
то все в порядке:
,
то все в порядке:![]() - линейный множитель с вещественными
коэффициентами
- линейный множитель с вещественными
коэффициентами
Пусть
тогда существует невещественный корень
![]() .
Ему соответствует скобка
.
Ему соответствует скобка![]() .
.
Тогда
если
![]() – корень, то сопряженный к нему
– корень, то сопряженный к нему![]() тоже будет корнем. Тогда наряду с
множителем
тоже будет корнем. Тогда наряду с
множителем![]() будет присутствовать множитель
будет присутствовать множитель![]() .
Перемножим эти 2 скобки:
.
Перемножим эти 2 скобки:![]() - квадратный трехчлен с вещественными
коэффициентами, что и требовалось
доказать.
- квадратный трехчлен с вещественными
коэффициентами, что и требовалось
доказать.
Теперь нам нужно доказать, что любые правильные дроби раскладываются на простейшие.
Лемма 1
Пусть
многочлен
![]() представим в виде:
представим в виде:![]() ,
где
,
где![]() -
выделили максимальное кол-во скобок
(x-a)
-
выделили максимальное кол-во скобок
(x-a)
и
![]() - степень числителя меньше степени
знаменателя, тогда
- степень числителя меньше степени
знаменателя, тогда
![]() ,
причем дробь
,
причем дробь
![]() -
правильная; если
-
правильная; если![]() ,
то
,
то![]() ;M(x)
– многочлен с действительными
коэффициентами.
;M(x)
– многочлен с действительными
коэффициентами.
Доказательство
Действуем так же, как в примерах: приводим к общему знаменателю и приравниваем числители:
![]() ;
подставим
;
подставим
![]() ,
тогда
,
тогда![]() ,
по условию
,
по условию![]()
![]() - нам нужно доказать,
что это – многочлен, а не дробь. Подставим
x=a,
числитель при такой подстановке = 0, а
это значит, что многочлен
- нам нужно доказать,
что это – многочлен, а не дробь. Подставим
x=a,
числитель при такой подстановке = 0, а
это значит, что многочлен
![]() делится на
делится на![]() ,
т.е.M(x)
– многочлен с действительными
коэффициентами.
,
т.е.M(x)
– многочлен с действительными
коэффициентами.
Теперь
докажем, что дробь
![]() - правильная, т.е. что
- правильная, т.е. что![]() .
.
Степень
знаменателя дроби = n-1,
для числителя ( M(x)):
по условию
![]() и
и![]()
![]() ,
да еще делим на (x-a)
(
,
да еще делим на (x-a)
(![]() ),
значит
),
значит![]() - меньше степени знаменателя, что и
требовалось доказать.
- меньше степени знаменателя, что и
требовалось доказать.
Лемма 2
Если
многочлен Q(x)
имеет комплексный корень кратности k,
т е представим в виде
![]() ,
при этом многочлен
,
при этом многочлен![]() имеет только комплексные корни, которые
не являются корнямиN(x).
имеет только комплексные корни, которые
не являются корнямиN(x).
![]() ,
тогда дробь можно представить в виде:
,
тогда дробь можно представить в виде:
![]() ,
причем вторая дробь будет правильной.
M(x)
– многочлен с действительными
коэффициентами.
,
причем вторая дробь будет правильной.
M(x)
– многочлен с действительными
коэффициентами.
Доказательство
Снова
приведем дробь к общему знаменателю и
приравняем числители. Получим
![]()
Пусть
![]() ,
,![]() -
корень многочлена
-
корень многочлена![]() ,
,![]() ,
значит сопряженное к нему
,
значит сопряженное к нему![]() тоже
корень. Подставим
тоже
корень. Подставим![]() и
и![]() :
:
![]()
![]()
![]() ;
;![]()
![]()
![]() Найдем определитель системы, чтобы
выяснить, имеет она решения, или нет:
Найдем определитель системы, чтобы
выяснить, имеет она решения, или нет:
![]() ,
значит, система разрешима и существуют
A
и B
– решения системы, нужно доказать, что
,
значит, система разрешима и существуют
A
и B
– решения системы, нужно доказать, что
![]()
![]() ,
заменим A
и B
на
,
заменим A
и B
на
![]() :
:![]() ,
решим сопряженную систему:
,
решим сопряженную систему:![]() - получили исходную систему;
- получили исходную систему;
так
как столбец
![]() -
решение, столбец
-
решение, столбец![]() является решением. А т.к. решение должно
быть единственным (определитель
является решением. А т.к. решение должно
быть единственным (определитель![]() ),
),![]() ;M(x)
находится аналогично Лемме
1 ; теорема
доказана.
;M(x)
находится аналогично Лемме
1 ; теорема
доказана.
Обобщая все вышесказанное, получаем: («Теорему о разложении на простейшие дроби»)
Пусть
многочлен
![]() представим в виде:
представим в виде:![]() и положим
и положим![]() ,
тогда
,
тогда
![]()

Заметим, что в самой последней дроби степень числителя (первая) меньше степени знаменателя (вторая) , т.е. последняя дробь – правильная. И каждую из дробей-слагаемых мы можем проинтегрировать в элементарных функциях.
Общий вывод: Любая рациональная дробь интегрируется в элементарных функциях.
Билет 32
