Производная сложной функции.

Теорема:

Пусть функция такая, что , и функция такая, что , . Тогда функция и .

Доказательство:

дифференцируема в точке , тогда:

Рассмотрим ∆H:

Билет 6

Производные элементарных функций.

1. ;

2.

3.

4.

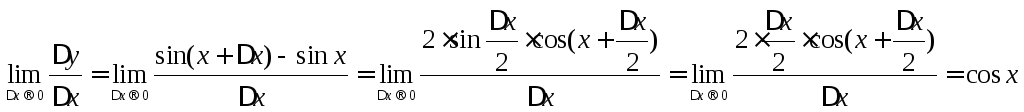(т.к. функция непрерывна)

Замечание: если функция имеет конечную производную в точке, то она непрерывна в этой точке (было доказано в Билете 1), но она может быть разрывной в любой другой точке, кроме этой.

Пример:

, т.к.

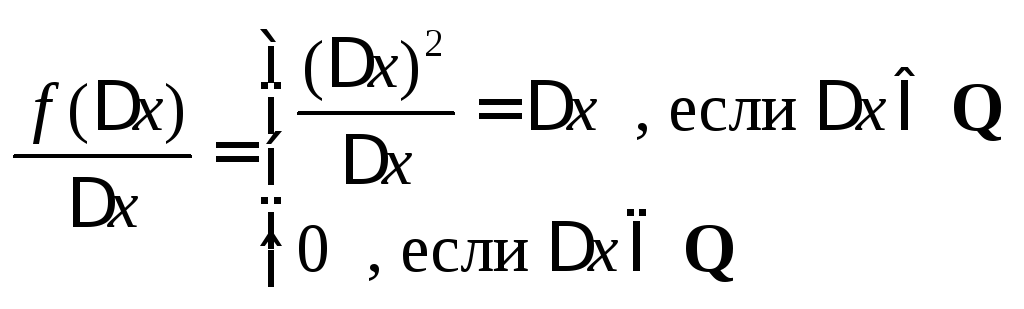
- не выполняется критерий Коши и в каждой точке функция разрывна.

Билет 7 Дифференциал функции. Определение. Геометрический смысл.

Если функция f имеет производную f΄(x_o) в точке x_o, то существует предел , где Δf=f(x_o+Δx)-f(x_o),,или, гдеA=f΄(x_o).

Определение:

Функция f дифференциируема в точке x_o, если ее приращение представимо в виде:

, где AΔx=df. (*)

Дифференциал — это главная линейная часть приращения функции.

Если существует конечная производная f΄(x_o) в точке x_o, то функция f(x) дифференцируема в этой точке.

Верно и обратное: если функцияf дифференцируема в точке x_o, т.е. ее приращение представимо в виде (*), то она имеет производную в точке x_o, равную A:

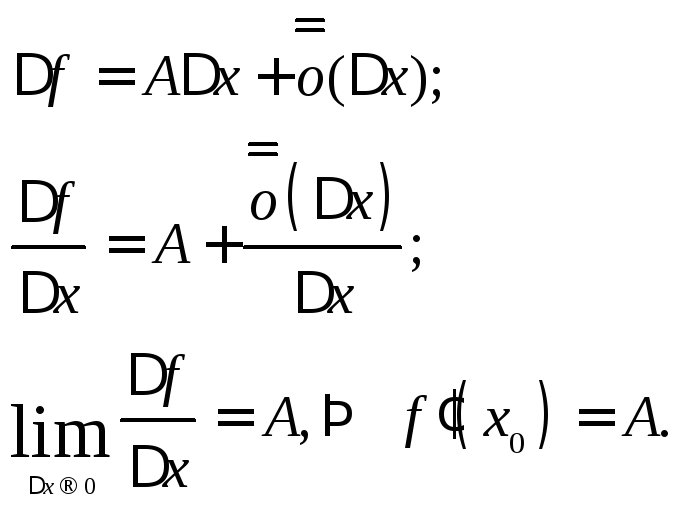
Геометрический смысл дифференциала:

A и B – точки графика f(x), соответствующие значениям x_o и (x_o+Δx) независимой переменной. Ординаты точек A и B соответственно равны f(x_o) и f(x_o+Δx). Приращение функции Δf=f(x_o+Δx)-f(x_o) в точке x_o равно длине отрезка BD и представимо в виде суммы Δf=BD=DC+CB, где DC=tgαΔx=f΄(x_o)Δx и α есть угол между касательной в точке A к графику и положительным направлением оси x. Отсюда видно, что DC есть дифференциал функции f в точке x_o:

DC=df=f΄(x_o)Δx.

При этом на долю второго члена CB приращения Δf приходится величина . Эта величина, при больших Δx, может быть даже больше, чем главный член, но она есть бесконечно малая более высокого порядка, чем Δx, когда Δx→0.

Билет 8

Необходимое и достаточное условие дифференцируемости.

Пусть функция имеет производную в точке(конечную): .

Тогда для достаточно малыхможно записать в виде суммыи некоторой функции, которую мы обозначим через, которая стремится к нулю вместе с:,

и приращение в точке может быть записано в виде:

или (1) ,

ведь выражение понимается как функция оттакая, что ее отношение кстремится к нулю вместе с.Пояснение:

Определение.

Функция называется дифференцируемой в точке, если ее приращение можно представить в виде:(2),

где А не зависит от , но вообще зависит от.

Теорема 1: Для того, чтобы функция была дифференцируемой в точке, необходимо и достаточно , чтобы она имела конечную производную в этой точке.

Доказательство:

Достаточность условия доказана выше: из существования конечной производной следовала возможность представленияв виде (1), где можно положить.

Необходимость условия. Пусть функция дифференцируема в точке. Тогда из (2), предполагая, получаем.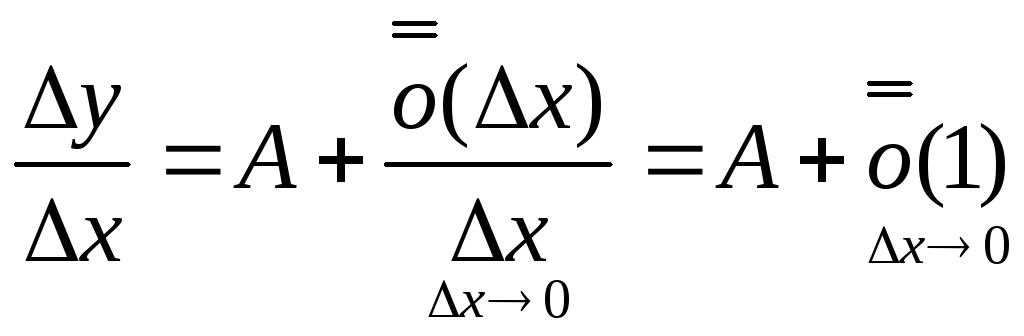

Предел правой части при существует и равен А:.

Это означает, что существует производная . Теорема доказана.

Билет 9