
обработка результатов измерений
.pdfГрафики строят на миллиметровой бумаге. Допускается построение графиков на тетрадном листе в клеточку. Размер графика – не менее чем 10×12 см. Графики строят в прямоугольной
системе координат, где по горизонтальной оси (оси абсцисс) откладывают аргумент, независимую физическую величину, а по вертикальной оси (оси ординат) – функцию, зависимую физическую величину.
Обычно график строят на основании таблицы экспериментальных данных, откуда легко установить интервалы, в которых изменяются аргумент и функция. Их наименьшее и наибольшее значения задают значения масштабов, откладываемых вдоль осей. Не следует стремиться поместить на осях точку (0,0), используемую как начало отсчета на математических графиках. Для экспериментальных графиков масштабы по обеим осям выбирают независимо друг от друга и, как правило, соотносят с погрешностью измерения аргумента и функции: желательно, чтобы цена наименьшего деления каждой шкалы примерно равнялась соответствующей погрешности.
Масштабная шкала должна легко читаться, а для этого необходимо выбрать удобную для восприятия цену деления шкалы: одной клетке должно соответствовать кратное 10 количество единиц откладываемой физической величины: 10n, 2 10n или 5 10n , где n – любое целое число, положительное или отрицательное. Так, числа 2; 0,5; 100; 0,02 – подходят, а числа 3; 7; 0,15 – не подходят для этой цели.
При необходимости масштаб по одной и той же оси для положительных и отрицательных значений откладываемой величины может быть выбран разным, но только в том случае, если эти значения отличаются не менее чем на порядок, т.е. в 10 раз и более. Примером может служить вольтамперная характеристика диода, когда прямой и обратный токи отличаются не менее, чем в тысячу раз: прямой ток составляет миллиамперы, обратный – микроамперы.
Стрелки, задающие положительное направление, на координатных осях обычно не указывают, если выбрано принятое положительное направление осей: снизу – вверх и слева – направо. Оси подписывают: ось абсцисс – справа внизу, ось ординат – слева вверху. Против каждой оси указывают название или символ откладываемой по оси величины, а через запятую – единицы ее измерения, причем все единицы измерения приводят в русском написании в системе СИ. Числовой масштаб выбирают в виде равноотстоящих по значению «круглых чисел», например: 2; 4; 6; 8 … или 1,82; 1,84; 1,86 …. Масштабные риски проставляют по осям на одинаковом расстоянии друг от друга, чтобы они выходили на поле графика. По оси абсцисс цифры числового масштаба пишут под рисками, по оси ординат – слева от рисок. Координаты экспериментальных точек возле осей проставлять не принято.
Экспериментальные точки аккуратно наносят на поле графика карандашом. Их всегда проставляют так, чтобы они были отчетливо различимы. Если в одних осях строят различные зависимости, полученные, например, при измененных условиях эксперимента или на разных этапах работы, то точки таких зависимостей должны отличаться друг от друга. Их следует отмечать разными значками (квадратами, кружками, крестиками и т.п.) или наносить карандашами разного цвета.
Расчетные точки, полученные путем вычислений, размещают на поле графика равномерно. В отличие от экспериментальных точек, они должны слиться с теоретической кривой после ее построения. Расчетные точки, как и экспериментальные, наносят карандашом – при ошибке неверно поставленную точку легче стереть.
На рисунке 5 приведена полученная по точкам экспериментальная зависимость, которая построена на бумаге, имеющей координатную сетку.
Через экспериментальные точки с помощью карандаша проводят плавную кривую, так чтобы точки в среднем были одинаково расположены по обе стороны от проведенной кривой. Если известно математическое описание наблюдаемой зависимости, то теоретическая кривая проводится точно так же. Нет смысла стремиться провести кривую через каждую экспериментальную точку – ведь кривая является только интерпретацией результатов измерений, известных из эксперимента с погрешностью. По сути, есть только экспериментальные точки, а кривая – произвольное, не обязательно верное, домысливание
10

эксперимента. Представим, что все экспериментальные точки соединены и на графике получилась ломаная линия. Она не имеет ничего общего с истинной физической зависимостью! Это следует из того, что форма полученной линии не будет воспроизводиться при повторных сериях измерений.
Рисунок 5 – Зависимость коэффициента динамической вязкости воды от температуры
Напротив, теоретическую зависимость строят на графике таким образом, чтобы она плавно проходила по всем расчетным точкам. Это требование очевидно, так как теоретические значения координат точек могут быть вычислены сколь угодно точно.
Правильно построенная кривая должна заполнять все поле графика, что будет свидетельством правильного выбора масштабов по каждой из осей. Если же значительная часть поля оказывается незаполненной, то необходимо заново выбрать масштабы и перестроить зависимость.
Результаты измерений, на основании которых строят экспериментальные зависимости, содержат погрешности. Чтобы указать их значения на графике, используют два основных способа.
Первый упоминался при обсуждении вопроса выбора масштабов. Он состоит в выборе цены деления масштабной шкалы графика, которая должна равняться погрешности откладываемой по данной оси величины. В таком случае точность измерений не требует дополнительных пояснений.
Если достичь соответствия погрешности и цены деления не удается, используют второй способ, заключающийся в прямом отображении погрешностей на поле графика. А именно, вокруг проставленной экспериментальной точки строят два отрезка, параллельные осям абсцисс и ординат. В выбранном масштабе длина каждого отрезка должна равняться удвоенной погрешности величины, откладываемой по параллельной оси. Центр отрезка должен приходиться на экспериментальную точку. Вокруг точки образуются как бы ”усы”, задающие область возможных значений измеряемой величины. Погрешности становятся зримыми, хотя “усы” могут невольно засорить поле графика. Отметим, что указанный способ чаще всего применяют тогда, когда погрешности меняются от измерения к измерению. Иллюстрацией способа служит рисунок 6.
6. Оценка параметров линейной зависимости
Обработка экспериментально полученной зависимости состоит в проведении по зарегистрированным точкам теоретической кривой, рассчитанной для заданного набора численных значений параметров. Варьируя параметры, добиваются наилучшего совпадения теоретической кривой с экспериментальными данными. Достижению такого совпадения помогает обязательное требование: теоретическая кривая должна отражать все особенности поведения экспериментальной зависимости, а, тем более, не давать повода для сомнений в совпадении с ней.
11
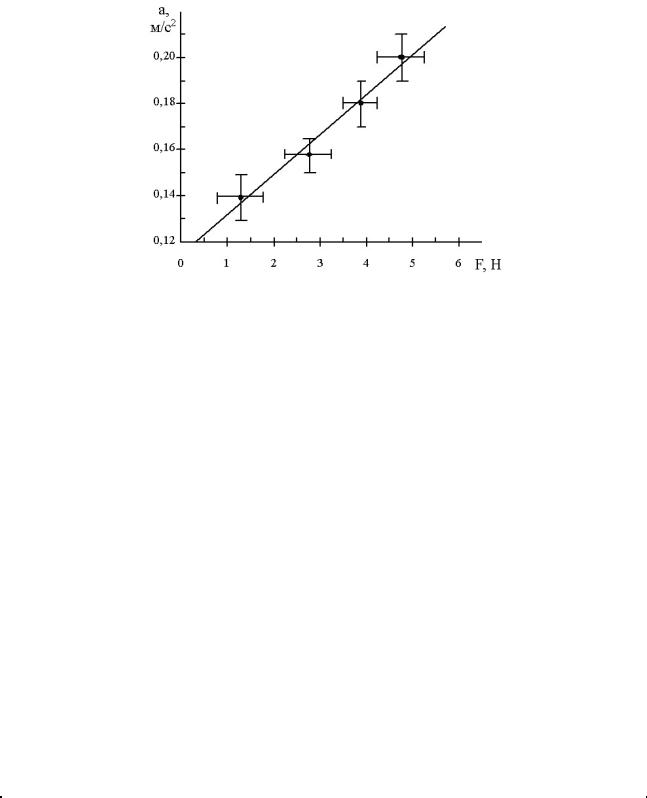
Рисунок 6 – Зависимость ускорения тела от силы, приложенной к нему
В эксперименте часто проверяют линейную зависимость двух величин вида
y = k x+ b, (29)
где x, y – измеряемые величины, k, b – параметры зависимости. Даже если из модельного описания непосредственно не получается линейная зависимость величин, теоретическую зависимость стремятся преобразовать к линейной. Объясняется это тем, что линейная зависимость выделена по отношению к другим формам функциональной связи двух величин. Во-первых, в силу психологических причин восприятие человека обладает свойством распознавать прямые линии, как встречающиеся в повседневной жизни, так и построенные в виде графиков. Визуально удается достаточно точно восстановить из графика всю прямую, даже в той области, где информация о ней частично отсутствует. Это означает, что проводимая “на глаз” прямая, которая проходит по точкам, содержащим экспериментальный разброс, оказывается удивительно близкой к оптимальной, построенной с помощью методов математической статистики. Собственно, возможности статистики применительно к линейной зависимости определяют второе обстоятельство ее частого использования. Дело в том, что параметры линейной зависимости и их погрешности могут быть надежно оценены на основе метода, называемого методом наименьших квадратов. Ниже, помимо этого метода, рассмотрены варианты графической и простой статистической (метод парных точек) обработки линейной зависимости.
6.1. Линеаризация зависимостей
В силу указанных выше причин экспериментатор должен стремиться свести нелинейную зависимость двух величин друг от друга к линейной, а затем обработать ее наилучшим образом. Как правило, многие функционально сложные зависимости допускают преобразование координат, приводящее к искомому результату. Примеры подобных преобразований помещены в таблице 2.
Таблица 2 – Примеры линеаризации зависимостей.
Вид |
нелинейной |
Получаемая линейная |
y |
x |
k |
b |
|
зависимости |
зависимость |
||||||
|
|
|
|
||||
|
v=a uz |
ln v=z ln u + ln a |
ln v |
ln u |
z |
ln a |
|
|
v=a ezu |
ln v=z u + ln a |
ln v |
u |
z |
ln a |
|
|
v= a ez/u |
ln v=z u-1 + ln a |
ln v |
u-1 |
z |
ln a |
|
|
v=u/(a+z u) |
v-1=a u-1 + z |
v-1 |
u-1 |
k |
z |
|
|
|
12 |
|
|
|
|
|

В ней использованы следующие обозначения: v, u – преобразуемые функция и ее аргумент, y, x – новые функция и аргумент (после преобразования). По завершении обработки данных, то есть после определения средних значений и погрешностей параметров преобразованной зависимости, полученные результаты используют для пересчета к первоначальным параметрам. Пересчет выполняют по правилам, используемым для обработки результатов косвенных измерений.
6.2. Определение параметров линейной зависимости из графика
После нанесения на график экспериментальных точек по ним «на глаз» проводят прямую. Строят ее таким образом, чтобы точки в среднем одинаково располагались по обе стороны от прямой. На рисунке 7 это прямая 1-2. На ней выбирают две точки максимально удаленные друг от друга.
Рисунок 7 – Графическая обработка линейной зависимости.
Их координаты x1, y1 и x2, y2 подставляют в (29) для получения двух уравнений с неизвестными k и b
y1=k x1+b,
y2=k x2+b,
из которых находят
k = |
y1 |
− y2 |
, |
b = |
y2 x1 − y1 |
x 2 |
. |
(30) |
x1 |
−x 2 |
x1 −x 2 |
|
|||||
|
|
|
|
|
|
Для оценки погрешностей σ(k) и σ(b) строят две дополнительные прямые, симметричные относительно прямой 1-2, чтобы экспериментальные точки, в основном, располагались между ними. Если на графике имеются точки, которые отстоят от основной прямой 1-2 более чем на утроенное среднее расстояние точек до прямой (это хорошо заметно уже при рассматривании графика – такой точкой является точка А), то их отбрасывают и не используют при построении дополнительных прямых. Соответствующие измерения, скорее всего, содержат промахи. Дополнительные прямые определяют «коридор погрешностей» эксперимента, внутри которого находится исследуемая линейная зависимость. Предельные случаи хода этой зависимости получатся, если провести прямые через противоположные углы «коридора» (прямые 4-5 и 3-6). Тем же способом, что и для основной прямой 1-2, находят параметры предельных прямых k1, b1 и k2, b2 . Оценки погрешностей
σ(k)= |
|
k1 − k 2 |
|
|
, |
σ(b)= |
|
|
b1 − b2 |
|
|
. |
(31) |
|
|
|
|
||||||||||
|
|
|
|
||||||||||
2 |
|
|
2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|||||
Может оказаться, что теоретическую зависимость между измеряемыми величинами предполагают линейной, а экспериментальные точки явно не ложатся на прямую. Проведение по ним прямой неправомерно. Расхождение между теоретической и экспериментальной зависимостями свидетельствует о наличии систематических
13
погрешностей, которые должны быть выявлены и учтены при обработке результатов. Иначе экспериментатору остается только констатировать расхождение модели с экспериментом. Часто линейная зависимость является приближенно справедливой в ограниченном интервале изменения физических величин. В таком случае необходимо определить границы применимости линейной зависимости и указать их при анализе результатов эксперимента.
6.3. Метод парных точек
В некоторых физических экспериментах основной интерес представляет только угловой коэффициент (параметр k) зависимости (29). Для оценки значения коэффициента и определения его погрешности удобен метод парных точек. Он заключается в следующем.
После нанесения на график экспериментальных точек из них выбирают пары, в которых точки отстоят друг от друга примерно на одинаковое расстояние. Желательно, чтобы это расстояние было максимально возможным. Через каждую пару проводят прямую, а затем согласно (30) вычисляют угловые коэффициенты всех прямых. Из получившегося набора коэффициентов по правилам обработки данных прямых измерений определяют среднее значение коэффициента и его погрешность. Их принимают за результат измерения искомого параметра зависимости (29).
Следует отметить, что аналогичным образом в зависимости (29) можно найти свободный член (параметр b). По парам точек согласно (30) вычисляют свободные члены всех полученных прямых. Затем указанным выше способом рассчитывают среднее значение и погрешность.
Рассмотрим пример конкретной обработки данных эксперимента по измерению массы m тела, движущегося под действием силы F с ускорением a. Измеренные значения ускорения a и соответствующие им значения силы F приведены в таблице 3.
Таблица 3 – Зависимость ускорения тела от приложенной силы.
№ п/п |
a, м/с2, 10-3 |
F, мН |
1 |
13,2 |
11,07 |
2 |
16,9 |
19,09 |
3 |
25,3 |
28,94 |
4 |
44,3 |
36,03 |
5 |
46,1 |
46,88 |
6 |
62,7 |
57,31 |
7 |
70,0 |
67,59 |
8 |
81,1 |
76,91 |
Теоретическое описание исследуемой зависимости дает второй закон Ньютона a=F/m, где величина 1/m является угловым коэффициентом линейной зависимости, проходящей через начало координат. Значит, для его определения можно воспользоваться методом парных точек. Нанесем экспериментальные точки на график (рисунок 8) и пронумеруем их по порядку от 1 до 8. Выберем пары точек 1-5, 2-6, 3-7, 4-8 и занесем их координаты в таблицу 4, которую используем для проведения необходимых вычислений.
Таблица 4 – Обработка данных методом парных точек.
Пары точек |
ai, м/с2 |
Fi, |
mi |
= |
Fi |
|
, кг |
mi–mср, |
(mi–mср)2 |
||||
10 |
-3 |
мН |
a i |
кг |
10 |
-3 |
кг |
2 |
|||||
|
|
|
|
|
|
|
|||||||
1-5 |
32,9 |
35,81 |
|
1,0884 |
|
0,11379 |
12,948 |
||||||
2-6 |
45,8 |
38,22 |
|
0,83450 |
-0,14011 |
19,631 |
|||||||
3-7 |
44,7 |
38,65 |
|
0,86465 |
-0,10996 |
12,091 |
|||||||
4-8 |
36,8 |
40,88 |
|
1,1109 |
|
0,13629 |
18,575 |
||||||
14
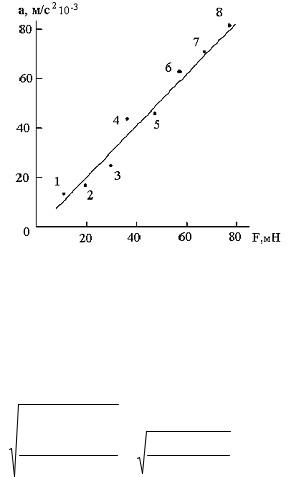
Рисунок 8 – Зависимость ускорения тела от приложенной силы.
Для каждой i-й пары точек по угловому коэффициенту наклона прямой, проведенной через эти точки определяется масса тела mi, а, затем, находится величина массы и ее среднеквадратичное отклонение:
mср≈0,97461 кг, ∑n (mi −mср )2 ≈63,245 10-3 кг2,
|
i=1 |
|
|
|
|
|
|
∑n (mi − mср )2 |
|
63,245 10 |
−3 |
||
Sm = |
i=1 |
= |
=0,072598 кг. |
|||
4 |
3 |
|||||
|
n(n −1) |
|
|
|||
Для n=4 и доверительной вероятности P=0,95 коэффициент Стьюдента t(0,95; 4)=3,2 (см.
таблицу 1). Погрешность σ(m)=0,072598 3,2≈ 0,23231 кг.
Окончательный результат m=(0,97±0,23) кг.
Точность измерения массы невелика, что свидетельствует о наличии значительных экспериментальных погрешностей.
6.4. Метод наименьших квадратов
Пусть в результате эксперимента мы получили ряд измерений величины y: y1, y2, …, yn, соответствующих значениям аргумента x: x1, x2, …, xn, которые могут быть представлены на графике (рисунок 9) в виде точек (y1, x1), (y2, x2),…, (yn, xn). Необходимо установить эмпирическую зависимость между y и x (аппроксимировать экспериментальную зависимость прямой линией).
Если соединить полученные точки ломаной линией, то очевидно, что она не будет описывать искомую зависимость, так как изменится при повторных измерениях. Задача заключается в нахождении такой функции y=f(x), которая как можно ближе подходила к истинной зависимости. Теория вероятности показывает, что наилучшим приближением будет такая кривая (или прямая) линия, для которой сумма квадратов расстояний по вертикали от точек до кривой будет минимальной (рисунок 9)
n
∑
i=1
|
n |
)2 = {min}. |
|
yi2 |
= ∑(yi − y′i |
(32) |
i=1
Целью метода наименьших квадратов является нахождение такой функциональной зависимости, которая бы удовлетворяла условию (32).
Большинство зависимостей может быть представлено теоретически в виде полинома m-й степени
y = a 0 + a1 x + a 2 x 2 +... + a m x m . |
(33) |
15 |
|

Рисунок 9 –Зависимость y=f(x).
Задача заключается в определении коэффициентов a0, a1, … am искомой зависимости. Рассмотрим простейший, но часто встречающийся на практике случай линейной зависимости
y=k x+b.
Значения параметров k и b требуется определить так, чтобы точки располагались как можно ближе к искомой прямой. Если разброс точек относительно прямой подчиняется закону нормального распределения, то мерой этого разброса является среднеквадратичное отклонение.
Уравнение прямой можно выразить через экспериментальные значения xi
yi′=k xi+b.
Тогда условие (32) можно записать в виде
n
∑
i=1
|
n |
|
yi2 |
= ∑(yi −k x i −b)2 = {min}. |
(34) |
i=1
Требуется найти, при каких k и b будет выполняться (34). Определим минимум функции (34), то есть найдем частные производные по параметрам k и b и приравняем их к нулю
−
−
n |
|
|
2∑(yi −k x i −b) x i = 0, |
|
|
i=1 |
(35) |
|
n |
||
|
||
2∑(yi −k x i −b)= 0. |
|
|
i=1 |
|
Решая систему уравнений (35) относительно параметров прямой k и b, придем к следующим соотношениям
|
|
|
|
n |
[(x i −x) yi ] |
|||||
|
|
|
|
∑ |
||||||
|
|
k = |
i=1 |
|
|
|
|
|
, |
|
|
|
|
|
|
D |
|
|
|||
|
|
|
n |
|
|
|
n |
|||
|
|
1 |
|
|
|
1 |
||||
где |
x = |
∑x i , |
|
y = |
∑yi , |
|||||
n |
|
n |
||||||||
|
|
i=1 |
|
|
|
i=1 |
||||
Оценка погрешности параметров k и b |
|
|
||||||||
|
|
|
n |
|
|
|
|
|
|
|
|
σ(k)= |
|
∑ yi |
2 |
|
|
σ(b)= |
|||
|
|
i=1 |
|
|
, |
|
||||
|
|
|
(n − 2) D |
|
|
|
|
|||
|
b = y −k x, |
|
|
(36) |
|||||||||
|
|
|
1 |
|
|
n |
|
|
|
|
|
|
|
D = |
|
∑(x i −x)2 . |
|
|
(37) |
||||||||
n |
|
|
|||||||||||
|
|
|
i=1 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
1 |
|
|
|
x |
2 |
|
∑ yi |
2 |
|
|
||
|
|
+ |
|
|
|
|
|
i=1 |
|
, |
(38) |
||
|
|
|
|
||||||||||
n |
|
D |
|
|
(n − 2) |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где yi=yi–y= yi–k xi–b – отклонение экспериментального значения yi от значения, полученного по теоретической кривой (рисунок 9).
Если заранее известно, что физическая зависимость имеет вид прямой, исходящей из начала координат, т.е. коэффициент b=0 в уравнении прямой, то коэффициент k будет определяться только первым уравнением системы (35) при b=0. Коэффициент k в этом случае
16
|
n |
|
|
||
|
∑[x i yi ] |
|
|
||
k = |
i=1 |
|
. |
(39) |
|
n |
|||||
|
|
|
|||
|
∑x i2 |
|
|
||
i=1
Вкачестве иллюстрации метода рассмотрим пример конкретной обработки данных из предыдущего пункта по изучению зависимости силы от ускорения (таблица 3). Требуется определить зависимость (аппроксимировать) ускорения от результирующей силы F. В этом случае II закон Ньютона устанавливает прямую пропорциональность между ускорением и
результирующей силой a=k F, где в качестве коэффициента пропорциональности выступает величина обратная массе тела k=1/m. Таким образом, указанная зависимость a=f(F) имеет вид прямой исходящей из начала координат.
Результаты расчетов по формулам (37-39) приведены в таблице 5. При расчете n=8, в качестве величины yi выступает ai, в качестве величины xi – величина Fi.
Таблица 5 – Результаты расчетов по методу наименьших квадратов
8 |
[a |
|
F ] |
8 |
k |
m=1/k |
|
∑ |
i |
F2 |
|
|
|||
|
|
i |
∑ i |
|
|
||
i=1 |
|
|
|
|
i=1 |
|
|
19,520 10-3 |
18,588 10-3 |
1,0501 |
0,95226 |
||||
|
|
|
|
|
D |
σ(k) |
σ(m) |
|
|
F |
|
||||
42,978 10-3 |
476,48 10-6 |
0,18447 |
0,16728 |
||||
Используя формулу (19) для расчета погрешности косвенного измерения величины m=1/k, можно определить ее погрешность σ(m)=σ(k)/k2.
После округления результатов получим: k=1,05±0,18 кг-1; m=0,95±0,17 кг-1.
Сравнивая результат с результатами расчета в предыдущем пункте, приходим к выводу, что величина массы и ее погрешность имеют приблизительно одинаковые значения, оцененные двумя различными методами. Доверительные интервалы оценок пересекаются.
Аппроксимирующая прямая
a=1,05 F.
7. Правила оформления отчета по лабораторной работе
Отчет по лабораторной работе оформляется на скрепленных листах формата А4, либо используется тетрадь в клеточку (в сответствии c [13, 14]). После титульного листа в заголовке указывается номер лабораторной работы и ее название. Далее следуют пункты.
7.1.Введение
7.2.Описание установки и методики измерения
Здесь необходимо кратко отразить методику эксперимента; зарисовать схему установки, иллюстрирующую принцип действия, физическое явление; отобразить графики, характеризующие природное явление. Все иллюстрации должны быть пронумерованы и иметь названия.
7.3. Основные расчетные формулы Необходимо привести расчетные формулы и их вывод. В том числе и формулы для оценки погрешностей.
7.4. Результаты работы и их анализ Экспериментальную часть начинают таблицы с экспериментальными и исходными
данными. Далее идут расчеты, экспериментальные графики. Таблицы и графики должны быть пронумерованы, и иметь названия. Расчеты должны быть приведены все, включая обработку результатов измерения. Записывается искомая величина, после знака "равно" – формула, по которой величина определяется. После знака "равно" необходимо привести
17
числа, подставляемые в формулу. Далее, ответ и единица измерения. Обработка
результатов измерений проводится во всех лабораторных работах.
7.5. Заключение В заключении формулируются выводы. Выводы формулируются исходя из
экспериментальных данных – как найденные величины зависят друг от друга? соответствует ли это теории? По виду и характеру графических зависимостей также формулируются выводы. Полученные зависимости и физические величины необходимо сравнить с теоретическими. Оценить расхождение. Окончательный вывод формулируется исходя из цели лабораторной работы.
При подготовке к защите лабораторных работ следует пользоваться как настоящим методическим пособием, так и литературой указанной в конце пособия, а также литературой, рекомендуемой преподавателем.
18

II. МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ЛАБОРАТОРНЫМ РАБОТАМ
1. Лабораторная работа 1. Измерение объема тела простой конфигурации
Введение
Основой любого эксперимента является измерение. Результаты любого физического эксперимента необходимо уметь анализировать. Это значит, что в физическом практикуме необходимо научиться не только измерять величины, но и находить связь между ними, сопоставлять результаты эксперимента с выводами теории.
Целью данной работы является получение навыков обработки результатов измерений и измерение объема тела в виде прямоугольного параллелепипеда.
1.1. Методика измерений
Принадлежности: деревянный брусок, штангенциркуль.
Преподавателем выдается тело, объем которого необходимо измерить, и прибор, измеряющий геометрические размеры (штангенциркуль). Правила пользования прибором
объясняются преподавателем на занятии. |
|
Объем параллелепипеда определяется косвенным методом по формуле |
|
Vп=a b c, |
(40) |
где a, b, c – длины граней параллелепипеда.
Измеряются длины граней a, b, c. Каждая длина измеряется несколько раз (от 3 до 9 раз) в разных местах поверхности, ограничивающей указанный размер.
1.2. Порядок проведения измерений
1.2.1.Получить принадлежности у преподавателя.
1.2.2.Определить систематическую погрешность прибора σсист, которая указана на шкале прибора. Количество измерений n указывается преподавателем. По количеству измерений и
доверительной вероятности выбрать коэффициент Стьюдента tn,P (таблица 1). Указанные данные записать в таблицу 6.
Таблица 6 – Исходные данные.
n |
P |
tn,P |
σсист, мм |
8 |
|
|
|
1.2.3. Провести измерения параметров (ai, bi, ci) n=8 раз. Результаты измерений записать в таблицу 7.
Таблица 7 – Измеренные значения длин граней параллелепипеда.
№ измерения, i |
ai, мм |
bi, мм |
ci, мм |
1 |
|
|
|
2 |
|
|
|
… |
|
|
|
1.2.4. Сдать принадлежности преподавателю. 1.3. Обработка результатов измерений
1.3.1.Обработку результатов прямых многократных измерений линейных размеров a, b, c провести согласно п. 3.2 (I) , где в качестве параметра Xi выступают значения ai или bi, ci.
1.3.2.Записать результаты расчетов в таблицу 8.
1.3.3.Результаты измеренных параметров записать в стандартном виде (15), указав доверительный интервал, и предварительно округлить. Результаты измерений следует записать в системе СИ.
19
