Пример 1.
Вычислить двойной интеграл
,
если область D задана
условиями
,
.
Решение.
Прежде всего, нужно
построить область D,
чтобы выяснить, является ли она правильной,
и если да, то в каком направлении.
Неравенство
определяет на плоскости вертикальную
полосу между прямыми
и
.
Неравенству
соответствует множество точек плоскости,
расположенных в горизонтальной полосе
между прямыми
и
.
Следовательно, область D
есть прямоугольник, изображенный на
рисунке 4. 
Легко убедиться, что эта
область правильная и в направлении оси
Ох, и в направлении оси Оу: все
прямые, проведенные через область
параллельно и в направлении оси Ох,
имеют одну линию «входа»
и одну линию «выхода»
.
Аналогично, все прямые, проведенные
через область параллельно (в направлении)
оси Оу, имеют одну линию «входа»
и одну линию «выхода»
.
Значит, для записи данного двойного
интеграла через повторные можно выбрать
любой порядок интегрирования.
Рассмотрим порядок
интегрирования «no
dx
- no
dy».
Он соответствует области, правильной
в направлении оси Оу.
Внешний интеграл берется по переменной
х, пределы интегрирования – проекция
области D на ось Ох,
это отрезок
.
Внутренний интеграл берется по переменной
у, пределы интегрирования –
соответственно «линия входа»
и «линия выхода»
в направлении оси Оу. Тогда имеем
Вычислим заданный двойной
интеграл, записав его через повторные,
используя порядок интегрирования «no
dy
- no
dx»,
и сравним результаты. В этом случае
рассматривается правильная
в направлении оси Ох
область. Внешний интеграл по у
берется по отрезку
– проекции области на ось Оу. Границы
внутреннего интеграла по х определяют
соответственно «линия входа»
и «линия выхода»
в направлении оси Ох. Тогда получим:
Как видим, получился тот же результат.
Пример 2.
Вычислить двойной интеграл
,
если область D
ограничена указанными линиями:
.
Решение.
Построим область D,
и определим, является ли она правильной,
и в каком направлении. 
Очевидно, заданная область
выглядит
так, как показано на рисунке 5. И эта
область является правильной как в
направлении оси Оу, так и в направлении
оси Ох. Значит, можно выбрать любой
порядок интегрирования.
Будем, например, интегрировать «no dx - no dy», т.е. рассматривать область D как правильную в направлении оси Оу. Тогда выполним действия, указанные в пункте 2 сформулированного выше правила (страница 5).
а) Найдем проекцию данной области на ось Ох. Для этого достаточно определить абсциссы крайних, «угловых», точек области, т.е. точек пересечения заданных линий:
.
Значит, проекцией области D на ось Ох является отрезок [0, 1].
б) Проведя
через любую точку области прямую,
параллельную оси Оу, видим, что если
двигаться вдоль этой прямой в направлении
оси Оу сквозь область, то линией
«входа» будет парабола
,
а линией «выхода» – прямая
.
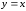в) Уравнения линий «входа» и «выхода» уже записаны в нужном виде – переменная у выражена через х.
г) Теперь запишем двойной
интеграл через повторные в соответствии
с полученными результатами. Внешний
интеграл будет вычисляться по х по
отрезку [0, 1]. Внутренний интеграл будем
вычислять по у, нижний предел
интегрирования будет равен
(правая
часть уравнения линии входа),
а верхний – равен х (правая
часть уравнения линии выхода). Тогда
получим:
=
.