
FAIT1 / Интегралы-Помощь / Двойной и криволинейные интегралы / Криволинейный первого рода
.docxКриволинейный интеграл первого рода
Пусть
на дуге
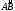 гладкой кривой L
определена непрерывная функция
гладкой кривой L
определена непрерывная функция
 .
Разобьем дугу
.
Разобьем дугу
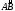 произвольным образом точками
произвольным образом точками
 на п частей. Длину частичной дуги
на п частей. Длину частичной дуги
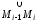 обозначим
обозначим
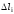 ,
а
,
а
 .
На каждой дуге
.
На каждой дуге
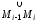 возьмем
произвольную точку Pi(i,
i)
и вычислим значения
возьмем
произвольную точку Pi(i,
i)
и вычислим значения
 .
Составим интегральную сумму
.
Составим интегральную сумму
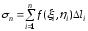 .
.
Определение
Если
существует конечный предел при n0
последовательности {n}
интегральных сумм, не зависящий ни от
способа разбиения дуги
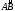 ,
ни от выбора точек Pi(i,
i),
то этот предел называется криволинейным
интегралом первого рода от функции
f(х, у) по дуге
,
ни от выбора точек Pi(i,
i),
то этот предел называется криволинейным
интегралом первого рода от функции
f(х, у) по дуге
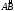 и обозначается
и обозначается
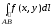 .
.
Таким образом, по определению
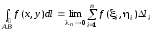 ,
,
Криволинейный
интеграл I
рода называют еще криволинейным
интегралом по длине
дуги (т.к.
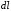 есть дифференциальный элемент длины
дуги кривой
есть дифференциальный элемент длины
дуги кривой
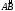 ).
).
Свойства криволинейного интеграла первого рода:
1.
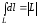 ,
где
,
где
 –
длина дуги
–
длина дуги
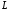 (геометрическая интерпретация
криволинейного интеграла I
рода).
(геометрическая интерпретация
криволинейного интеграла I
рода).
2.
Криволинейный интеграл I
рода не зависит от направления пути
интегрирования, т.е.
 .
.
3.
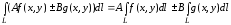 - свойство линейности
- свойство линейности
4.
Если
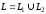 ,
то
,
то
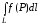 =
=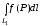 +
+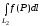 (свойство
аддитивности)
(свойство
аддитивности)
5.
Если f(P)
g(P),
то
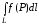
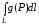
6.
Если m
f(P)
M, PL,
то mL
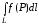
ML
ML
7.
Существует точка Q
L:
 =
f(Q)L
(Теорема о среднем.)
=
f(Q)L
(Теорема о среднем.)
С
физической точки
зрения
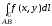 определяет массу материальной
кривой (массу тонкого
неоднородного криволинейного стержня)
с плотностью
определяет массу материальной
кривой (массу тонкого
неоднородного криволинейного стержня)
с плотностью
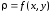 :
:
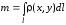 .
.
Статические
моменты относительно осей координат
материальной кривой l
с плотностью
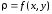 определяются
по формулам
определяются
по формулам
 ,
,
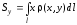 ,
,
а координаты центра масс такой кривой равны
 ,
,
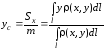 .
.
Кроме
того, для материальной кривой l
моменты инерции
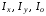 относительно
осей Ох, Оу и начала координат
равны соответственно
относительно
осей Ох, Оу и начала координат
равны соответственно
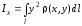 ,
,
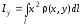 ,
,
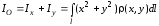 .
.
Вычисление криволинейного интеграла первого рода
Вычисление криволинейного интеграла I рода, также как и двойного интеграла, сводится к вычислению определенного интеграла.
-
Если кривая L задана уравнением y = (x), а дуга
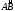 соответствует изменению x
на отрезке [a, b],
то
соответствует изменению x
на отрезке [a, b],
то
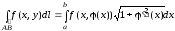
-
Если
 определена уравнением x
= (y),
y
[c, d],
то
определена уравнением x
= (y),
y
[c, d],
то
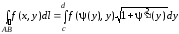 .
.
-
Если дугу
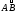 определяют параметрические уравнения
определяют параметрические уравнения
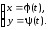 t[,],
то
t[,],
то
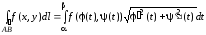 .
.
Рассмотрим примеры вычисления криволинейных интегралов I рода.
Пример 1.
Вычислить
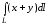 ,
если L:
,
если L:
а) отрезок прямой 3x–2y+6=0 между точками A(-2,0) и B(2,6);
б) верхняя половина
окружности
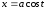 ,
,
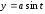 .
.
Решение.
а) Чтобы преобразовать заданный криволинейный интеграл к определенному интегралу, нужно линию L, по которой идет интегрирование, описать условиями одного из трех видов:
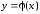 ,
где
,
где
 ;
;
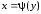 ,
где
,
где
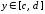 ;
;
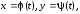 где
где
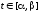 .
.
В нашей задаче
линия L
задана уравнением 3x–2y+6=0.
Выразим из этого уравнения переменную
у:
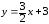 .
Поскольку рассматривается отрезок АВ
этой прямой, где A(-2,0)
и B(2,6),
то на этом отрезке переменная х
принимает значения из промежутка
.
Поскольку рассматривается отрезок АВ
этой прямой, где A(-2,0)
и B(2,6),
то на этом отрезке переменная х
принимает значения из промежутка
 .
Следовательно, линия L
определена условиями вида
.
Следовательно, линия L
определена условиями вида
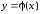 ,
,

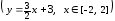 .
Поэтому преобразование криволинейного
интеграла к определенному интегралу
производим по формуле
.
Поэтому преобразование криволинейного
интеграла к определенному интегралу
производим по формуле
 .
.
Тогда имеем
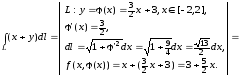

В этой задаче
переменной интегрирования можно было
выбрать также y,
выразив из уравнения прямой переменную
х
через у:
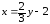 .
При этом на отрезке АВ переменная у
принимает значения из промежутка
.
При этом на отрезке АВ переменная у
принимает значения из промежутка
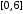 .
Тогда линия интегрирования L
будет определена условиями вида
.
Тогда линия интегрирования L
будет определена условиями вида
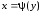 ,
,
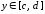 и переход к определенному интегралу
осуществляется по формуле:
и переход к определенному интегралу
осуществляется по формуле:
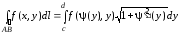 .
.
Используя эту формула, получим
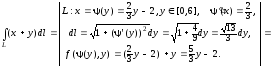
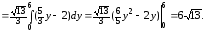
Получили тот же
результат.
б)
Параметрические
уравнения
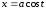 ,
,
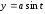 определяют на координатной плоскости
окружность с центром в начале координат
и радиусом a
(рис.1), причём верхняя половина этой
окружности соответствует изменению
параметра t
от 0 до π.
определяют на координатной плоскости
окружность с центром в начале координат
и радиусом a
(рис.1), причём верхняя половина этой
окружности соответствует изменению
параметра t
от 0 до π.
Рисунок 1
Поскольку линия
интегрирования L
задана условиями вида
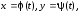
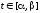 ,
то преобразование криволинейного
интеграла к определенному производим
по формуле:
,
то преобразование криволинейного
интеграла к определенному производим
по формуле:
 .
.
Тогда получим
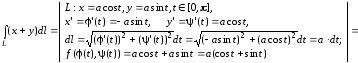
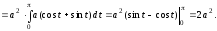
Пример 2.
Найти массу дуги параболы y2 = 2x + 4 между точками пересечения её с осями координат, если плотность масс в любой точке дуги пропорциональна ординате этой точки.
Решение.
Парабола
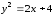 ,
или
,
или
 симметрична относительно оси Ох,
вершина её находится в точке
симметрична относительно оси Ох,
вершина её находится в точке
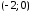 .
Ось Ох
эта
парабола пересекает в точке
.
Ось Ох
эта
парабола пересекает в точке
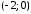 ,
а в точках
,
а в точках
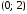 и
и
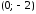 она пересекает ось Оу (рис. 2). Найдем
массу дуги l параболы,
заключенной между точками
она пересекает ось Оу (рис. 2). Найдем
массу дуги l параболы,
заключенной между точками
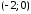 и
и
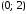 .
.
В
каждой точке этой дуги, по условию,
плотность масс пропорциональна ординате
этой точки, и значит, равна
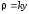 ,
где
,
где
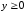 ,
а
,
а
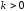 – коэффициент пропорциональности.
– коэффициент пропорциональности.
Как отмечалось выше (стр.2), масса материальной дуги кривой может быть найдена по формуле
 .
.
Значит, масса рассматриваемой дуги l параболы равна
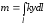 .
.
Чтобы
преобразовать этот криволинейный
интеграл к определенному, запишем
уравнение параболы в виде
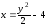 .
На рассматриваемой дуге параболы y
[0, 2]. Тогда
.
На рассматриваемой дуге параболы y
[0, 2]. Тогда
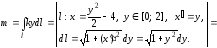

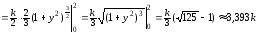 (ед.
массы).
(ед.
массы).
Аналогично
понятию криволинейного интеграла по
кривой на плоскости (в
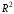 )
может быть дано понятие криволинейного
интеграла по пространственной кривой.
)
может быть дано понятие криволинейного
интеграла по пространственной кривой.
Пусть
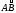 – дуга гладкой пространственной кривой,
на которой определена и непрерывна
функция
– дуга гладкой пространственной кривой,
на которой определена и непрерывна
функция
 .
Тогда
.
Тогда
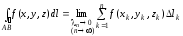 ,
,
где
 –
длины отрезков разбиения дуги
–
длины отрезков разбиения дуги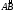 ,
,
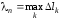 ,
(
,
(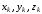 )
–произвольная точка, взятая на k-той
частичной дуге разбиения.
)
–произвольная точка, взятая на k-той
частичной дуге разбиения.
Если
дуга
 задана условиями:
задана условиями:
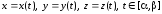 ,
то
,
то
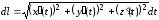 и
и
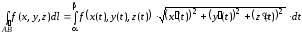 .
.
Пример 3.
Вычислить
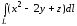 ,
если L
– отрезок прямой от точки A(1,0,1)
до точки B(0,3,4).
,
если L
– отрезок прямой от точки A(1,0,1)
до точки B(0,3,4).
Решение.
Чтобы вычислить данный интеграл, нужно сначала описать уравнениями линию, по которой идет интегрирование. Поскольку это – прямая, проходящая через заданные точки, то чтобы найти её уравнения, используем соответствующую формулу:
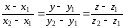 .
.
Получим:



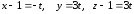

Из этих уравнений
координаты точки
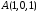 получаются при
получаются при
 ,
а координаты точки
,
а координаты точки
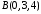 получаются
при
получаются
при
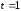 .
Таким образом, линия интегрирования L
определяется условиями
.
Таким образом, линия интегрирования L
определяется условиями
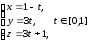 .
.
Тогда
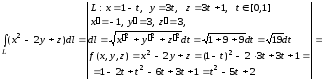
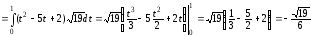 .
.
Пример 4.
Найти центр масс
контура треугольника с вершинами
 ,
,
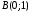 ,
,
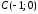 ,
если плотность в каждой точке этого
контура равна сумме квадратов координат
этой точки.
,
если плотность в каждой точке этого
контура равна сумме квадратов координат
этой точки.
Решение.
Чтобы найти координаты центра масс данной кривой, используем формулы, приведенные на странице 2:
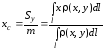 ,
,
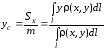 .
.
Найдем сначала
массу линии – контура треугольника
АВС.
По условию, плотность масс в каждой
точке кривой равна сумме квадратов
координат этой точки, значит,
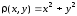 .
Контур рассмотренного треугольника
состоит из трех участков (рис.3): АВ,
ВС,
АС.
Найдем массу каждого участка отдельно:
.
Контур рассмотренного треугольника
состоит из трех участков (рис.3): АВ,
ВС,
АС.
Найдем массу каждого участка отдельно:
-
Участок АВ задается уравнением
 *),
*),
 .
Тогда
.
Тогда
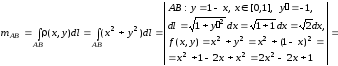
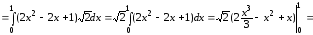
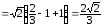 .
.
-
Участок ВC задается уравнением
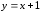 *),
*),
 .
Тогда
.
Тогда
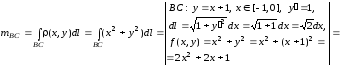
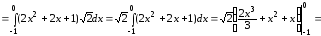
 .
.
-
Участок АC задается уравнением
 .
Тогда
.
Тогда
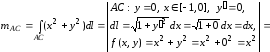
 .
.
Следовательно, масса всего контура треугольника равна
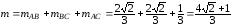 .
.
Найдем статические моменты контура относительно осей координат. Учитывая предыдущие вычисления, получим


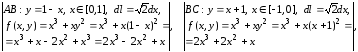



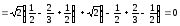 .
.
Аналогично
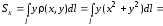

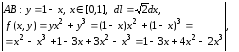
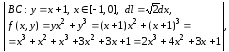
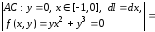

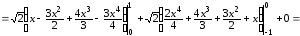
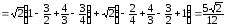 .
.
Тогда
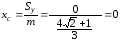 ,
,
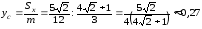 .
.
Таким образом,
центр масс контура заданного треугольника
АВС
находится в точке
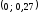 .
.
*)*) Уравнение этого участка можно найти как уравнение прямой, проходящей через точки (1,0) и (0, 1):
*)*) Это отрезок прямой, проходящей через точки (–1,0) и (0, 1), поэтому.
