
Криволинейный интеграл второго рода
Пусть в некоторой области D пространства R2 определены две непрерывные функции P(x,y), Q(x,y). Тогда в любой точке М(x,y)D может быть задана векторная функция двух скалярных аргументов

D векторной форме эта функция может быть записана так:
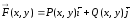 .
.
Пусть
функции P(x,
y) и Q(x,
y) определены во всех
точках гладкой дуги
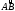 кривой LD.
Разобьем дугу
кривой LD.
Разобьем дугу
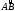 на части точками М1, М2,
... Мn. На
каждой дуге
на части точками М1, М2,
... Мn. На
каждой дуге
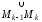 возьмем произвольную точку
возьмем произвольную точку
 и вычислим значение
и вычислим значение 
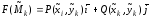 .
.
Пусть
отрезки [a, b]
и [c, d]
– проекции дуги
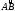 на оси Oх и Oу
соответственно, т.е. если точка М(х,
у)
на оси Oх и Oу
соответственно, т.е. если точка М(х,
у) ,
то x[a,b],
y[c,
d]. Каждую частичную
дугу спроектируем на оси координат,
получим разбиение отрезков
,
то x[a,b],
y[c,
d]. Каждую частичную
дугу спроектируем на оси координат,
получим разбиение отрезков
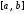 и [c, d]
на n частей; длины
частичных интервалов разбиения обозначим
соответственно хk
и yk.
Составим интегральную сумму вида:
и [c, d]
на n частей; длины
частичных интервалов разбиения обозначим
соответственно хk
и yk.
Составим интегральную сумму вида:
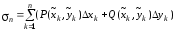 .
.
Эта
сумма представляет собой сумму
скалярных произведений векторов
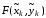 на векторы
на векторы
 ,
где
,
где
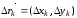 ,
т.е.
,
т.е.
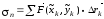
Обозначим

Определение
Если
существует
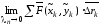 ,
не зависящий ни от способа разбиения
дуги
,
не зависящий ни от способа разбиения
дуги
 на части, ни от выбора точки
на части, ни от выбора точки
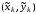 ,
то этот предел называется криволинейным
интегралом II
рода и обозначается
,
то этот предел называется криволинейным
интегралом II
рода и обозначается
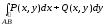 или
или
 .
.
Итак, по определению, криволинейный интеграл II рода
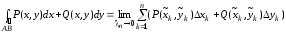 ,
,
Заметим,
что условие
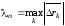 →0
равносильно условиям
→0
равносильно условиям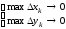
В отличие от криволинейного интеграла I рода, который еще называют интегралом по длине дуги, криволинейный интеграл II рода называют криволинейным интегралом по координатам.
Аналогично может быть дано определение криволинейного интеграла II рода по пространственной кривой
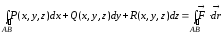
Свойства криволинейного интеграла второго рода:
1.
 ,
т.е. интеграл меняет знак
при изменении направления движения
по кривой (ориентации кривой).
,
т.е. интеграл меняет знак
при изменении направления движения
по кривой (ориентации кривой).
2. Свойство линейности:

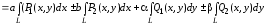 .
.
В
частности,
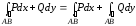
3.
Свойство аддитивности: если
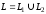 ,
то
,
то
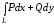 =
=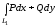 +
+
4. Связь между криволинейными интегралами I и II рода выражает формула:
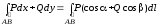 ,
,
где
(cos,
cos)
– направляющие косинусы касательной
к дуге
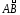 в любой ее точке.
в любой ее точке.
Физический
смысл криволинейного интеграла
II рода по дуге
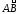 кривой
L:
кривой
L:
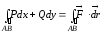
определяет
работу силы
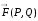 при перемещении материальной точки
вдоль кривой L
из положения А в положение В.
при перемещении материальной точки
вдоль кривой L
из положения А в положение В.
Рассмотрим замкнутую кривую C, будем называть ее замкнутым контуром. Ориентацию на этой кривой выберем следующим образом: если при движении точки М вдоль контура C ограниченная этим контуром область D остается слева, то направление движения (ориентацию на кривой C) будем считать положительным. В противном случае (область D справа) – отрицательным.


Криволинейный
интеграл II рода по
замкнутому контуру будем обозначать
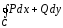
Справедлива
Теорема 1 (формула Грина)
Пусть
С – положительно
ориентированная замкнутая кривая,
ограничивающая область D,
а функции P(x,
y) и Q(x,
y) непрерывны вместе
со своими частными производными
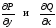 в области D и на её
границе C.
Тогда имеет место равенство
в области D и на её
границе C.
Тогда имеет место равенство
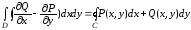 .
.
Это равенство называют формулой Грина. Она устанавливает связь криволинейного интеграла второго рода с двойным интегралом.
Заметим,
что если положить в формуле Грина
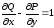 ,
то получим
,
то получим

Рассмотрим три случая:
А)
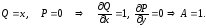 Тогда
Тогда
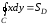 .
.
Б)
 Тогда
Тогда
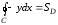 .
.
В)

Тогда
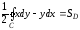 .
.
Таким образом, с помощью криволинейного интеграла II рода по замкнутому контуру С можно найти площадь области, ограниченной этим контуром:
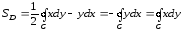
Справедливо также следующая важная теорема.
