Теорема 2.

Если функции P(x, y) и Q(x, y) непрерывны вместе со своими производными и в области D, и , то следующие утверждения эквивалентны:

1. Для любого замкнутого контура .

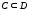
2. не зависит от пути интегрирования 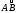, а зависит только от начальной А и конечной В его точек и обозначается .

Условие при этом называют условием независимости криволинейного интеграла от пути интегрирования.

3. Существует функция 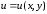такая, что а и тогда

.

Это равенство, по существу, представляет собой аналог формулы Ньютона-Лейбница для криволинейного интеграла второго рода. Если при этом А(х₀, y₀) – некоторая фиксированная точка, а В(x, y) – текущая точка области D, то

,

что означает аналог теоремы Барроу^*), где С = - u(х₀, y₀).

Таким образом, если по известному дифференциалу функции двух переменных требуется найти функцию , нужно вычислить криволинейный интеграл второго рода от выражения по любому пути, соединяющему произвольную фиксированную точку (х₀, у₀) области определения функций 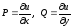и текущую точку (х, у). Очевидно, такие функции определяются с точностью до константы.

В случае функции трёх переменных и пространственной кривой L, условия независимости интеграла от пути интегрирования (или того, что есть дифференциал некоторой функции) имеют вид:

.

Способы вычисления криволинейного интеграла II рода

В зависимости от описания линии интегрирования , преобразование криволинейного интеграла второго рода к определенному интегралу может быть произведено следующими способами.

1) Если : y = (x), x  [a, b], то dy = (x)dx и

. (1)

2) Если : x = (y), y  [c, d], то dx = (y)dy и

. (2)

3) Если : , t  [,], то dx = x(t)dt, dy = y(t)dt, и тогда

. (3)

4) Если L – пространственная кривая, заданная параметрическими уравнениями , , то . Тогда

. (4)

Пример 1

Вычислить , где 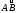– дуга параболы от точки с абсциссой до точки с абсциссой .

Решение: Поскольку линия интегрирования задана условиями , , то используем принцип перехода к определенному интегралу, указанный выше в пункте 1 (формула (1)):

.

Пример 2

Вычислить , где – отрезок прямой между точками А(2, –2, 0) и В(1, 1, 1).

Решение: Найдем уравнение прямой, проходящей через точки А и В:

При этом точке А(2, –2, 0) соответствует значение , а точке В(1, 1, 1) – значение , значит, на линии .

Таким образом, имеем случай задания линии интегрирования, рассмотренный выше в пункте 4 (формула (4)). Тогда

.

Пример 3.

Вычислить , если L – контур треугольника с вершинами , B(3,1), C(1,5), пробегаемый против часовой стрелки.

Решение.

Треугольник АВС, по которому идет интегрирование, изображен на рисунке 1. Как видим, контур L этого треугольника состоит из трех участков: АВ, ВС и СА. Эти отрезки лежат на разных прямых, и, следовательно, задаются разными уравнениями. Поэтому сначала необходимо воспользоваться свойством аддитивности криволинейного интеграла и расписать его в виде суммы трех интегралов по соответствующим отрезкам:

.

Вычислим каждый из этих интегралов отдельно. При этом обязательно нужно учитывать, что движение по контуру – против часовой стрелки: АВСА (кстати, это означает, что контур ориентирован положительно).

Отрезок AB имеет уравнение y=1, x[1,3], следовательно (формула (1))

.

Рассмотрим отрезок ВС. Найдем сначала уравнение прямой, проходящей через точки и :

.

Таким образом, уравнение отрезка BC имеет вид , а так как обход контура осуществляется против часовой стрелки (т.е. движение вдоль этого отрезка происходит от точки B к точке C), то переменная x меняется от 3 до 1. Тогда (снова формула (1)) получим

.

Отрезок CA определяется уравнением x=1 (т.е. уравнение вида x = (y), используем формулу (2)) направление движения вдоль этого отрезка от точки C к точке A, значит, переменная y меняется от 5 до 1. Поэтому соответствующий интеграл равен

.

Тогда заданный интеграл равен

.

Пример 4.

Вычислить , если L – первая арка циклоида

Решение. Очевидно, заданный интеграл есть криволинейный интеграл II рода:

.

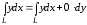Циклоида имеет вид, изображённый на рис.2. Первая арка циклоиды расположена в первой четверти и соответствует изменению параметра t от 0 до 2π. Поскольку линия L задана параметрическими уравнениями, то криволинейный интеграл II рода сводиться к определённому по формуле (3). Тогда получаем

.

Пример 5.

Доказать, что не зависит от пути интегрирования L, и вычислить его по линии, соединяющей точки A(1,2) и С(2,1).

Решение.

Согласно теореме 2 (стр.4), чтобы криволинейный интеграл по координатам не зависел от пути интегрирования L, необходимо и достаточно, чтобы в некоторой области D, содержащей линию L, функция P(x,y) и Q(x,y) вместе со своими частными производными и были непрерывны и выполнялось условие .

В нашем случае , . Тогда имеем

И сами функции 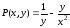, , и их частные производные, очевидно, непрерывны на всей плоскости хOу, кроме точек, лежащих на прямых x=0 и y=0. Значит, заданный криволинейный интеграл действительно не зависит от пути интегрирования, поэтому для его вычисления можно взять любую кривую, соединяющую точки A и B и не пересекающую прямые x=0 и y=0 (т.е. оси координат).

В таких случаях проще всего криволинейный интеграл II рода вычислять по ломанной, звенья которой параллельны осям координат.

Рассмотрим ломанную ABC (рис.3), звенья которой имеют уравнения:

AВ: x=1, здесь y изменяется от 2 до 1,

BC: y=1, здесь x изменяется от 1 до 2.

Тогда имеем

=

.

Здесь воспользовались свойством определенного интеграла о независимости интеграла от переменной интегрирования.

Но, поскольку интеграл не зависит от пути интегрирования, то можно выбрать и любую другую линию, соединяющую точки А и С. Рассмотрим, например, прямую АС. Её уравнение:

.

При перемещении по этой прямой от точка А к точке С переменная у меняется от 2 до 1. Тогда получим

.