Пример 6.
Вычислить
 .
.
Решение.
Данный
интеграл есть криволинейный интеграл
второго рода (по координатам), который
нужно вычислить вдоль некоторой линии
от точки
 до
точки
до
точки
 .
Поскольку линия не задана, то можно
предположить, что данный интеграл не
зависит от пути интегрирования. Проверим
это.
.
Поскольку линия не задана, то можно
предположить, что данный интеграл не
зависит от пути интегрирования. Проверим
это.
Здесь
 ,
,
 ,
,
 .
Очевидно и сами функции, и их производные
непрерывны на всей числовой плоскости
и выполняется условие
.
Очевидно и сами функции, и их производные
непрерывны на всей числовой плоскости
и выполняется условие
 .
Значит, действительно, интеграл не
зависит от вида кривой, а зависит только
от точек А(1; 1) и В(3; 5). Следовательно,
можно выбрать любую линию, их соединяющую.
.
Значит, действительно, интеграл не
зависит от вида кривой, а зависит только
от точек А(1; 1) и В(3; 5). Следовательно,
можно выбрать любую линию, их соединяющую.
Рассмотрим
прямую, проходящую через точки А и
В:

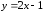 .
.
Тогда
получим


 .
.
Пример 7.
Вычислить
 .
.
Решение:
Рассматривается криволинейный
интеграл второго рода по замкнутому
контуру. Контур С есть окружность
радиуса 1 с центром в начале координат
(рис. 4). Применим формулу Грина (стр.3).
При этом контур С ограничивает
область D, которая
представляет собой, очевидно, круг
 .
.

В
данном интеграле
 ,
,
 .
Тогда
.
Тогда
 ,
,
 .
По формуле Грина получаем
.
По формуле Грина получаем
 .
.
Здесь
мы используем свойство двойного интеграла
 .
.
Пример
8.
Найти
функцию
 по ее дифференциалу
по ее дифференциалу
 .
.
Решение:
Согласно теореме 2 (стр.4), по
известному полному дифференциалу
функции двух переменных можно найти
саму эту функцию с помощью криволинейного
интеграла второго рода от заданного
дифференциала:
 .
.
Но
для этого необходимо, чтобы выполнялось
условие независимости интеграла от
пути интегрирования. Убедимся в этом.
Пусть
 ,
,
 .
Очевидно, эти функции непрерывны на
всей числовой плоскости. Находим
.
Очевидно, эти функции непрерывны на
всей числовой плоскости. Находим
 ,
,
 ,
следовательно
,
следовательно
 – условия независимости интеграла от
пути интегрирования выполняются.
– условия независимости интеграла от
пути интегрирования выполняются.
В
качестве линии интегрирования выберем
ломаную АСВ (рисунок 5), где
 –
произвольная фиксированная
точка плоскости,
–
произвольная фиксированная
точка плоскости,
 –
текущая точка плоскости.
Отрезки АС и СВ параллельны осям Ох
и Оу соответственно.
–
текущая точка плоскости.
Отрезки АС и СВ параллельны осям Ох
и Оу соответственно.
Тогда








 ,
,
где
 .
.
Если
взять (х0, y0)
= (0, 0), получим:
 .
.
*)*)
Теорема Барроу: Если f(х)
непрерывна на отрезке [a,
b], то для любого х[a,
b] функция Ф(х)=
дифференцируема на [a,
b] и Ф(х)
= f(х). Т.е. интеграл
с переменным верхним пределом есть
первообразная для подынтегральной
функции.
14


 .
. до
точки
до
точки
 .
Поскольку линия не задана, то можно
предположить, что данный интеграл не
зависит от пути интегрирования. Проверим
это.
.
Поскольку линия не задана, то можно
предположить, что данный интеграл не
зависит от пути интегрирования. Проверим
это. ,
,
 ,
,
 .
Очевидно и сами функции, и их производные
непрерывны на всей числовой плоскости
и выполняется условие
.
Очевидно и сами функции, и их производные
непрерывны на всей числовой плоскости
и выполняется условие
 .
Значит, действительно, интеграл не
зависит от вида кривой, а зависит только
от точек А(1; 1) и В(3; 5). Следовательно,
можно выбрать любую линию, их соединяющую.
.
Значит, действительно, интеграл не
зависит от вида кривой, а зависит только
от точек А(1; 1) и В(3; 5). Следовательно,
можно выбрать любую линию, их соединяющую.
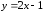 .
.

 .
. .
.
 .
.

 ,
,
 .
Тогда
.
Тогда
 ,
,
 .
По формуле Грина получаем
.
По формуле Грина получаем .
.
 .
.
 по ее дифференциалу
по ее дифференциалу
 .
. .
. ,
,
 .
Очевидно, эти функции непрерывны на
всей числовой плоскости. Находим
.
Очевидно, эти функции непрерывны на
всей числовой плоскости. Находим
 ,
,
 ,
следовательно
,
следовательно
 – условия независимости интеграла от
пути интегрирования выполняются.
– условия независимости интеграла от
пути интегрирования выполняются. –
произвольная фиксированная
точка плоскости,
–
произвольная фиксированная
точка плоскости,
 –
текущая точка плоскости.
Отрезки АС и СВ параллельны осям Ох
и Оу соответственно.
–
текущая точка плоскости.
Отрезки АС и СВ параллельны осям Ох
и Оу соответственно.








 ,
, .
. .
.