Краткая теория

При взаимодействии электромагнитного излучения с веществом монохроматическое излучение с частотой ведет себя как совокупность одинаковых частиц – фотонов, энергия которых равна

, (1)

где Джс. Масса фотона определяется в соответствии с теорией относительности и законом взаимосвязи массы и энергии, согласно которому

. (2)

Поэтому , следовательно

. (3)

Импульс фотона связан с его энергией соотношением

(4)

и его можно определить как

. (5)

Приведенные формулы связывают корпускулярные характеристики фотона (энергия, масса, импульс) с его волновыми характеристиками (длиной волны, частотой) и доказывают двойственную природу света.

Квантовые свойства света отчетливо проявляются в эффекте, который наблюдал А. Комптон в 1923 году при исследовании рассеяния рентгеновских лучей в парафине. Схема его эксперимента изображена на рис. 1. Пучок монохроматического рентгеновского излучения падает на «легкое», рассеивающее вещество (парафин) и после рассеяния под углом попадает в приемник – рентгеновский спектрограф, где измеряется длина волны рассеянного излучения. Опыты показали, что в составе рассеянного излучения наряду с излучением первоначальной длины волны появляется длинноволновое излучение.

Объяснение эффекта Комптона дано на основе квантовых представлений, как упругое столкновение двух частиц: налетающего фотона, обладающего импульсом и энергией, с покоящимся свободным электроном (энергия покоя,– масса покоя электрона).

В каждом акте соударения фотон передает часть своей энергии и импульс электрону и изменяет направление движения – рассеивается. Уменьшение энергии фотона означает увеличение длины волны рассеянного света. Электрон, получивший от фотона энергию и импульс, приходит в движение (испытывает отдачу). Этот электрон называется электроном отдачи. При каждом столкновении фотона и свободного электрона выполняются закон сохранения энергии:

(6)

и закон сохранения импульса:

. (7)

Выражение (7) с учетом правила сложения векторов импульса будет иметь вид:

, (8)

где – импульс рассеянного фотона.

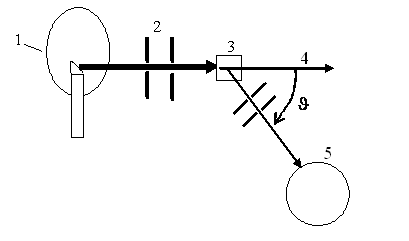
Рис. 1. Схема эксперимента: 1– рентгеновская трубка, 2 – диафрагмы, 3 – парафин, 4 – прошедшее излучение, 5 – рассеянное излучение

Совместно решая уравнения (6) и (8) и учитывая, что , получим выражение

, (9)

где м – комптоновская длина волны электрона.

Из выражения (9) видно, что сдвиг световой волны не зависит от длины волныпадающего света и от природы рассеивающего вещества, а определяется углом рассеяния фотона. Наибольшее увеличение длины волны происходит при= 180°, когда фотон рассеивается в сторону, противоположную первоначальному направлению его движения (). Скорость электрона при отдаче может быть очень большой. Энергия электрона после столкновения будет. В случае эффекта Комптона в рассеянном излучении наряду со смещенной линией наблюдается несмещенная линия. Эта линия связана с тем, что в реальных опытах по рассеянию фотонов веществом электроны не свободны, а связаны в атомах. Поэтому фотон отдает энергию атому в целом, т. к. масса атома много больше массы электрона. Комптоновское смещение в этом случае ничтожно, ипрактически совпадает с. С увеличением атомного номера химического элемента увеличивается относительное число атомов с сильной связью, что обусловливает ослабление смещенной линии. Поэтому эффект Комптона не может наблюдаться в видимой области спектра, т. к. в этом диапазоне длин волн, что практически невозможно обнаружить, поскольку изменение длины волны по порядку величины равно линии излучения атомов, в то время как для рентгеновских фотонов. Кроме того, энергия фотона видимого света сравнима с энергией связи электрона с атомом, следовательно, даже внешний электрон нельзя считать свободным.

Эффект Комптона наблюдается и на других заряженных частицах, например на протонах. Эффект Комптона, как и фотоэффект, происходит при взаимодействии фотона с электронами. Однако, эффект Комптона обусловлен рассеянием фотона на свободных или слабосвязанных электронах, а фотоэффект – поглощением фотонов связанными электронами.