Тема 3(2)

ответом на стратегию второго, и то же выполнялось бы и для его соперника. Однако это не так.

Предположим, что второй игрок случайно выбирает одну из трех возможных стратегий, то есть вероятности выбора стратегий «Камень», «Ножницы» или «Бумага» соответственно равны 1/3 каждая.

Поскольку мы знаем, что игроку I безразлично, что играть, можно утверждать, что он может играть как угодно, что точно не принесет ему проигрыш. Он может выбрать стратегию случайно выбирать какую-либо стратегию равными вероятностями 1/3. Проше всего представить процесс его выбора подбрасыванием кубика, обладающего 6 гранями, две из которых будут соответствовать выбору первым игроком камня, 2 – ножниц и 2 – бумаги.

Отсутствие в игре равновесия Нэша в чистых стратегиях не означает, что в игре нет равновесия Нэша как такового.

Предпосылки для использования равновесия Нэша в смешанных стратегиях:

1)Равновесие Нэша в смешанных стратегиях стоит искать, если в игре есть больше одного равновесия в чистых стратегиях (например, в игре «Битва Полов»). Оно будет сыграно, если у участников нет возможности договориться о том, какое равновесие играть.

2)Равновесие Нэша в смешанных стратегиях будет играться в случае отсутствия равновесия Нэша в чистых стратегиях (например, в играх «Инспектирование» и «Орел или Решка»), так как, во-первых, оно существует и будет единственным; во-вторых, мы запутаем соперника так, чтобы он не смог помешать нам получить больший выигрыш.

«Орел или Решка» («Matching Pennies»)

Вданной игре (а это, кстати, игра с нулевой суммой) принимают участие два игрока, которые независимо друг от друга называют одну из сторон монеты: орла или решку. Если оба игрока выбрали одно и то же, то первый игрок выигрывает, а второй, соответственно, проигрывает. Если участники назвали разные стороны, то игрок II выигрывает, тогда как игрок I считается проигравшим.

Вматричном виде игру можно представить следующим образом:

II

ОР

Играть какую-либо определенную (чистую) стратегию в такой игре – не такая уж и хорошая идея. Если второй игрок выбирает стратегию «Орел», у игрока I появится мотив ответить стратегией «Орел», чтобы заполучить выигрыш «1». В этом случае второй игрок выберет стратегию «Решка», которая принесет ему выигрыш «1». Далее игрок I сменит стратегию, что принесет ему выигрыш «1». Тогда второй игрок вернется к стратегии «Орел» и так далее. Здесь нет ни одного профиля стратегий, который удовлетворял бы обоих участников. Имеет смысл запутать соперника, играя случайно: выбирая не конкретную стратегию, а подбросив монетку. Что выпадет, то и стоит играть.

Мы играем равновесие в смешанных стратегиях для того, чтобы соперник нас не обыграл. Запутываем его, чтобы сделать безразличным к его чистым стратегиям.

q

1

1/2

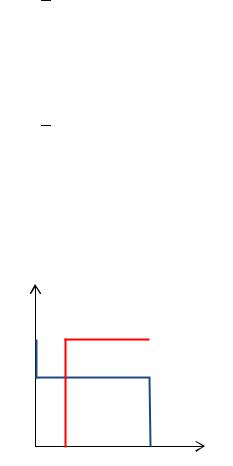
В данной антагонистической игре выбор { } в ответ на { } (то есть играть случайно) –

это лучший ответ, значит .{ } { }/ - это равновесие Нэша.

Здесь равновесие Нэша в смешанных стратегиях позволяет запутать соперника так, чтобы он не смог помешать нам получить больший выигрыш (в чем и заключается вторая предпосылка). Равновесие Нэша в смешанных стратегиях здесь – своего рода точка переключения между чистыми стратегиями. Если играть какую-либо чистую стратегию с определенной частотой, то соперник может догадаться и выбирать стратегию, которая принесет ему наибольший выигрыш, а если строго смешивать по 1/2, то догадаться, что лучше играть, невозможно.

Налогоплательщик

ЧНЧ

Мы уже выяснили, что равновесие Нэша в игре не всегда можно найти на матрице игры. Теорема Нэша о существовании гласит, что равновесие Нэша есть всегда, быть может в области смешанных стратегий. В более обобщенном виде она звучит так: любая конечная игра содержит равновесие Нэша. Это означает, что игра, в которой множество равновесий Нэша в чистых стратегиях отсутствует, обязательно содержит равновесие Нэша в смешанных стратегиях. Найдем его.

Выбираем такое смешение, чтобы соперник нас не обыграл.

q

1

РНСС

2/3

В отличие от предыдущего случая, где равновесие Нэша в смешанных стратегиях позволяло переключаться между чистыми стратегиями, в этой игре оно содержит еще и другую интерпретацию: это своего рода доли, с которыми будут сыграны чистые стратегии в популяции. Представим город с населением 210 человек, каждый из них - налогоплательщик. Часть из них предпочитают честно уплачивать налоги, тогда как

избегать.

Регулятор (государство) хотел бы, чтобы в данном городе честных налогоплательщиков было больше. Обычная мера для этого - увеличим штраф за неуплату налогов с «-10» до «- 20».

Налогоплательщик

ЧНЧ

Мы наблюдаем уменьшение p, что говорит о том, что вероятность проверки инспектором документов налогоплательщика снизится. Однако q остается неизменным, следовательно, увеличение штрафа не приведет к увеличению честности.

Вывод: изменение выигрыша одного игрока ведет к изменению равновесия в смешанных стратегиях другого игрока, и только его. Чтобы поменять равновесие одного игрока, необходимо сменить выигрыши другого.

В рамках этой задачи увеличение честности среди налогоплательщиков последует в том случае, если мы увеличим выигрыш инспектора в (П; НЧ), т.е. увеличим его премию за поимку нечестного налогоплательщика:

Налогоплательщик

ЧНЧ

Источник изображения – веб-комикс XKCD.

«Семейный Спор #1»/«Битва Полов» («Battle of Sexes»)

Участники этой игры – муж и жена – решают, как им следует провести вечер. Обсуждаются два варианта: футбол и театр. При этом они хотят быть вместе: если они пойдут в разные места, то вечер пропадет. Решения участниками принимаются одновременно. Матрица выигрышей выглядит следующим образом:

Ж

ФТ

Множество равновесий Нэша в чистых стратегиях: (Ф; Ф), (Т; Т).

Это классический пример координационной игры: сразу видно, что существуют два равновесия в чистых стратегиях. Актуальна первая предпосылка использования равновесия Нэша в смешанных стратегиях: его стоит искать, если в игре есть больше одного равновесия в чистых стратегиях, и оно будет сыграно, если у участников нет возможности договориться о том, какое равновесие играть.

{}

{}

Равновесие Нэша в смешанных стратегиях: ( ) = ({ } { }).

В этой игре лучше согласиться на плохое равновесие, нежели чем подумать о разных. Если все же не получается понять, какое равновесие будет сыграно, то необходимо сделать супруга безразличным.

Любое другое смешение чистых стратегий мужем принесет ему выигрыш также равный .

Таким образом, желания отклониться от равновесия у него не будет. Аналогичное соотношение выигрышей можно показать и для жены.

Опишем лучшие ответы игроков:

График лучших ответов предполагает пересечение лучших ответов в 3 точках, т.е доказывает, что равновесий здесь действительно 3, как и в аналитическом решении.

q

1

РНЧС (Ф; Ф)

1/3 РНСС

Рассмотрим менее тривиальные случаи матричных игр, например, когда у каждого из игроков по три чистые стратегии:

РНЧС: (C; D).

Чтобы найти множество равновесий Нэша в смешанных стратегиях, необходимо найти из условия, что выигрыши игрока от всех его чистых стратегий в ответ на найденное

смешение соперника будут равны. Для этого нужно решить следующую систему:

(при )

( )

. /

(при )

( )

( )