3. Метод золотого сечения

Одним из наиболее эффективных методов, в которых при ограниченном количестве вычислений f(x) достигается наилучшая точность, является метод золотого сечения. Он состоит в построении последовательности отрезков [ао,Ьо],[a1,b1],... , стягивающихся к точке минимума функции f(x). На каждом шаге, за исключением первого, вычисление значения функции f(x) проводится лишь в одной точке. Эта точка, называемая золотым сечением.

Идея метода(геометрически)

Внутри отрезка [ао,bо] выбираем некоторые внутренние точки х1 и Х2 и вычисляем значения целевой функции f(x1) и f(x2). Поскольку f(x1) < f(x2), очевидно, что минимум расположен на одном из прилегающих к х1 отрезков: [ao,x1] или [x1,x2]. Поэтому отрезок [x2,Ьо] можно отбросить, сузив тем самым первоначальный интервал неопределённости.

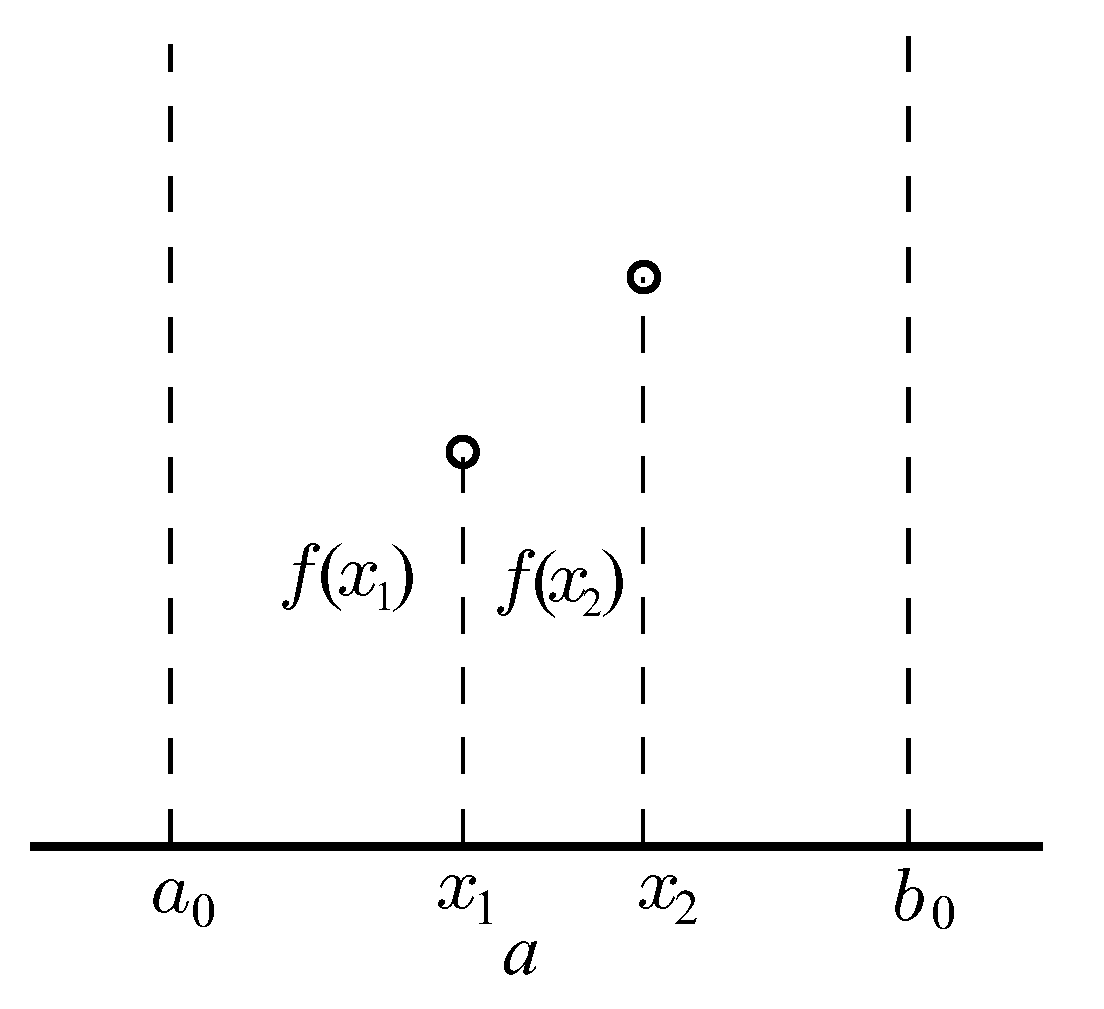
Далее проводим на отрезке [а1, b1] где а1 = а0, Ь1 = = Х2. Нужно снова выбрать две внутренние точки, но одна из них (х1) осталась из предыдущего шага, поэтому достаточно выбрать лишь одну точку х3, вычислить значение f(x3) и провести сравнение.

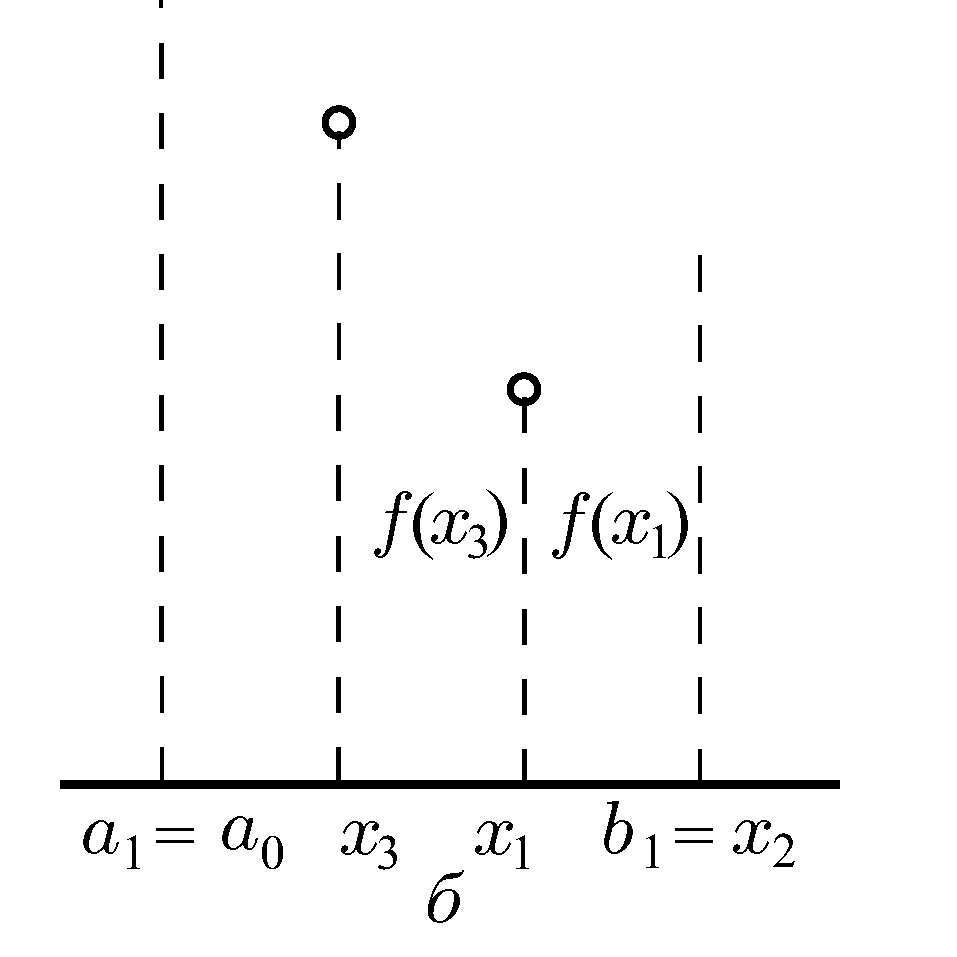
f(х3) < f(x1), значит минимум находится на отрезке [x3, b1]. Обозначим

этот отрезок [a2,b2], снова выберем одну внутреннюю точку и повторим процедуру сужения интервала неопределенности. Процесс оптимизации повторяется до тех пор, пока длина очередного отрезка [ak,bk] не станет меньше заданной величины е.

Способ размещения внутренних точек на каждом отрезке.

Пусть длина интервала неопределенности равна l, а точка деления разбивает его на части l1, l2: l1 > l2, I = l1 + l2. Золотое сечение интервала неопределенности выбирается так, чтобы отношение длины большего отрезка к длине всего интервала равнялось отношению длины меньшего отрезка к длине большего отрезка:

Преобразуем это выражение и найдем значения

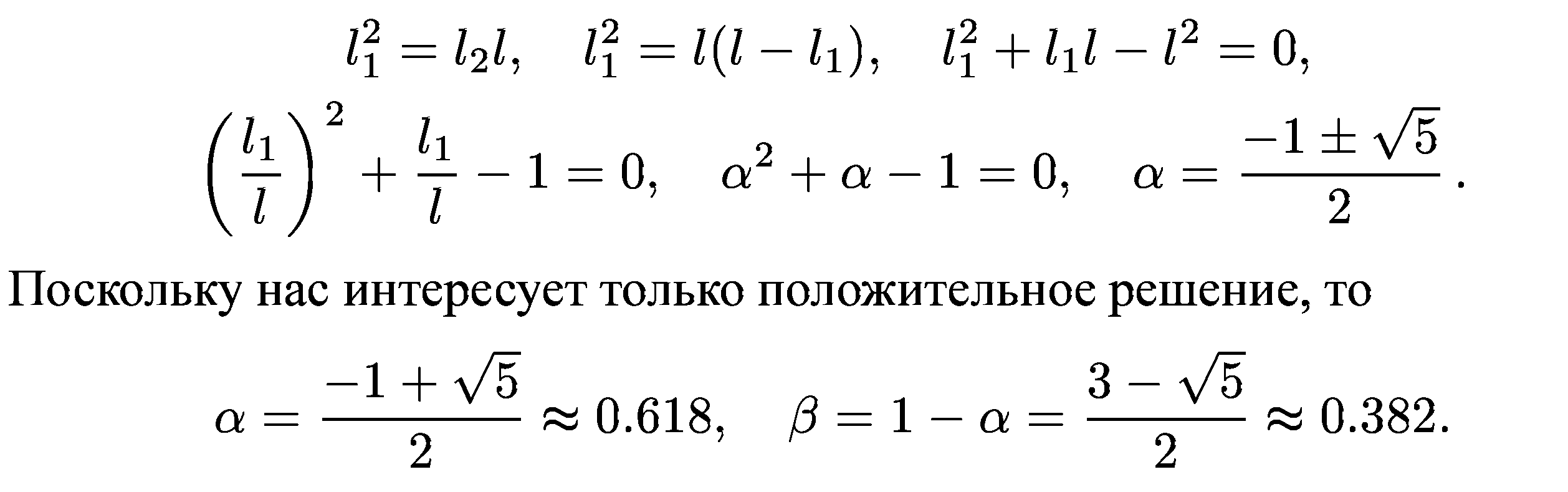
Интервал неопределенности можно разделить в соотношении золотого сечения двояко: в пропорциях I2 : l1 и l1 : l2. Имеем:

Алгоритм процесса одномерной оптимизации методом золотого сечения:

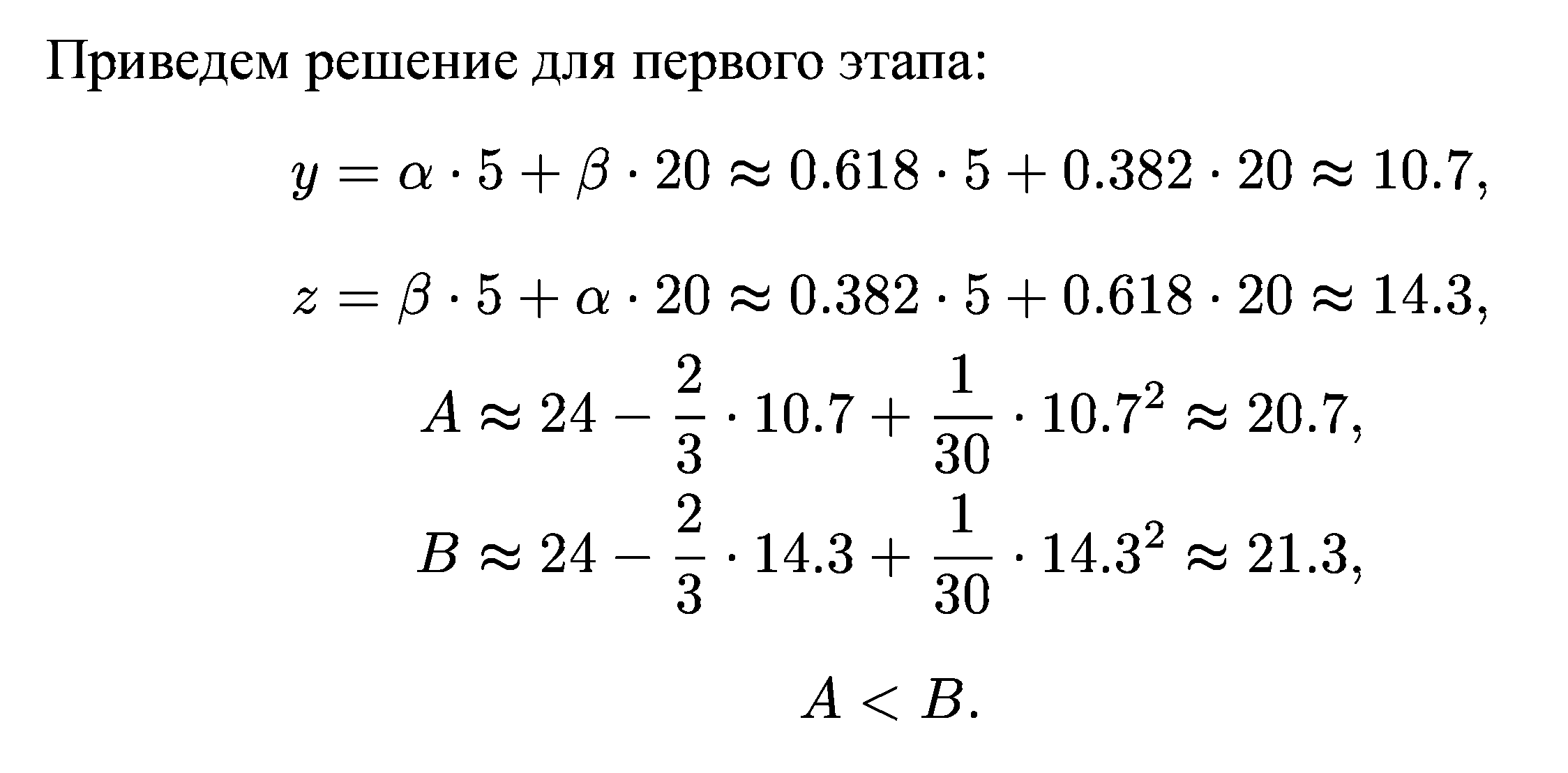
4. Метод Ньютона

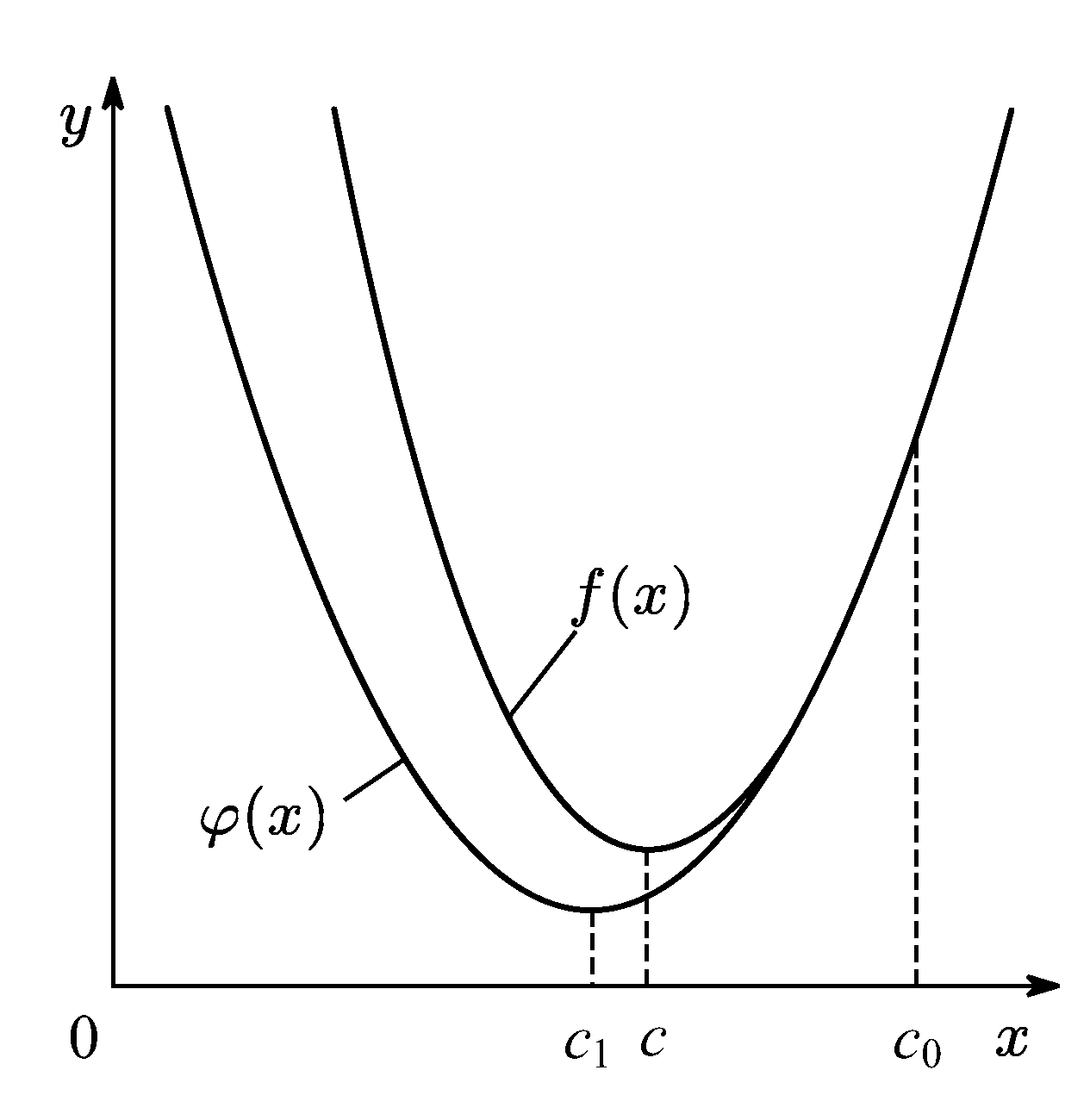
Пусть х = с — решение уравнения f’(x), а с0 — некоторое начальное приближение к с. Применим метод Ньютона решения уравнения F(x) = 0, которое эквивалентно уравнению при F(x) =f' (х). Для этого в формулу для к-то приближения метода Ньютона подставим вместо F(x) производную f'(x) и получим тем самым формулу для к-то приближения к решению уравнения:

Для использования этой формулы необходимо, чтобы:

Достаточные условия сходимости метода Ньютона:

последовательность значений

Точка x=c может являться и точкой минимума, и точкой максимума, а может вообще не являться точкой экстремума.

Метод Ньютона обладает более быстрой сходимостью, чем методы, которые не используют дифференциальные свойства функции. Но сходимость не гарантирована, если не удачно выбрать начальное приближение. Пример.

23. Метод покоординатного спуска.

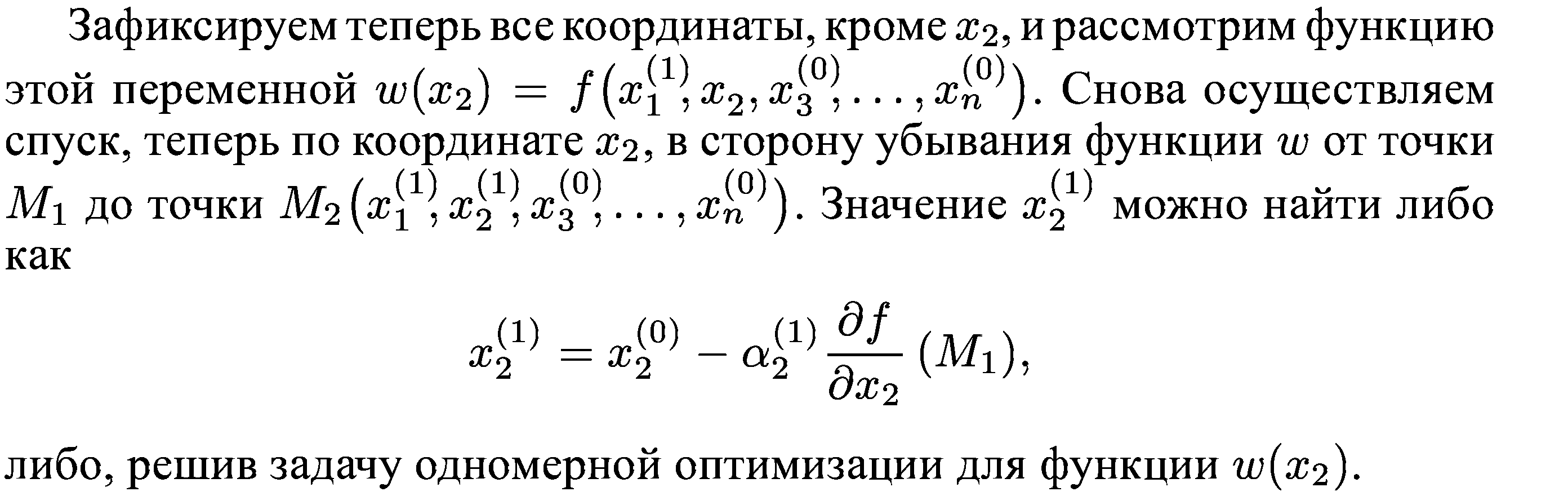
Метод покоординатного спуска сводит задачу о нахождении наименьшего значения функции многих переменных к многократному спуску в сторону уменьшения значений функции по каждому проектному параметру. Данный метод легко проиллюстрировать геометрически для случая функции двух переменных z = f(x,y), описывающей некоторую поверхность в трехмерном пространстве.

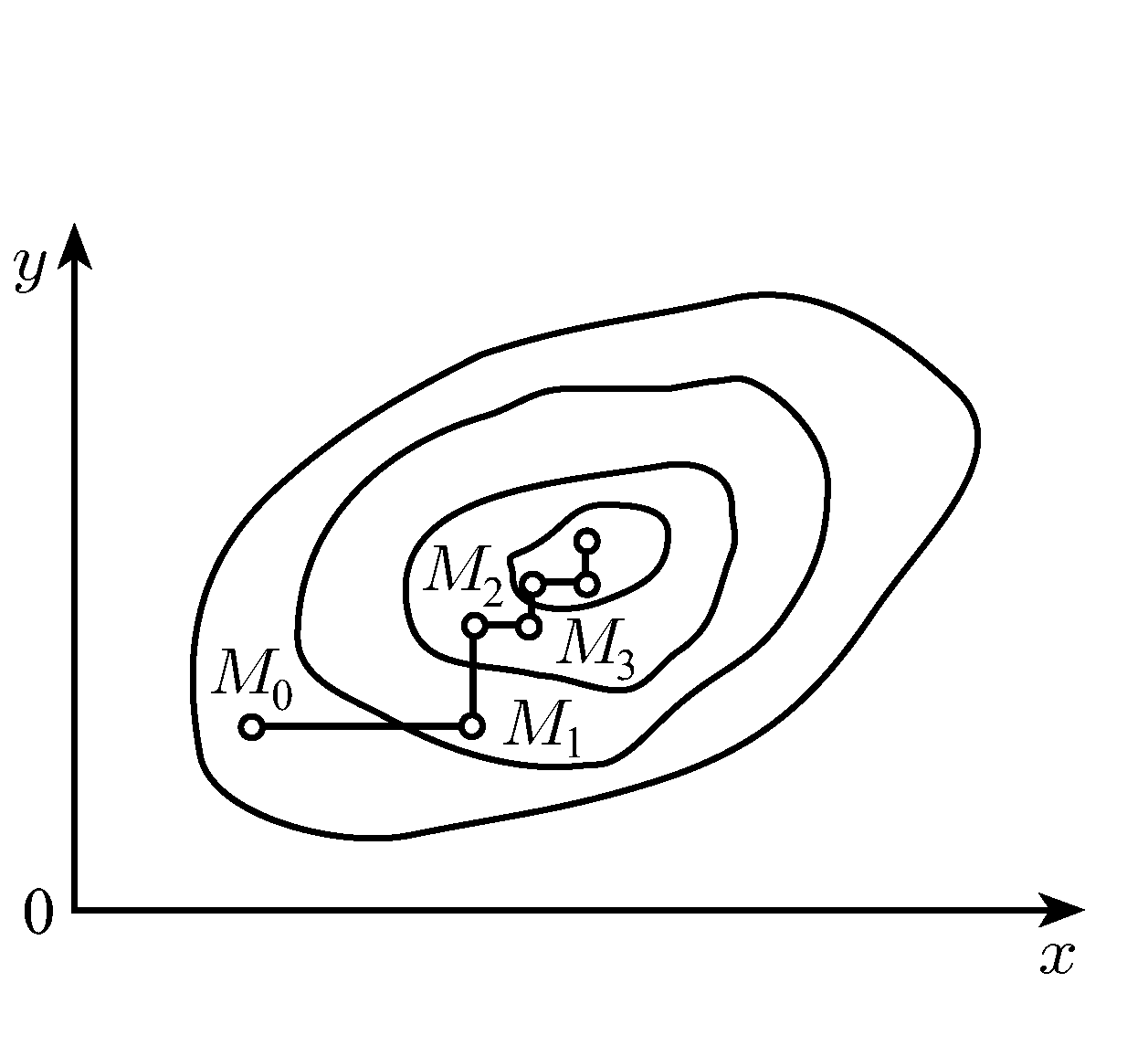
Процесс оптимизации в этом случае проходит следующим образом. Точка М0(x0,y0) описывает начальное приближение. Проводя спуск по координате х, попадем в точку M1(x1,y0). Далее, двигаясь параллельно оси ординат, придем в точку М2(x1,y1) и т. д.

Для функции двух переменных очевидно, что метод может оказаться неприменимым при наличии изломов в линиях уровня. Для гладких функций при удачно выбранном начальном приближении (в некоторой окрестности минимума) процесс сходится к минимуму. Здесь однако применение метода затруднено в случае так называемых оврагов на поверхности. Овраг представляет собой впадину, линии уровня которой имеют форму овалов с различающимися во много раз длинами осей.

Пример оврага

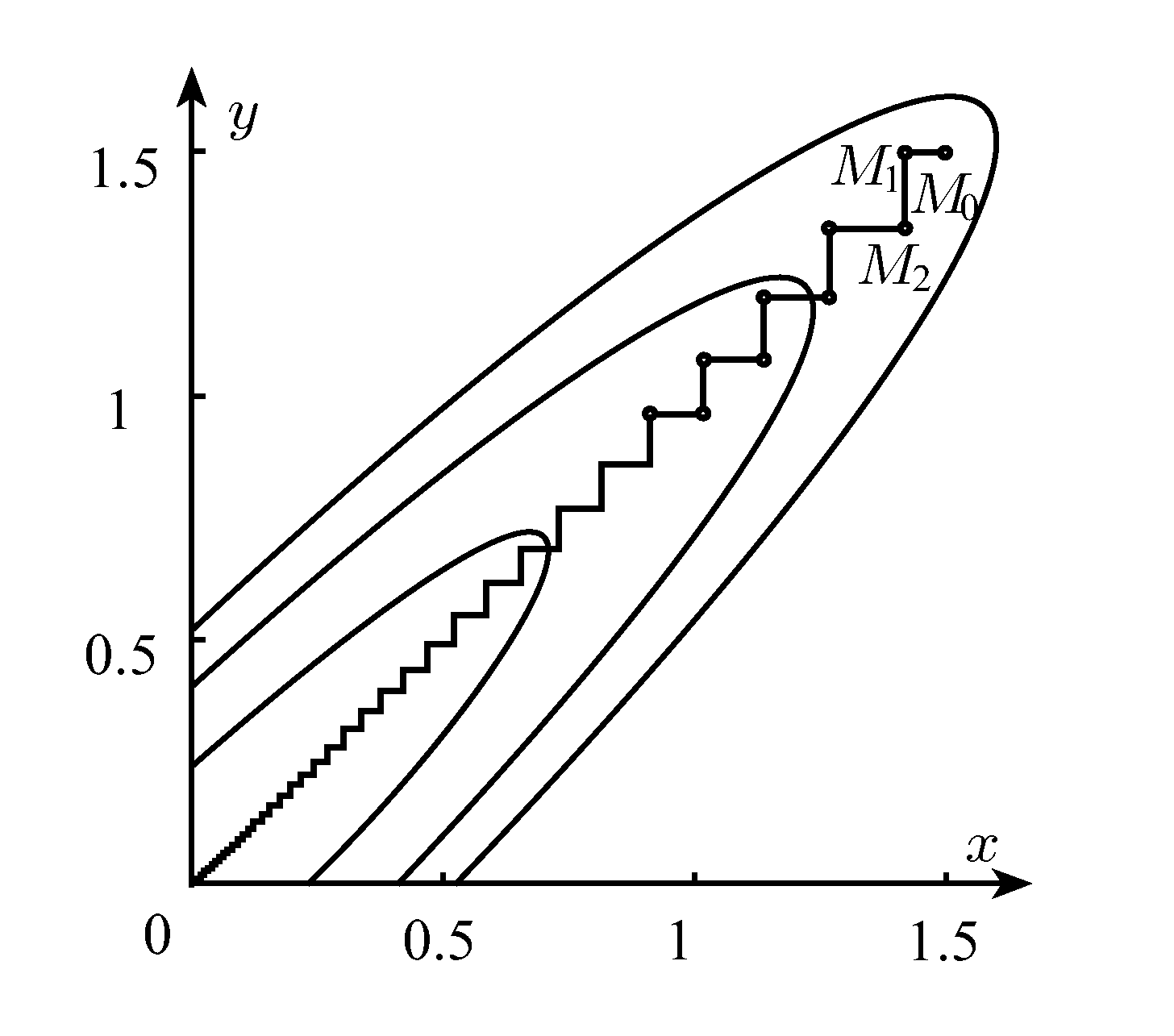
изображены линии уровня функции, которую поворотом системы координат можно

привести к виду z = х^2 + З6у^2. Точкой минимума этой функции является начало координат. Наличие оврага приводит к тому, что процесс спуска к минимуму очень длительный, метод сходится медленно. Так при начальном приближении х = у = 1.5 после 50 итераций получается приближение х~ у ~ 0.006.

К достоинствам метода покоординатного спуска следует отнести возможность использования простых алгоритмов одномерной оптимизации. Структурограмма метода покоординатного спуска представлена на рисунке:

Итерации завершаются при выполнении условия: