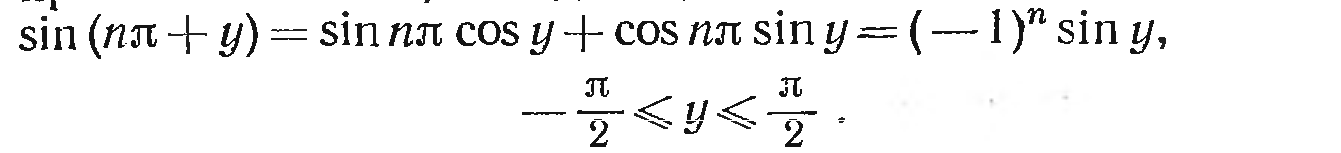Vychislitelnaya_matematika / Vychislitelnaya_matematika / Вычислительная математика / 1-5

Вычислительная математика

1. Математическая модель, численный метод, вычисления. Погрешности.

Объект исследования

↓

Математическая модель

↓

Численный метод(дискретная модель, вычислительный алгоритм)

↓

Компьютерная программа

На каждом этапе возникают ошибки. Каждая стрелка дает нам некоторую погрешность.

Математика изучает математические модели.

О

• Описание с помощью математической модели

бъект

Процесс

Основное требование, предъявляемое к математической модели,- адекватность рассматриваемому явлению, т.е. она должна достаточно точно( в рамках допустимых погрешностей) отражать характерные черты явления. Вместе с тем она должна обладать сравнительной простотой и допустимостью исследования.

Так же есть еще одно требование- простота.

Пример!

Пусть в начальный момент времени t=0 тело, находящееся на высоте h0, начинает двигаться вертикально вниз с нач.скоростью v0. Требуется найти закон движения тела , т.е. построить математическую модель, которая позволила бы математически описать данную задачу и определить параметры движения в любой момент времени. Прежде чем строить указанную модель , нужно принять некоторые допущения , если они не заданы. В частности, предположим, что данное тело обладает средней плотностью, значительно превышающей плотность воздуха, а его форма близка к шару. В этом случае можно пренебречь сопротивлением воздуха и рассматривать свободное падение тела с учетом ускорения g. Соответсвующие соотношения для высоты h и скорости v в любой момент времени t хорошо известны из школьного курса физики. Они имеют вид:

H=h0-v0t-(gt^2)\2 v=v0+gt (1)

Эти формулы являются искомой математической моделью свободного

падения тела. Область применения данной модели ограничена случаями,

в которых можно пренебречь сопротивлением воздуха. Во многих зада-

задачах о движении тел в атмосфере планеты модель (1) не может быть

использована, поскольку при ее применении мы получили бы неверный

результат. К таким задачам относятся движение капли, вход в атмосферу

тел малой плотности, спуск на парашюте и др. Здесь необходимо постро-

построить более точную математическую модель, учитывающую сопротивление

воздуха. Если обозначить через F(t) силу сопротивления, действующую

на тело массой га, то его движение можно описать с помощью уравнений

m(dv\dt)=mg-F(t), dh\dt= -v (2)

К этой системе уравнений необходимо добавить начальные условия при

t = 0:

v = v0, h=h0 (3)

Соотношения (2) и (3) являются математической моделью для

задачи движения тела в атмосфере.

Адекватность и сравнительная простота модели не исчерпывают

предъявляемых к ней требований. Обратим еще внимание на необходи-

необходимость правильной оценки области применимости математической моде-

модели. Например, модель свободно падающего тела, в которой пренебрегают

сопротивлением воздуха, весьма эффективна для твердых тел с большой

средней плотностью и формой поверхности, близкой к сферической. Вме-

Вместе с тем в ряде других случаев (движения капельки жидкости, парашют-

парашютного устройства и др.) для решения задачи уже недостаточно известных

из курса физики простейших формул. Здесь необходимы более сложные

математические модели, учитывающие сопротивление воздуха и другие

факторы.

Численные методы. С помощью математического моделирования решение научно-технической задачи сводится к решению математической задачи, являющейся ее моделью. Для решения математических

задач используются следующие основные группы методов: аналитические, графические и численные.

При использовании аналитических методов решение задачи удается

выразить с помощью формул.

Графические методы позволяют в ряде случаев оценить порядок

искомой величины. Основная идея этих методов состоит в том, что

решение находится путем геометрических построений.

Основным инструментом для решения сложных математических задач

в настоящее время являются численные методы, позволяющие свести ре-

решение задачи к выполнению конечного числа арифметических действий

над числами; при этом результаты получаются в виде числовых значений.

Подчеркнем важные отличия численных методов от аналитических.

Во-первых, численные методы позволяют получить лишь приближенное

решение задачи. Во-вторых, они обычно позволяют получить лишь

решение задачи с конкретными значениями параметров и исходных данных.

численные методы незаменимы сложных задачах, которые не допускают аналитического решения.

Численный метод наряду с возможностью получения результата за

приемлемое время должен обладать и еще одним важным качеством —

не вносить в вычислительный процесс значительных погрешностей.

Откуда берется погрешность? От округления!

1=0.99(9)

5х+7у=12 х=1.

7х+10у=17 у=1.

х=2.415 5х+7у=12.075

у=0 7х+10у=16.905

+ Некорректное использование мат. Модели

+ исходные данные (неустранимые погрешности) Хотя бы одинаковой точности

+ численный метод. Здесь погрешность можно регулировать

+ перевод чисел из одной системы в другую

Понятие погрешности. Различают два вида погрешностей —

абсолютную и относительную. Абсолютная погрешность некоторого числа

равна разности между его истинным значением и приближенным значени-

значением, полученным в результате вычисления или измерения. Относительная

погрешность — это отношение абсолютной погрешности к приближенно-

приближенному значению числа.

(или еще так: Абсолютная ошибка- это разность между истинным и точным значением(это из тетради))

Абсолютная: Ех=Х-х0

Х=х0+Ех

Относительная: Ix=Ex\x0

Где х0- приближенное значение

Число может быть с фиксированной или плавающей точкой:

1. А=±a_na_n-1…a₁a₀,a-₁a_-2

2. A=±0,a₀a₁,a₂…10^r=a₀,a₁…a_n…*10^r-1, где a₀≠0

=> 21,0134(9) погрешность 0.0005

Но!!! 0.210134(9)*10² погрешность 5*10^-4

Значит, в десятичной системе исчисления max погрешность 5*10^-k

Виды ошибок

- ошибки в исходной информации

- ошибки ограничения

- ошибки округления

2. Относительные и абсолютные ошибки.

3. Распространение ошибок.

Абсолютные ошибки.

Сложение

Вычитание

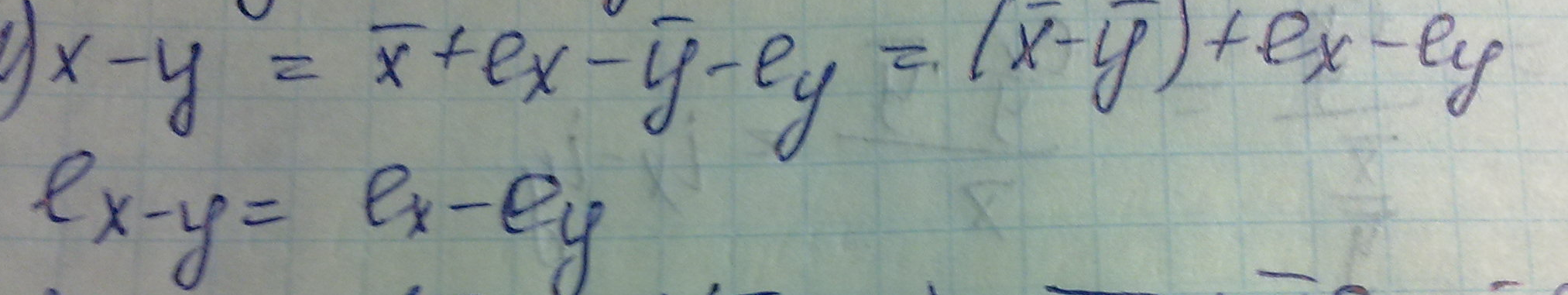
Умножение

Деление

Относительные ошибки.Сложение.

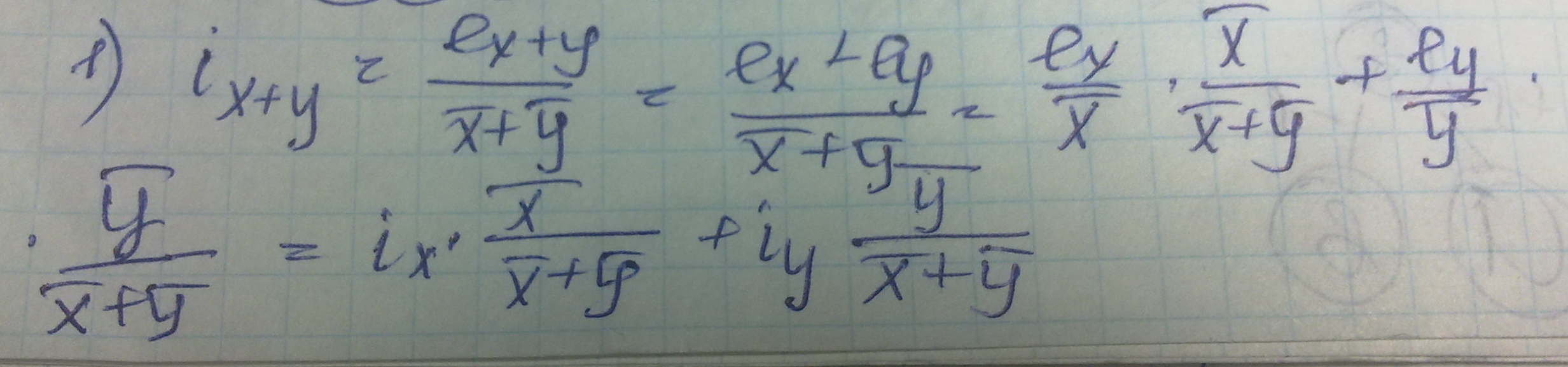
Вычитание.

Умножение

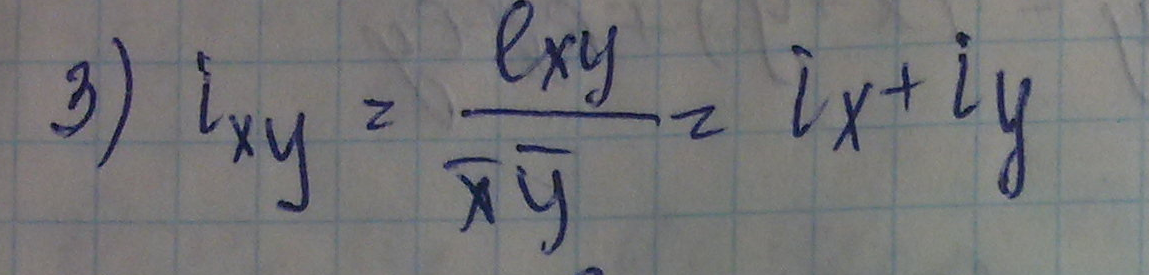
Деление

4. Графы вычислительных процессов.

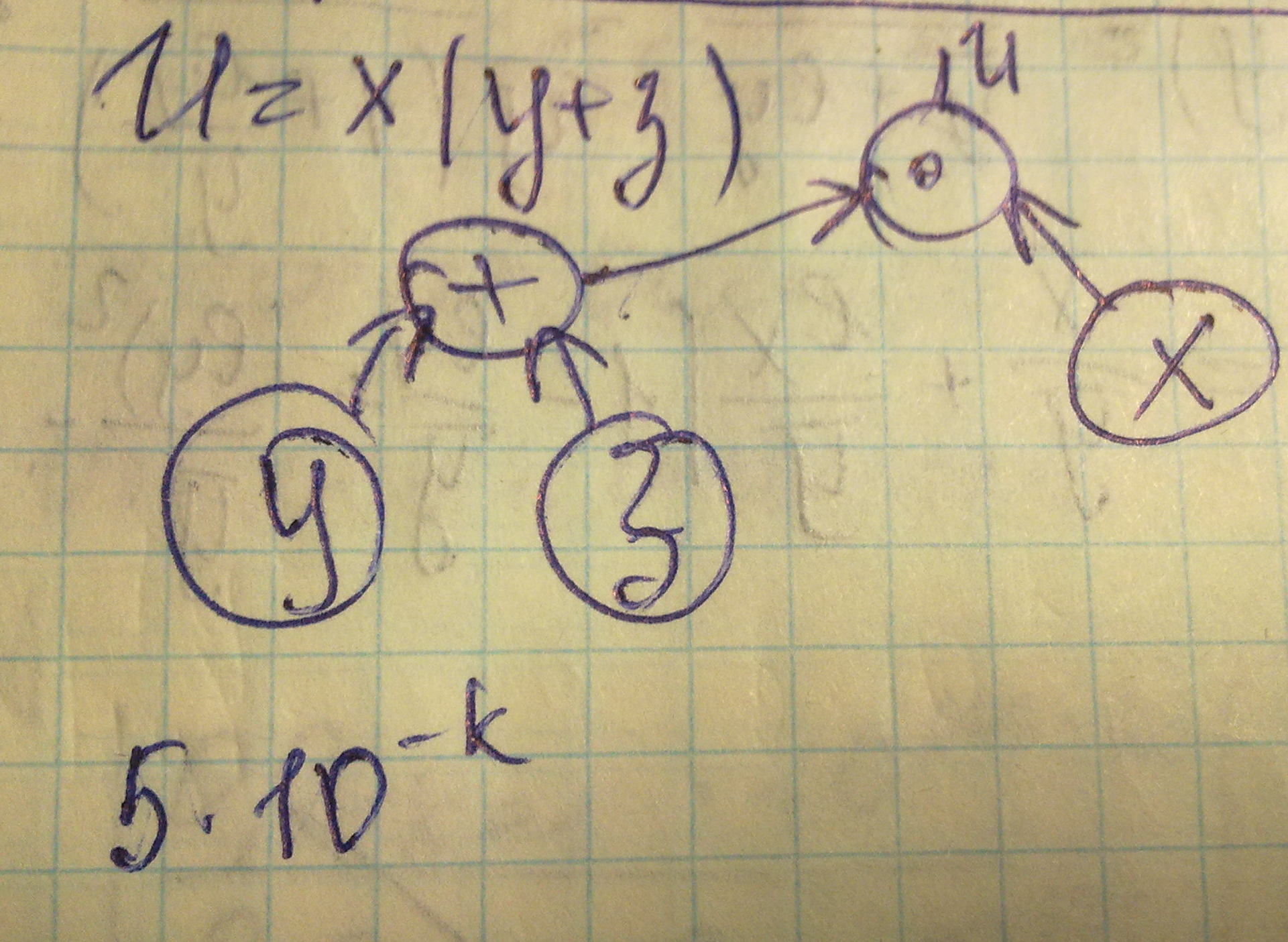
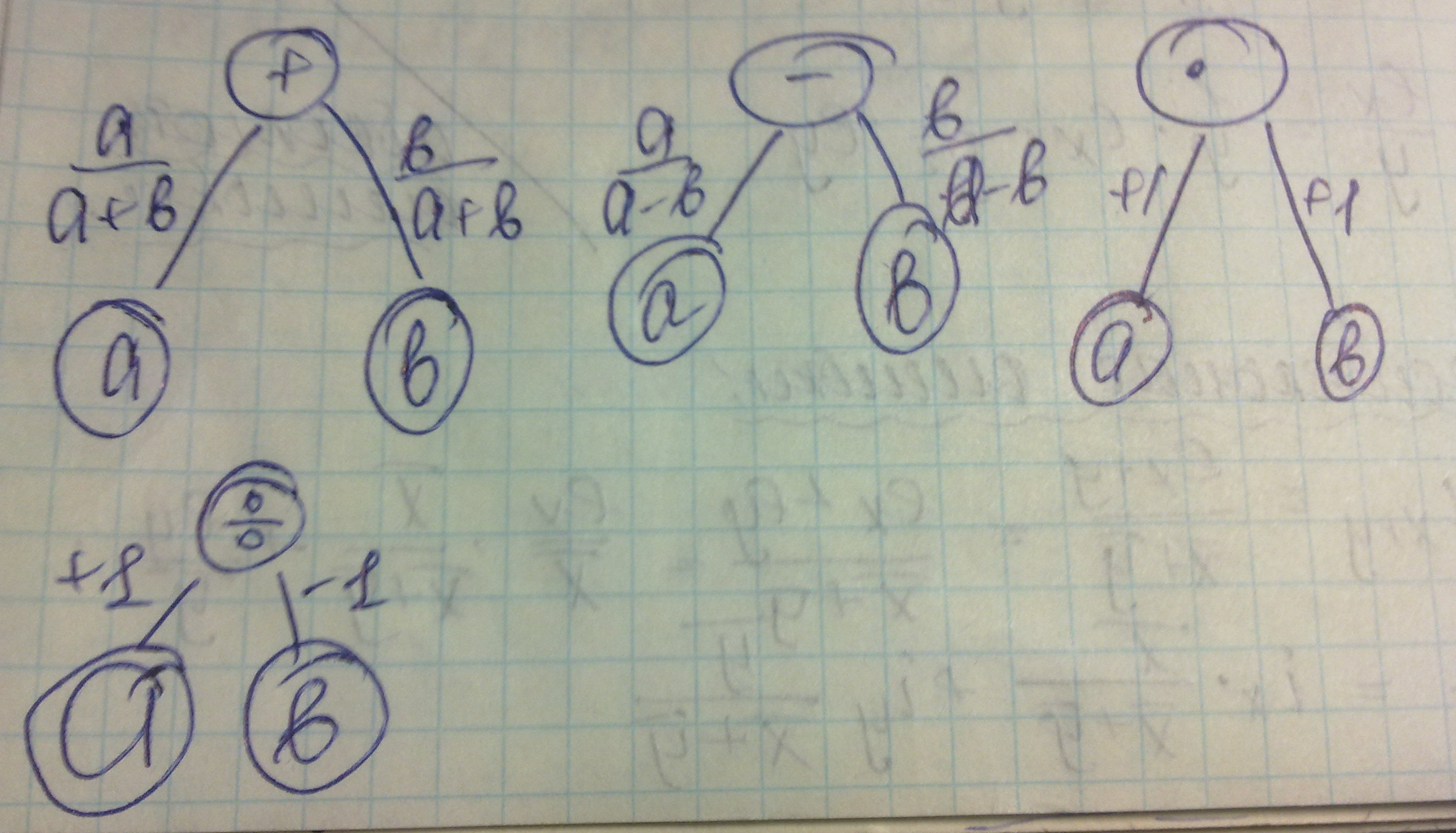
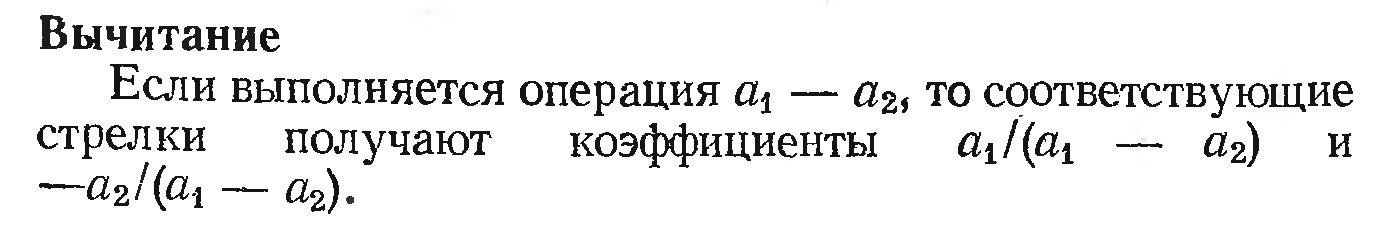
5. Степенные ряды. Ошибки.

Ряд, членами которого являются степенные функции аргумента x, называется степенным рядом.

«Математическое» определение синуса через его разложение в степенной ряд пригодно для всех значений аргумента , но при этом подразумевается , что вычисление синуса необходимо производить с бесконечно большим количеством значащих цифр.

Вспомним, что для целого n: