21. Вычисление производных.

Численное дифференцирование.

1. Аппроксимация производных.

Производной функции y=f(x) называется предел отношения приращения Δу к приращению аргумента Δх при стремлении Δх к нулю:

(1)

Это соотношение называется аппроксимацией (приближением) производной с помощью отношения конечных разностей (значения Δу, Δх – конечные).

(3.3)

(3.4)

с помощью правых разностей;

, (3.5) с помощью центральных разностей.

Таким образом, используя формулу (1), можно найти приближенные значения производных любого порядка. При этом остается открытым вопрос о точности полученных значений. Кроме того, для хорошей аппроксимации производной нужно использовать значения функции во многих узлах, а в формуле (1) это не предусмотрено.

2. Погрешность численного дифференцирования.

Аппроксимируем функцию f(x) некоторой функции ϕ(х), т.е. представим ее в виде:

(3.7)

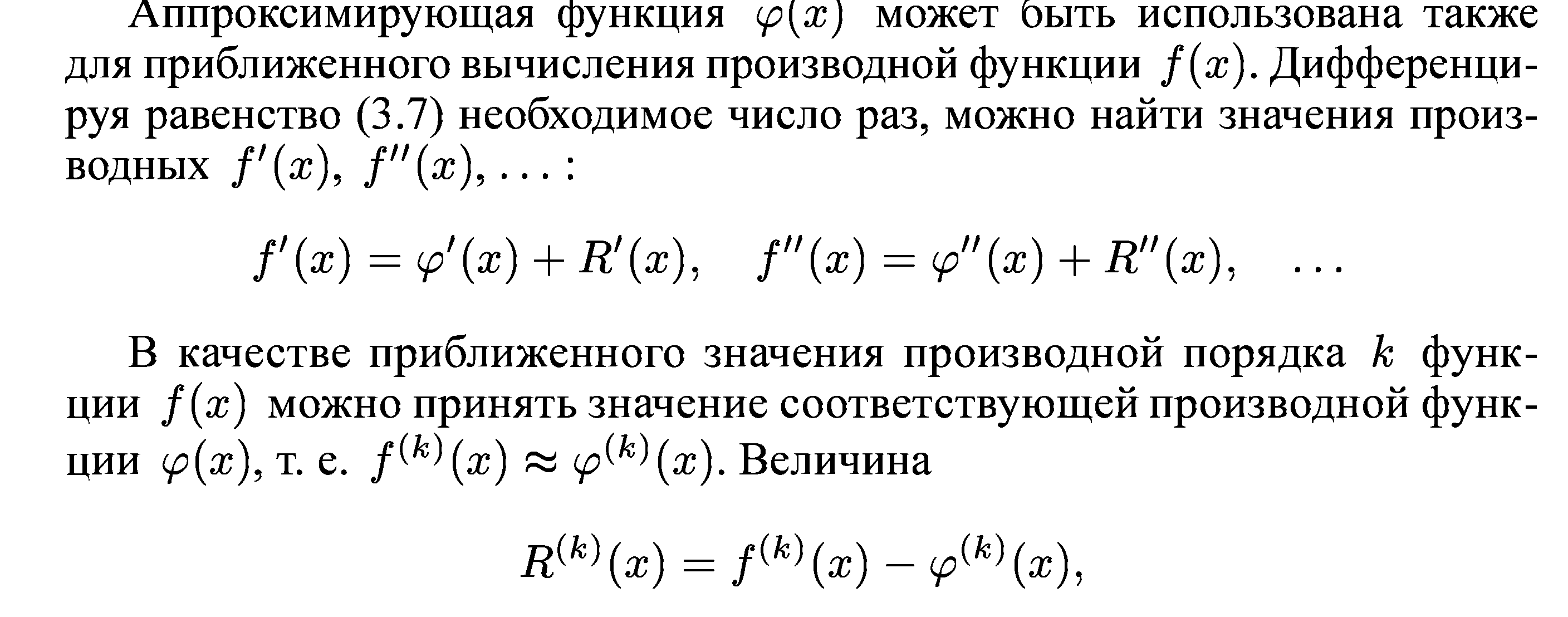
характеризующая отклонение приближенного значения производной от ее истинного значения, называется погрешностью аппроксимации производной.

порядком погрешности аппроксимации производной (или порядком точности данной аппроксимации). При этом предполагается, что значение шага по модулю меньше единицы. Оценку погрешности легко проиллюстрировать с помощью ряда Тейлора:

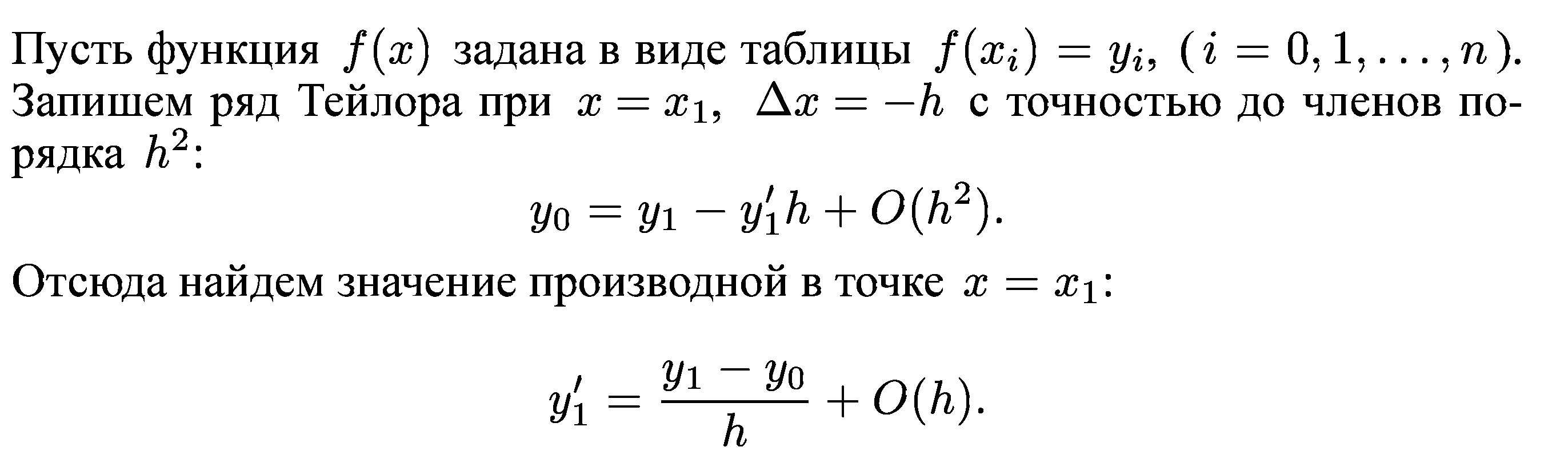
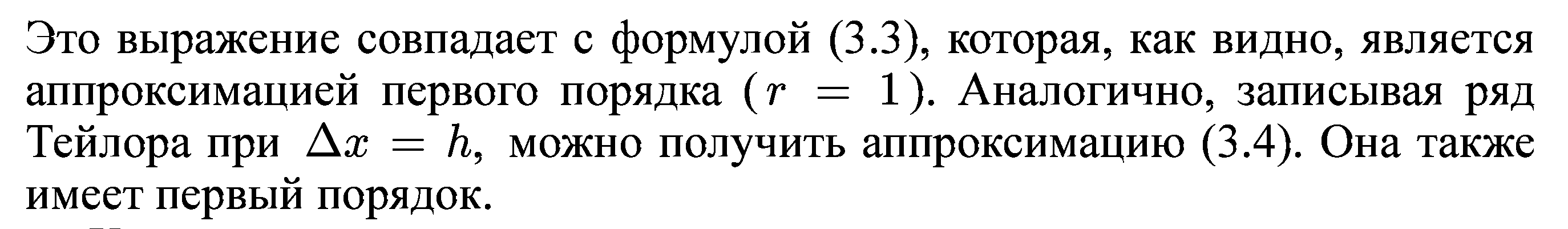
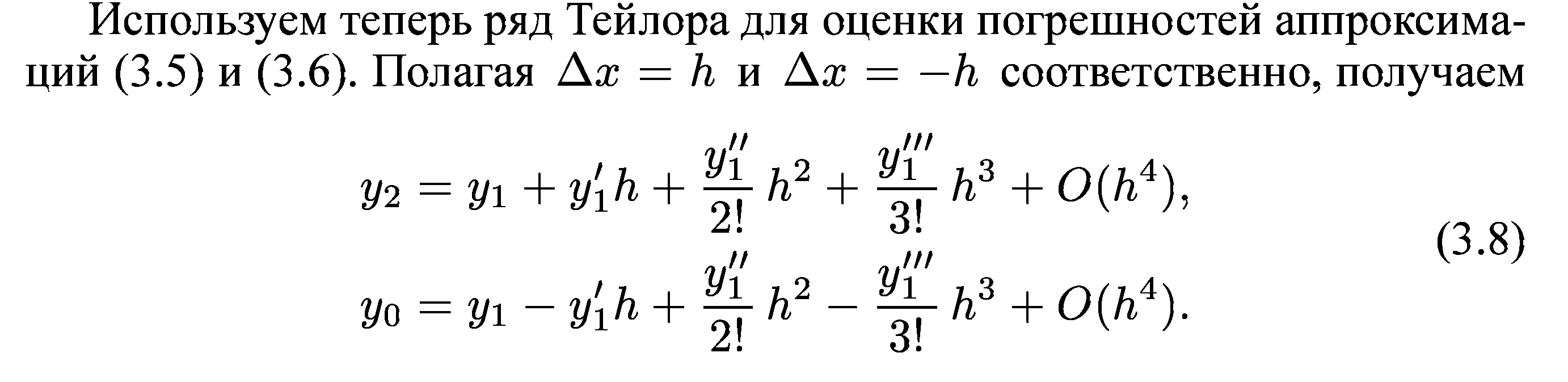
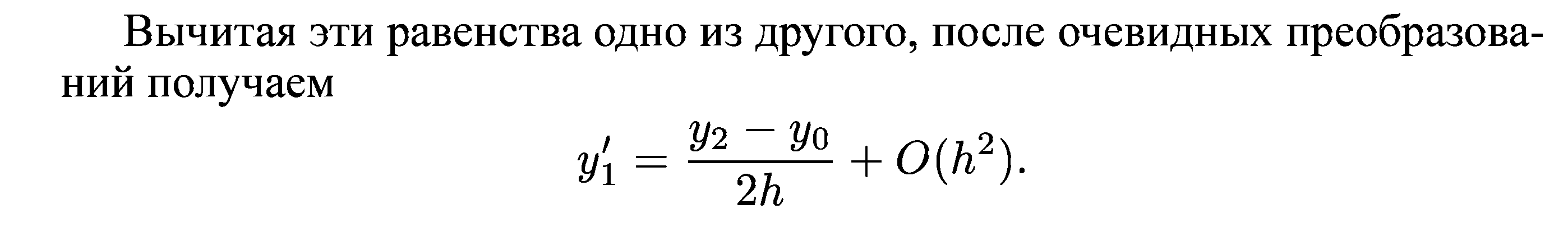
Это аппроксимация производной (3.5) с помощью центральных разностей. Она имеет второй порядок. Складывая равенства (3.8), находим оценку погрешности аппроксимации производной второго порядка вида:

Таким образом, эта аппроксимация имеет второй порядок. Аналогично можно получить аппроксимации производных более высоких порядков и оценку их погрешностей.

3. Использование интерполяционных формул.

Предположим, что функция f(x), заданная в виде таблицы с постоянным шагом h = x i– x i-1(i = 1, 2,..., n), может быть аппроксимирована интерполяционным многочленом Ньютона:

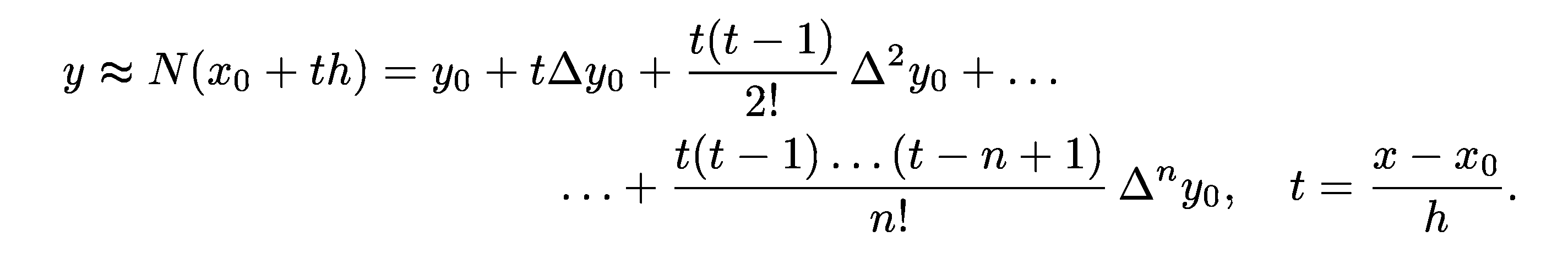
Дифференцируя этот многочлен по переменной х с учетом правила дифференцирования сложной функции:

можно получить формулы для вычисления производных любого порядка:

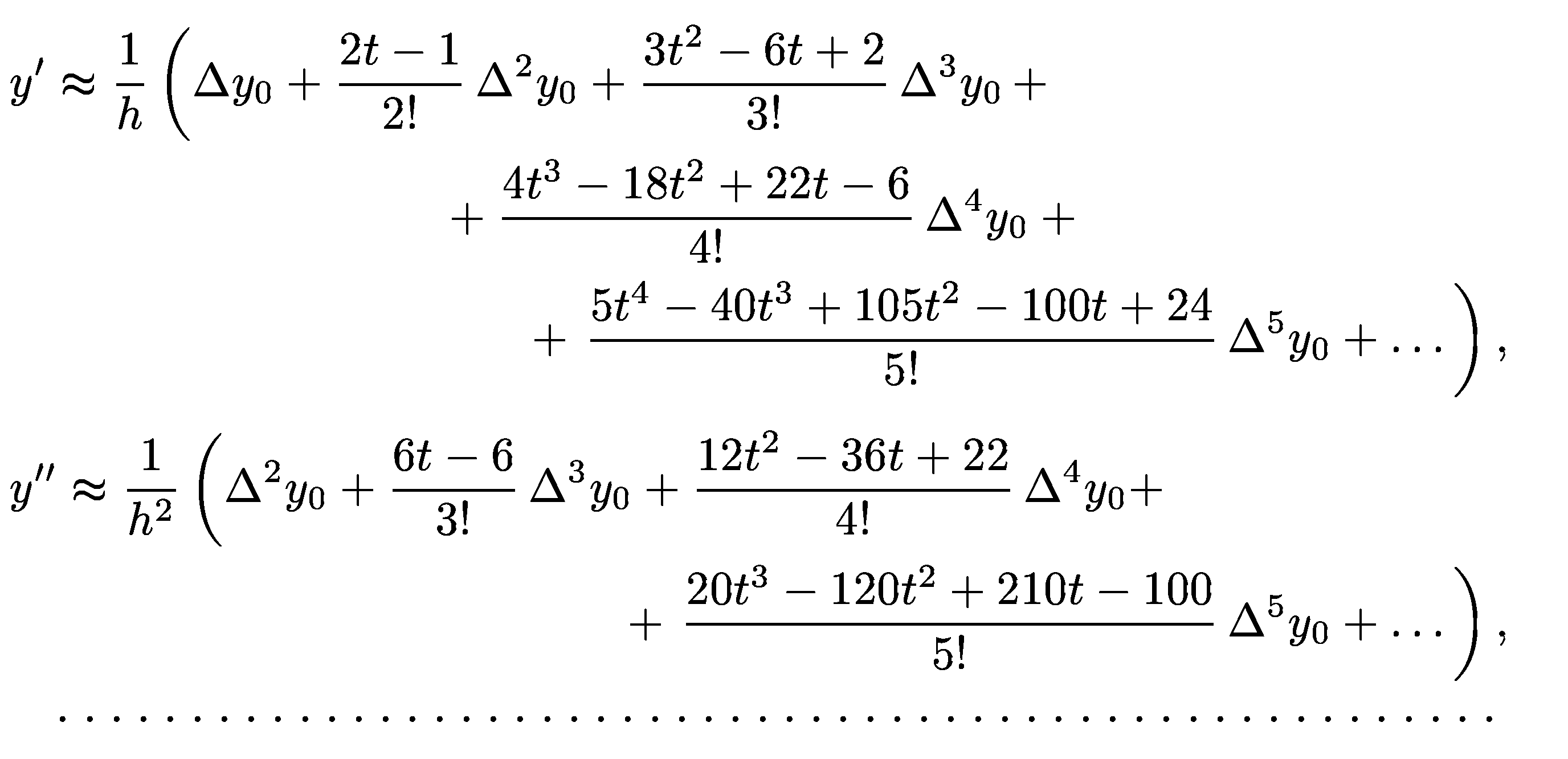
Число слагаемых в этих формулах зависит от количества узлов, используемых для вычисления производных. Как и при построении многочлена Ньютона, добавление к шаблону нового узла означает добавление к сумме одного слагаемого.

4. Метод неопределенных коэффициентов.

Искомое выражение для производной k-то порядка в некоторой точке

х = Х I представляется в виде линейной комбинации заданных значений функции в узлах x0, х1, ... , хn: (1)

Предполагается, что это соотношение выполняется точно, если функция у

является многочленом степени не выше n, т. е. может быть представлена в виде:

Отсюда следует, что соотношение (1) должно выполняться точно для многочленов у = 1, у = х - х0, ... , у = (х – х0)^n. Подставляя последовательно эти выражения в (1) и требуя выполнения точного равенства, получаем систему n+ 1 линейных алгебраических уравнений для определения неизвестных коэффициентов c0, c1, ... , сn.

22. Методы одномерной оптимизации

Под оптимизацией понимают процесс выбора наилучшего варианта из всех возможных. С точки зрения инженерных расчетов методы оптимизации позволяют выбрать наилучший вариант конструкции, наилучшее распределение ресурсов и т. п. При решении инженерных задач их принято называть проектными параметрами, а в экономических задачах их обычно называют параметрами плана. В качестве проектных параметров могут быть, в частности, значения линейных размеров объекта, массы, температуры и т. п. Число n проектных параметров x1, x2,... , хn характеризует размерность (и степень сложности) задачи оптимизации.

В процессе решения задачи оптимизации обычно необходимо найти оптимальные значения некоторых параметров, определяющих данную задачу.

Одномерная оптимизация.

1. Задачи на экстремум. Одномерная задача оптимизации в общем случае формулируется следующим образом. Найти наименьшее (или наибольшее) значение целевой функции у = f(x), заданной на множестве а, и определить значение проектного параметра х принадлежит а, при котором целевая функция принимает экстремальное значение. Существование решения поставленной задачи вытекает из следующей теоремы.

Теорема Вейерштрасса. Всякая функция f(x), непрерывная на отрезке [а, b], принимает на этом отрезке наименьшее и наибольшее значения, т. е. на отрезке [а, b] существуют такие точки х1 и х2, что для любого х принадлежащему [а, b] имеют место неравенства f(x1) < f(x) < f(x2).

Эта теорема не доказывает единственности решения. Не исключена возможность достижения равных экстремальных значений сразу в нескольких точках данного отрезка. В частности, такая ситуация имеет место для периодической функции, рассматриваемой на отрезке, содержащем несколько периодов.

Будем рассматривать методы оптимизации для разных классов целевых функций.

Пример. Найти наименьшее и наибольшее значения функции f(x) = = х^3/3 — х^2 на отрезке [1,3].

Решение. Вычислим производную этой функции:

f'(x) =x^2 -2x.

Приравнивая ее нулю, найдем критические точки:

Х^2 - 2х = 0, х1 = 0, х2 = 2.

Точка х = 0 лежит вне рассматриваемого отрезка, поэтому для анализа оставляем три точки: а = 1, х2 = 2, b = 3. Вычисляем значения функции в этих точках:

f(1) = -2/3, f(2) = -4/3, f(3)=0.

Сравнивая полученные величины, находим, что наименьшего значения функция f(x) достигает в точке х = 2, наибольшего — в точке х = 3, т. е.

fmin = f(2) = -4/3, fmax = f(3) = 0.

В рассмотренном примере уравнение f'(x) = 0 для отыскания критических точек удалось решить непосредственно. Для более сложных видов производной функции f'(x) необходимо использовать численные методы решения нелинейных уравнений.

2. Методы поиска. Численные методы поиска экстремальных значений функции рассмотрим на примере нахождения минимума функции f(x) на отрезке [а, Ь]. Будем предполагать, что целевая функция унимодальна, т. е. на данном отрезке она имеет только один минимум.

Погрешность приближенного решения задачи определяется разностью между оптимальным значением х проектного параметра и приближением к нему x*. Потребуем, чтобы эта погрешность была по модулю меньше заданного допустимого значения е:

|х — х*| < e (1)

Процесс решения задачи методом поиска состоит в последовательном сужении интервала изменения проектного параметра, называемого интервалом неопределенности. В начале процесса оптимизации его длина равна

b — а, а к концу она должна стать меньше е, т. е. оптимальное значение проектного параметра должно находиться в интервале неопределенности — отрезке [xn,xn+1], причем хn+1 — хn < е.

Для выполнения условия (1) достаточно выполнения неравенства xn+1— хn < 2е.

Наиболее простым способом сужения интервала неопределенности является деление его на некоторое число равных частей с последующим вычислением значений целевой функции в точках разбиения. Пусть n — число элементарных отрезков, h = (Ъ — а)/n — шаг разбиения. Вычислим значения целевой функции yk-ый = f(x k-ое) в узлах xk-ое = а + k*h

(к = 0,1,... ,п). Сравнивая полученные значения f(xk), найдем среди них наименьшее

Y i-ый =f(x i-ый).

Число m n-ый = y i-ый можно приближенно принять за наименьшее значение целевой функции f(x) на отрезке [а, b]. Очевидно, что близость m n-ый к минимуму m зависит от числа точек, и для непрерывной функции f(x) lim m n-ый = m, m стремится к бесконечности, т. е. с увеличением числа точек разбиения погрешность в определении минимума стремится к нулю.

В данном методе (метод перебора), основная трудность состоит в выборе n и оценке погрешности. Можно провести оптимизацию с разными шагами и исследовать сходимость такого итерационного процесса. Но это трудоемкий путь.

Более экономичным способом уточнения оптимального параметра является использование свойства унимодальности целевой функции, которое позволяет построить процесс сужения интервала неопределенности.

Пример.

Пусть начальная длина интервала неопределенности равна b — а = 1. Нужно добиться его уменьшения в 100 раз.

Сначала разобьем отрезок [а, b] на 20 частей и найдем интервал неопределенности длиной 0.1, при этом вычислим значения целевой функции в точках Хк = а + 0.05k (к = 0,1,..., 20) Теперь отрезок [x i-1, x i+1] снова разобьем на 20 частей; получим искомый интервал длиной 0.01, причем значения целевой функции вычисляем в точках Хк = Xi-1+ 0.005k (к = 1,2,..., 19). Это наиболее экономичный способ.