
Вопросы 11-15 (без 14-го, т е без :Метод Гаусса. Сравнение методов численного интегрирования.)
11) Полиномиальная интерполяция
Интерполя́ция, интерполи́рование — в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений.
. Задача построения функции на основании некоторых наборов значений называется аппроксимацией. Интерполяцией называют такую разновидность аппроксимации, при которой кривая построенной функции проходит точно через имеющиеся точки данных.
Существует также близкая к интерполяции задача, которая заключается в аппроксимации какой-либо сложной функции другой, более простой функцией. Если некоторая функция слишком сложна для производительных вычислений, можно попытаться вычислить её значение в нескольких точках, а по ним построить, то есть интерполировать, более простую функцию. В некоторых классах задач достигнутый выигрыш в простоте и скорости вычислений может перевесить получаемую погрешность в результатах.
Рассмотрим
систему несовпадающих точек ![]() (
(![]() )
из некоторой области
)
из некоторой области ![]() .
Пусть значения функции
.
Пусть значения функции ![]() известны
только в этих точках:
известны
только в этих точках:
![]()
Задача
интерполяции состоит в поиске такой
функции ![]() из
заданного класса функций, что
из
заданного класса функций, что
![]()
-
Точки
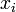 называют узлами
интерполяции,
а их совокупность — интерполяционной
сеткой.
называют узлами
интерполяции,
а их совокупность — интерполяционной
сеткой. -
Пары
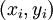 называют точками
данных или базовыми
точками.
называют точками
данных или базовыми
точками. -
Разность между «соседними» значениями
 — шагом
интерполяционной сетки.
Он может быть как переменным, так и
постоянным.
— шагом
интерполяционной сетки.
Он может быть как переменным, так и
постоянным. -
Функцию
 — интерполирующей
функцией или интерполянтом.
— интерполирующей
функцией или интерполянтом.
В нашем курсе мы рассмотрели 2 способа полиномиальной интерполяции – через полином Лагранжа и через метод сплайнов.
Интерполяцио́нный
многочле́н Лагра́нжа — многочлен минимальной
степени, принимающий данные значения
в данном наборе точек. Для ![]() пар
чисел
пар
чисел ![]() ,
где все
,
где все ![]() различны,
существует единственный многочлен
различны,
существует единственный многочлен ![]() степени
не более
степени
не более ![]() ,
для которого
,
для которого ![]() .
.
В
простейшем случае (![]() )
— это линейный многочлен, график которого
— прямая, проходящая через две заданные
точки.
)
— это линейный многочлен, график которого
— прямая, проходящая через две заданные
точки.
Лагранж предложил способ вычисления таких многочленов:
![]()
где базисные полиномы определяются по формуле:

![]() обладают
следующими свойствами:
обладают
следующими свойствами:
-
являются многочленами степени
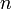
-
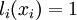
-
 при
при 
Отсюда
следует, что ![]() ,
как линейная
комбинация
,
как линейная
комбинация ![]() ,
может иметь степень не больше
,
может иметь степень не больше ![]() ,
и
,
и ![]() ,
,
Погрешность
K(x)=j(x)-Ln(x)
|
j(x)
- Ln(x)
|≤

M(n+1) = max [x0…xn] | f (n+1) (x)|
x i+1-xi=h
Метод Лагранжа применяется, если не много точек. Иначе выбирают некоторый промежуток в окрестности искомого значения и вычисляют, а затем склеивают. В результате получается ломаная, и в точках соединения не будет производной. Это называется методом сплайнов.
Сплайн – это некий стержень, концы которого закреплены с некоторой погрешностью.
Можно потребовать, чтобы функция склеивалась не только по значениям, но и по I и II производным. Далее мы выведем формулы. Ими будет задаваться условие совпадения в точках склеивания значений функций, а также I и II производных. Или же, что мне не до конца ясно, мы будем находить коэффициенты ai+1 bi+1 ci+1 di+1 для функции нового отрезка. В общем, вот:
Кубический сплайн – полином третьей степени:
y = ai (x-xi)3 + bi (x-xi) 2 + ci(x-xi)+di
x принадлежит [ xi, xi+1], i=0….n-1.
Будем считать, что сетка равномерная, т е x i+1=xi+h
Задаем первое условие: совпадение значений функций -
В этой точке значения левого и правого отрезка должны совпасть:
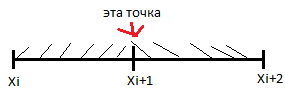
x=xi
yi=di
x=xi+1 i=0….n-1
yi+1 = ai h3 +bi h2 +ci h+ di
Добиваемся равенства первых производных на концах отрезка:
y1’=3 ai (x-xi)2 + 2 bi(x-xi) + ci
x=xi+1
y1’=3 ai h2+ 2 bi h + ci
y2=a i+1 (x-x i+1)3 +b i+1 (x-x i+1)2 +c i+1 (x-x i+1) + d i+1
y2’=3 a i+1 (x-x i+1)2 +2 b i+1 (x-x i+1) +c i+1
y’ (x i+1) = c i+1
Здесь мы приравниваем y1’ и y’ (x i+1):
3 ai h2+ 2 bi h + ci = c i+1 ; i=0…n-2
(отсюда можно найти = c i+1 )
Добиваемся равенства вторых производных:
y1’’=6 ai h+ 2 bi
y2’’=6 a i+1 (x-x i+1) +2 b i+1
y2’’ (x i+1)= 2 b i+1
6 ai h+ 2 bi = 2 b i+1
отсюда можно найти b i+1.
Найдя коэффициенты b i+1 c i+1 di , мы можем найти a i+1. (В лекции это не рассматривалось)

i=0….n-2
Естественным кубическим сплайном называется кубический сплайн, удовлетворяющий также граничным условиям вида:
y’’(x0)=0
y’’(xn)=0
Вывод: на выходе мы получаем вместо многочлена n-ной степени некоторое количество кубических многочленов, что может дать некоторое упрощение вычислений. Кроме того, достигается более плавная стыковка функций.
12) Численное интегрирование. Метод трапеций
Интеграл функции — аналог суммы последовательности. Неформально говоря, (определённый) интеграл является площадью части графика функции (в пределах интегрирования), то есть площадью криволинейной трапеции. Определенным интегралом от функции f(x) на отрезке [а, b] называется предел интегральной суммы при таком неограниченном увеличении числа точек разбиения, при котором длина наибольшего из элементарных отрезков стремится к нулю:

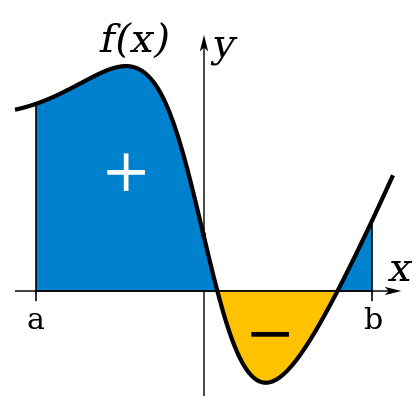
I=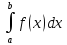 где a,b
– конечны, f(x)
– непрерывна на отрезке от a
до b,
т е [a,b]
где a,b
– конечны, f(x)
– непрерывна на отрезке от a
до b,
т е [a,b]
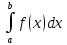 =
F(b)-F(a)
– это формула Ньютона-Лейбница, здесь
F(x)
– первообразная в данной точке.
=
F(b)-F(a)
– это формула Ньютона-Лейбница, здесь
F(x)
– первообразная в данной точке.
Численное интегрирование — вычисление значения определённого интеграла (как правило, приближённое). Под численным интегрированием понимают набор численных методов отыскания значения определённого интеграла.
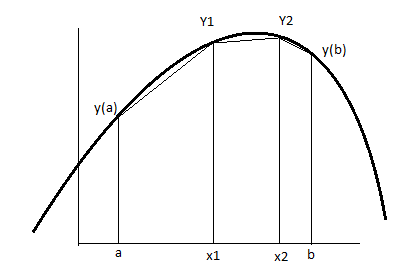
Метод трапеций: Основная идея метода трапеций в том, что мы заменяем исходный график ломаной линией, соединяющей точки (xi, yi). На данном рисунке мы разбиваем отрезок на три части.
и вместо кривой на каждом отрезке берем прямую, соединяющую конца отрезка xi xi+1:
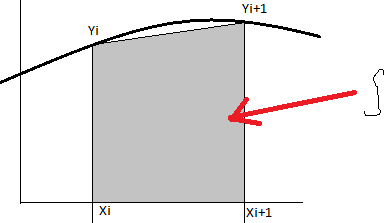
Ii
=

Считаем, что разбиение с равным шагом, т е xi+1 – xi=h
Тогда Ii = Sтрап – находим площадь трапеции Yi Yi+1 Xi+1 Xi: это полусумма оснований, умноженная на высоту. Высота будет Xi+1-Xi=h; Основания это Yi и Yi+1, итого получаем:
Ii = ½ h (yi+yi+1)
Тогда
весь интеграл I=
и это будет равно h/2 (y0 +2 y1 + 2 y2 + ….+ 2yn-2 +2 yn-1+ yn). Двойки появились потому, что все yi , кроме граничных, повторяются дважды.
Найдем погрешность этой формулы. (Мы берем функцию x2 )
Ошибка ограничения:
 =
1/3 (
=
1/3 (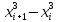 )
= 1/3 (
)
= 1/3 (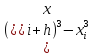 )
= 1/3(
)
= 1/3( )
=
)
=
а)

Ii
= h/2
(yi
+ yi+1)
+ E=
h/2(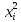 +
+
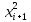 )
+ E
= h/2(
)
+ E
= h/2( +
+
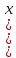 )2
)+ E
= h/2(
)2
)+ E
= h/2(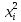 +
+ + 2 xi*h
+ h2)+
E
= h/2(
+ 2 xi*h
+ h2)+
E
= h/2(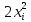 + 2 xi*h
+ h2)+
E
=
+ 2 xi*h
+ h2)+
E
=
б)
h
 + xi*h2
+ h3/2+
Ei
+ xi*h2
+ h3/2+
Ei
Как видно, в а) и б) получились похожие выражения. Выразим оттуда Еi:
Ei
=
 = - 1/6 h3
= - 1/6 h3
ETi = -1/6 h3
Тогда найдем k: (k – это некоторая константа, коэффициент ошибки или нечто в этом роде)
Ei = k h2 (2 xi+1 – 2 xi)= 2kh3
-1/6 h3= 2kh3
k = -1/12
отсюда
Ошибка округления
e= - h2 /12 (b - a) y’’(ξ) a ≤ ξ ≤ b
|e|≤ h2 /12 (b - a) M , где M=max(| y’’|)
Формула экстраполяционного перехода к пределу:
Ih = h/2 (y0 +2 y1 + 2 y2 + ….+ 2yn-2 +2 yn-1+ yn). h= (b-a)/n
Пусть I=Ih + c h2 ; с= (b-a)/12 * y’’(ξ) a ≤ ξ ≤ b.
Пусть y’’(ξ) = const, тогда с = const
Возьмем приближенное значение I с шагом k; k = (b-a)/m
I = Ik + ck2 ;
c = (I - Ih) / h2
Продолжая
выводить эту формулу, получаем, I
= (Ik
-
Ih
 )
/ (1 -
)
/ (1 -
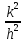 )
)
Такж
эту формулу можно переписать в другом
виде: I
= Ih
+

При шаге k = 2h формула примет следующий вид:
I = 4/3 Ih – 1/3 Ik
13) Метод Симпсона. Сравнение методов численного интегрирования.
Разобьем отрезок интегрирования [а, b] на четное число п равных частей с шагом h. Па каждом отрезке [x0, х2], [x2, x4], …, [xi-1,xi+1],...... , [хn-2,хn] подынтегральную функцию f(x) заменим интерполяционным многочленом второй степени:
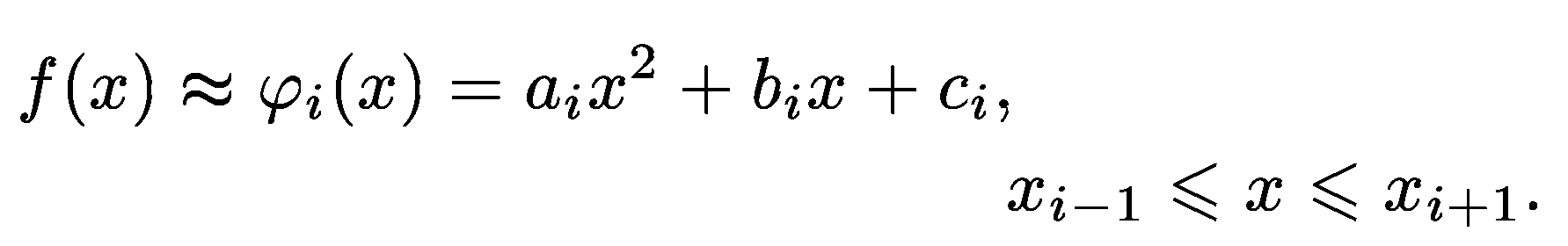
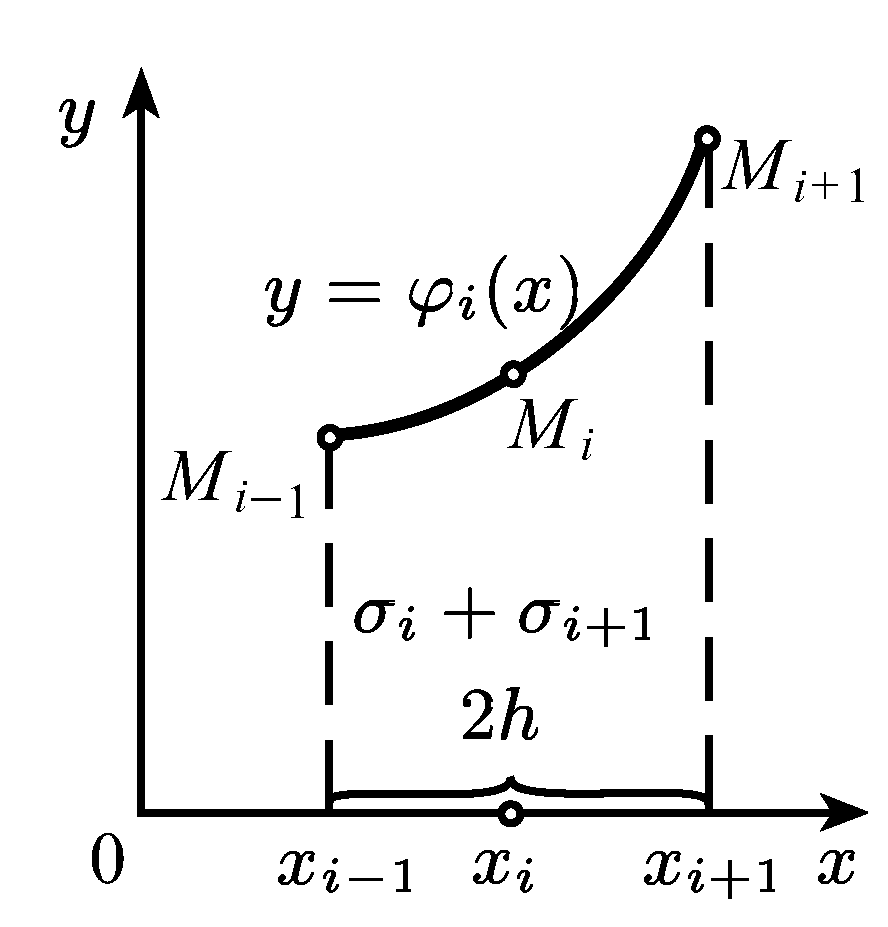
Иными словами, суть метода Симпсона в том, что мы вместо исходной плохо интегрируемой кривой берем отрезки квадратичной функции, и потом находим сумму интегралов под ней.

Формулу Симпсона можно вывести, применив экстраполяционный переход к пределу к формуле из метода трапеций:
Ih = h/2 (y0 +2 y1+ 2 y2 + ….+ 2 yn-2 +2 yn-1+ yn).
Возьмем шаг k= 2 h:
Ik = h (y0 + 2 y2 + ….+ 2 yn-2 + yn).
Согласно формуле, I=4/3 Ih – 1/3 Ik
Т е
I = 2 h/3 (y0 +2 y1+ 2 y2 + ….+ 2 yn-2 +2 yn-1+ yn) - h/3 (y0 + 2 y2 + ….+ 2 yn-2 + yn) =
h/3 (2 y0 +4 y1+ 4 y2 + ….+ 4 yn-2 +4 yn-1+ 2 yn) - h/3 (y0 + 2 y2 + ….+ 2 yn-2 + yn) =
h/3 (2 y0 - y0 +4 y1+ 4 y2 - 2 y2+ ….+ 4 yn-2 - 2 yn-2 +4 yn-1+ 2 yn - yn) =
h/3 ( y0 +4 y1+ 2 y2 + ….+ 2 yn-2 +4 yn-1+ yn)
Ошибка ограничения: (опять же для формулы y=x2)
e ≈ h^4 /180 (b-a) f(IV) (ξ); a ≤ ξ ≤ b
Ошибка округления 1/h
Далее мы рассматриваем в общем виде нечто, из чего сначала выводим формулу для метода трапеций, затем для метода Симпсона, затем утверждаем, что произвольный полином можно представить в таком же виде, как это нечто, разложив его в ряд Тейлора. Из этого мы делаем вывод, что формула Симпсона точна даже для полиномов третьей степени.
Кроме того, как выяснилось, формула экстраполяционного перехода к пределу у метода Симпсона отличается, и выглядит следующим образом:
Раз формула точна для полиномов третьей степени, значит ошибка будет порядка 4й степени, поэтому мы берем следующие выражения:
I = Ih + c h4 ; I = Ik + c k4 откуда получаем:
I
=
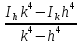
При k = 2h формула принимает следующий вид:
I = 1/15 (16 Ih - Ik)
Сравнительная характеристика методов:
метод трапеций – просто считать
метод Симпсона – меньше слагаемых для той же точности, относительно несложен.
Для итерационного процесса подходят оба эти метода, т. к при повышении точности пошагово нужно меньше вычислений. В методе Гаусса (метод Гаусса для вычисления интегралов, см подробнее МкКракен с. 219) подобной экономии вычислений не происходит.
Кроме того, при использовании любого итерационного метода ошибка не накапливается, так как предыдущий полученный результат можно принять за начальный.
15) Системы линейных алгебраических уравнений. Итерационные методы.
Система линейных уравнений имеет единственное решение, если прямые, соответствующие линейным уравнениям, пересекаются.
Также система может не иметь решений (если прямые параллельны), или иметь бесчисленное множество решений (если прямые совпадают) (также вырожденное или почти вырожденное)
С точки зрения определителей в матрицах коэффициентов то же самое можно выразить так:
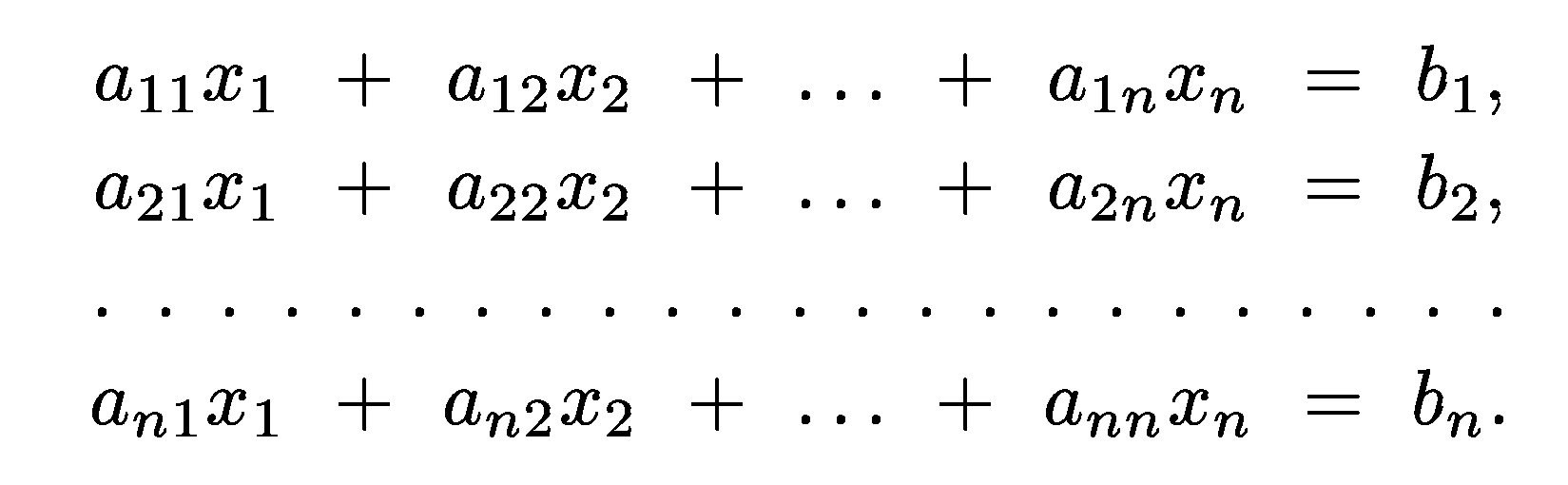 -
система уравнений
-
система уравнений
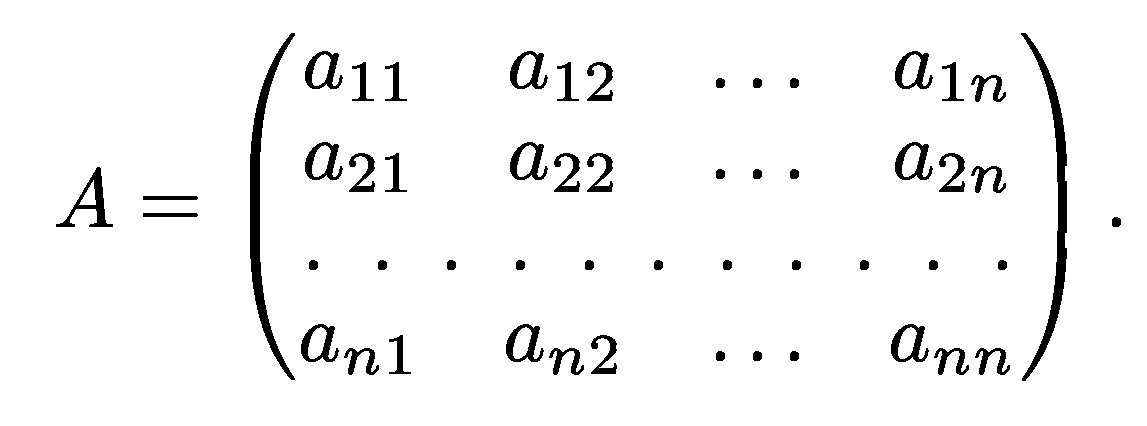 -
матрица коэффициентов
-
матрица коэффициентов
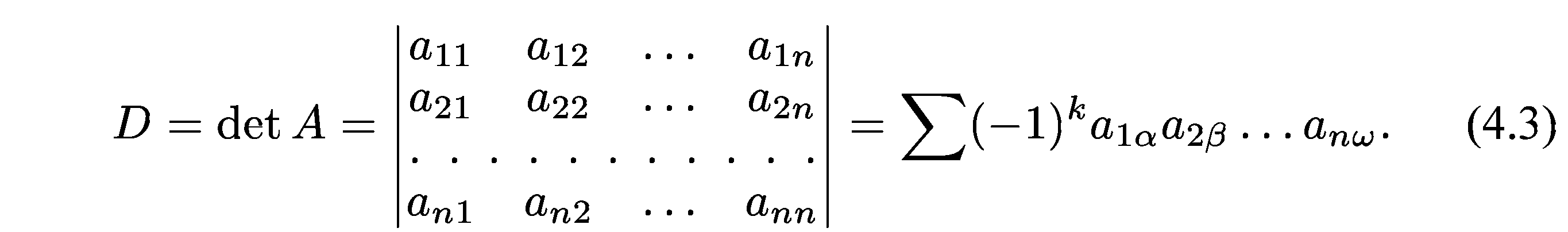
Здесь индексы а, β, ... , ω пробегают все возможные n! перестановок
номеров 1,2,... , n! k — число инверсий в данной перестановке (Под инверсией понимается обмен двух индексов местами; с помощью таких обменов перестановка а, β, ... , ω получается из перестановки 1, 2, ... , n)
Необходимым и достаточным условием существования единственного решения системы линейных уравнений является условие D ≠ 0. В случае равенства нулю определителя системы матрица называется вырожденной; при этом система линейных уравнений либо не имеет решения, либо имеет их бесконечное множество.
Рассмотрим три возможных случая взаимного расположения двух прямых на плоскости:
![]() -
две
прямые
-
две
прямые
-
прямые пересекаются, т. е. коэффициенты системы не пропорциональны:
![]()
2) прямые параллельны , т. е. коэффициенты системы подчиняются условиям
![]() 3) прямые
совпадают, т. е. все коэффициенты
пропорциональны:
3) прямые
совпадают, т. е. все коэффициенты
пропорциональны:
![]()
Также существует случай почти вырожденной системы, пример
5 x+ 7y = 12.
7 x + 10y=17. (12. ; 7. округленные числа)
решениями будут х =1 ; у=1 Или х = 2.415 ; у=0
Формально решение должно быть единственным. Это называется плохо обусловленной системой и на практике встречается довольно часто. Графически выглядит так:

Метод исключения Гаусса:
 Пусть
у нас такая система. Надо привести
матрицу коэффициентов левой части к
треугольному виду, т е чтобы все элементы,
стоящие под главной диагональю, были
нулями. (После этого выразить х будет
делом техники.)
Пусть
у нас такая система. Надо привести
матрицу коэффициентов левой части к
треугольному виду, т е чтобы все элементы,
стоящие под главной диагональю, были
нулями. (После этого выразить х будет
делом техники.)
Чтобы получить треугольный вид, берем первое уравнение, и прибавляем его ко второму, предварительно домножив на – a21 / a11. Таким образом, во втором уравнении пропадает a21. То же самое повторяем для всех остальных уравнений системы, в нашем случае для 3его – прибавляем к нему первое уравнение, умноженное на – a31 / a11.
Продолжаем процесс для второго уравнения, теперь берем коэффициент при х2 и т д
Проблема заключается в том, что если один или несколько коэффициентов системы значительно превосходят остальные, то при домножении на них мы получаем очень большую ошибку. Для того, чтобы предотвратить подобную неприятность, используется метод Гаусса с выбранным коэффициентом. Суть его в том, что самый большой коэффициент должен по возможности попадать в знаменатель.
Метод Гаусса требует порядка n3 операций для n –мерной системы.
Уточнение решений.(это уже итерационный метод)
Пусть х0 – приближенное решение
A(x0) = b0 – приближенное к b.
A(x) - A(x0) = b - b0
A(x - x0) = b - b0
x - x0 = ξ0 ; b - b0 = β0
A ξ0 = β0
Отсюда надо найти ξ0
x0 + ξ0 = x1 – так мы получили новое приближение. так можно продолжать до тех пор, пока ξi не станет достаточно малым.
