Vychislitelnaya_matematika / Vychislitelnaya_matematika / Вычислительная математика / 16-19

16 Системы линейных алгебраических уравнений. Итерационные методы

Система из n линейных уравнений с n неизвестными выглядит так:

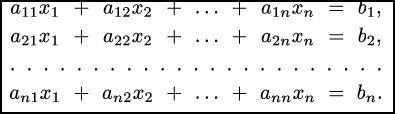
Методы решения таких систем делятся на конечные и итерационные. Итерационные методы – это методы последовательных приближений. Сначала задается некоторое приближенное решение – начальное приближение. Потом с помощью некоторого алгоритма проводится один цикл вычислений – итерация. Итерации повторяются, пока не достигается требуемая точность. Итерационный метод называется сходящимся, если с увеличением числа итераций приближенное решение стремится к точному. Погрешности окончательных результатов при использовании итерационных методов не накапливаются, поскольку точность для каждой итерации определяется только результатами предыдущей итерации и почти не зависит от вычислений, выполненных ранее.

ИТЕРАЦИОННЫЕ МЕТОДЫ:

I Уточнение решения

Этот метод используется для уточнения решения, полученного с помощью прямого метода (например, метода Гаусса). Обозначения:

Ax=b - система линейных уравнений. (Здесь Ах – матрица, а b – вектор)

x^{(0) –} начальное приближение (это вектор, то есть x⁽⁰⁾ состоит из x₁⁽⁰⁾, x₂⁽⁰⁾, …)

b⁽⁰⁾ = A x⁽⁰⁾ (то есть результат подстановки в систему начального приближения)

Δ x⁽⁰⁾ = х - x⁽⁰⁾ - погрешность полученного решения

r⁽⁰⁾ = A x⁽⁰⁾ – b = b⁽⁰⁾ – b (r называется невязкой)

Можно получить следующее равенство: А Δ x⁽⁰⁾ = - r⁽⁰⁾. Отсюда мы находим Δ x⁽⁰⁾ = - r⁽⁰⁾/A.

Первая итерация происходит следующим образом:

x⁽¹⁾=x⁽⁰⁾+ Δ x⁽⁰⁾

Общая формула имеет вид:

x^(k)=x^(k-1)+ Δ x^(k-1) ( Δ вычисляется на каждом шаге Δ x^(k) = - r^(k)/A)

Итерации продолжаются, пока не будет достигнута необходимая точность. Есть два способа это контролировать: можно брать Δ x^(k) (разность между решением на шаге k и на шаге k+1), а можно брать r^(k) (конечно, нужно отдельно считать разность для каждого элемента вектора, брать максимальный результат и сравнивать его с заданным ε).

Этот метод не рассчитан на то, что итерация может не сходиться.

II Метод простой итерации

Запишем исходную систему в стандартном виде и выполним ряд преобразований:

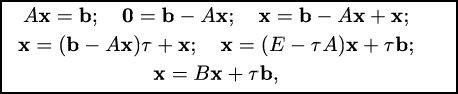
где τ – некоторое число, не равное 0, Е – единичная матрица, В=Е- τА. Получившаяся система эквивалентна исходной и служит основой для построения метода итерации. Выберем некоторое начальное приближение x⁽⁰⁾. Общая формула итерации имеет вид: x^(k)=Вх^(k-1)+ τb. От выбора параметра τ зависит сходимость метода и скорость сходимости. Справедлива теорема: Пусть у системы есть единственное решение. Метод простой итерации сходится тогда и только тогда, когда все собственные числа матрицы В = А - τЕ по модулю меньше единицы. Про собственные числа:

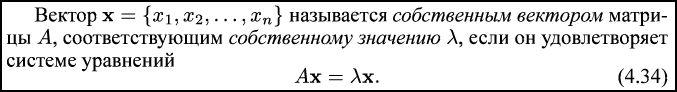
Но, надеюсь, это не надо…

II Метод Гаусса-Зейделя

Для работы этого метода необходимо добиться того, чтобы диагональные элементы не были нулевыми. Рассмотрим систему из трех уравнений (принцип алгоритма не зависит от количества уравнений):

Выразим неизвестные х₁, х₂, х₃ соответственно из первого, второго и третьего уравнений:

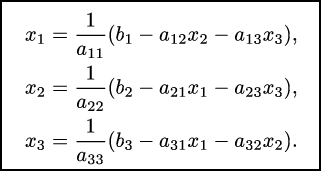
Зададим начальные приближения: x₁⁽⁰⁾, x₂⁽⁰⁾, x₃⁽⁰⁾. Будем подставлять их в уравнения и получим:

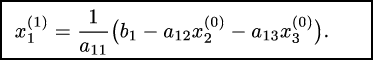
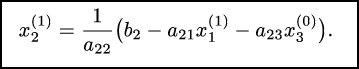(Здесь для х₁ мы подставляем уже не нулевое приближение, а только что вычисленное первое!)

Это первая итерация. Общая формула:

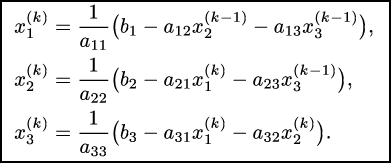
Процесс продолжается, пока разность между приближением k и k+1 не станет достаточно малой (для каждого х_j).

В общем случае (для n уравнений) алгоритм такой же: каждая переменная выражается из одного уравнения, потом в эти уравнения подставляются приближенные решения, на каждом шаге приближение становится точнее.

Для сходимости итерационного процесса достаточно, чтобы модули диагональных коэффициентов для каждого уравнения системы были не меньше сумм модулей остальных коэффициентов. При этом хотя бы одно неравенство должно выполняться строго.

(Это условие достаточное, но не необходимое)

17 Обыкновенные дифференциальные уравнения. Метод Эйлера

n – порядок дифференциального уравнения.

Задача Коши: Требуется найти функцию Y = Y(x), удовлетворяющую уравнению Y’=f(x,Y) и принимающую при x=x₀ заданное значение Y₀: Y(x₀)=Y₀. Для определенности будем считать, что значение нужно получить для x>x₀. Согласно теореме Коши решение существует, единственно и является гладкой функцией, если f(x,Y) соответствует некоторым условиям гладкости.

Теорема Коши на всякий случай:

Простейшим численным методом для решения задачи Коши является метод Эйлера. Возьмем уравнение Y’=f(x,Y). Рассмотрим его в окрестностях узлов х = х_i (i =0, 1, ….) и заменим в левой части производную на правую разность. (Это аппроксимация производной, вытекающая из определения производной как предела отношения приращения функции к приращению аргумента) Получим:

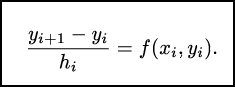
Полученная аппроксимация имеет первый порядок, т.к. при замене допускается погрешность О(h_i).

Будем считать все узлы равноотстоящими, т.е. h = const. Получим формулу:

y_i+1 = y_i + h*f(x_i, y_i) – это и есть общая формула для метода Эйлера. На первом шаге мы получим: y₁ = y₀ + h*f(x₀, y₀).

y₀ мы возьмем из заданного начального условия Y(x₀)=Y₀= y₀.

Вот общая схема работы метода Эйлера:

Геометрическая интерпретация:

Дальше начинается жесть с подсчетом ошибки. Надеюсь, это не надо, но, на всякий случай, скопирую в неизмененном виде:

18 Исправленный метод Эйлера (метод Эйлера с пересчетом)

Будем рассматривать точки, лежащие на серединах тех отрезков, которые мы рассматривали в методе Эйлера. Из формулы Y’=f(x,Y) получим:

Здесь в правой части написано среднее арифметическое значений в соседних узлах, т.о. мы получаем значение посередине.

В полученной формуле y_i+1 стоит и в левой, и в правой частях, поэтому напрямую использовать ее не удастся. Если имеется хорошее начальное приближение y_i, то построить решение можно с помощью двух итераций. Вычислим первое приближение y*_i+1 по формуле метода Эйлера: y*_i+1 = y_i + h*f(x_i, y_i). Вычисленное y*_i+1 подставим в правую часть формулы: y_i+1 = y_i + h/2[f(x_i, y_i) + f(x_i+1, y*_i+1)]. Можно записать в виде одного соотношения:

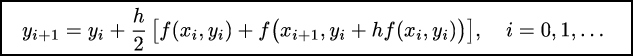
Геометрическая интерпретация:

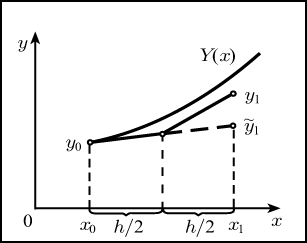
Полученный метод точнее обычного метода Эйлера. Он является методом второго порядка.

19 Модифицированный метод Эйлера (усовершенствованный метод Эйлера)

Отличается от исправленного метода Эйлера только тем, что в правой части уравнения Y’=f(x,Y) мы не берем среднее арифметическое, а пишем напрямую x+h/2. Получается

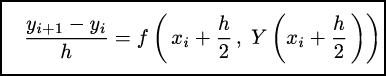
Остальное точно так же:

y*_i+1 = y_i + h*f(x_i, y_i)

Подставим y*_i+1 вместо Y(x_i+h/2):

y_i+1 = y_i + h*f(x_i, y*_i).