Vychislitelnaya_matematika / Vychislitelnaya_matematika / Вычислительная математика / bilety_6-10

6. Полиномы Чебышева.

Полиномы Чебышева - система многочленов, определенных на отрезке [–1; 1]. Позволяют более равномерно распределить погрешность по всему интервалу. Многочлены Чебышева широко используются при аппроксимации функций. Полином Чебышева имеет вид:

1) рекуррентного отношение

2) Многочлены Чебышева первого рода могут быть также определены с помощью равенства:

n = 1. По определению арккосинуса, arccosx = α , поэтому cos(arccosx) = cosα = x.

n = 2. Надо вычислить cos(2arccosx). Снова введя обозначение arccosx = α, приходим к задаче найти сos2α, зная, что cosα = x. Поскольку сos2α = 2cos²α – 1, получаем, что cos(2arccosx) = 2х² – 1.

n = 3. Аналогично, используя формулу косинуса тройного угла cos3α = 4cos³α – 3cosα, получаем, что cos(3arccosx) = 4x³ – 3x.

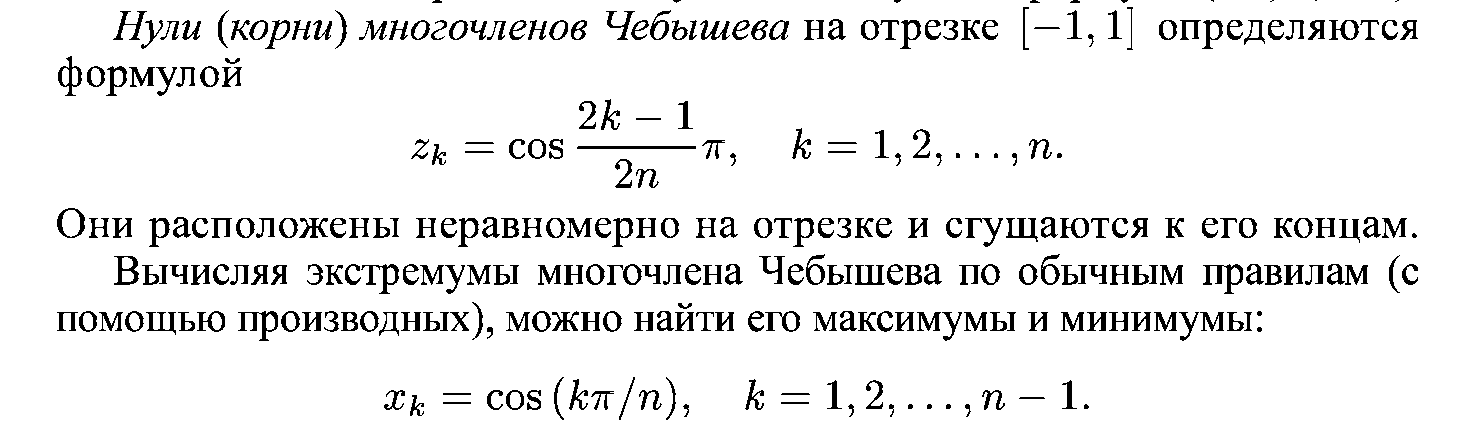
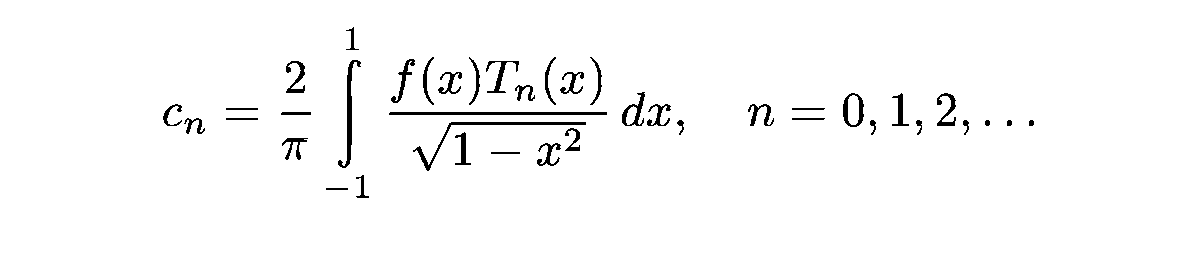
Ошибки:

По сравнению с рядом Тейлора максимальная ошибка меньше и она распределена равномерно.

7. Вычисление полиномов. Правило Горнера.

Схема Горнера (или правило Горнера, метод Горнера) — алгоритм вычисления значения многочлена, записанного в виде суммы мономов (одночленов), при заданном значении переменной. Метод Горнера позволяет найти корни многочлена, а также вычислить производные полинома в заданной точке.

Дан многочлен вида:  

p (x) = a₀+a₁x+a₂x²+…+a_nxⁿ

Если все честно считать, т. е. находить значения каждого члена и суммировать их, то при больших n потребуется выполнить большое число операций (n² + n/2 умножений и n сложений). Для исключения возведения x в степень в каждом члене многочлен целесообразно переписать в другом виде.

Вынесем за скобки x всюду, где это возможно:

p(x) =a0+x(a1+x(a2+…+x(an-1+x(an))…))

Прием, с помощью которого многочлен представляется в таком виде, называется схемой Горнера.

Вычисления по данной формуле производятся в соответствии с заданным порядком действий. Для вычисления полинома по правилу Горнера требуется n сложений и n умножений. Во многих практических расчетах применение правила Горнера не только экономит машинное время, но и повышает машинное время за счет уменьшения верхнего предела ошибки округления.

8. Рациональные приближения и непрерывные дроби.

Некоторые функции нельзя с достаточной точностью приблизить полиномами; в некоторых случаях бывает так, что полиномиальное приближение очень медленно сходится. Есть другой способ представления функции – рациональное приближение, которое соответствует отношению двух многочленов.

Рассмотрим разложение функции в ряд Тейлора:

f(x)=a₀+a₁x+a₂x²+…+a₇x⁷+… (1)

Запишем f(x) в виде частного от деления двух полиномов третьего порядка:

f(x)= (2)

(в знаменателе мы сократили первую константу и получили +1)

Приравнивая (1) и (2) получаем:

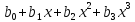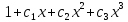= ()( a₀+a₁x+a₂x²+…+a₇x⁷+…)

Раскрывая скобки и приравнивая коэффициенты при одинаковых степенях x, получаем:

x⁰: b₀=a₀

x¹: b₁=a₁+c₁a₀

x²: b₂=a₂+c₁a₁+a₀c₂

x³: b₃=a₃+a₂c₁+a₁c₂+a₀c₃

x⁴: 0=a₄+a₃c₁+a₂c₂+a₁c₃

x⁵: 0=a₅+a₄c₁+a₃c₂+a₂c₃

x⁶: 0=a₆+a₅c₁+a₄c₂+a₃c₃

Таким образом мы получили семь уравнений для семи неизвестных b₀,b₁,b₂,b₃,c₁,c₂,c₃

Ошибки:

Вычислим, каким был коэффициент b7, если бы он был включен в это приближение, и разделим его на величину знаменателя:

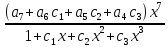
Эта оценка годится только для ошибки ограничения и не включает ошибку округления, но обычно последняя гораздо меньше ошибки ограничения.

Рациональные приближения обычно вычисляются с помощью эквивалентной непрерывной дроби.

Непрерывная дробь — это математическое выражение вида

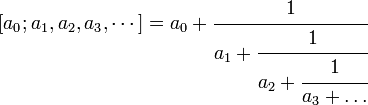
где a₀ есть целое число и все остальные a_n натуральные числа. Любое вещественное число можно представить в виде непрерывной дроби (конечной или бесконечной).

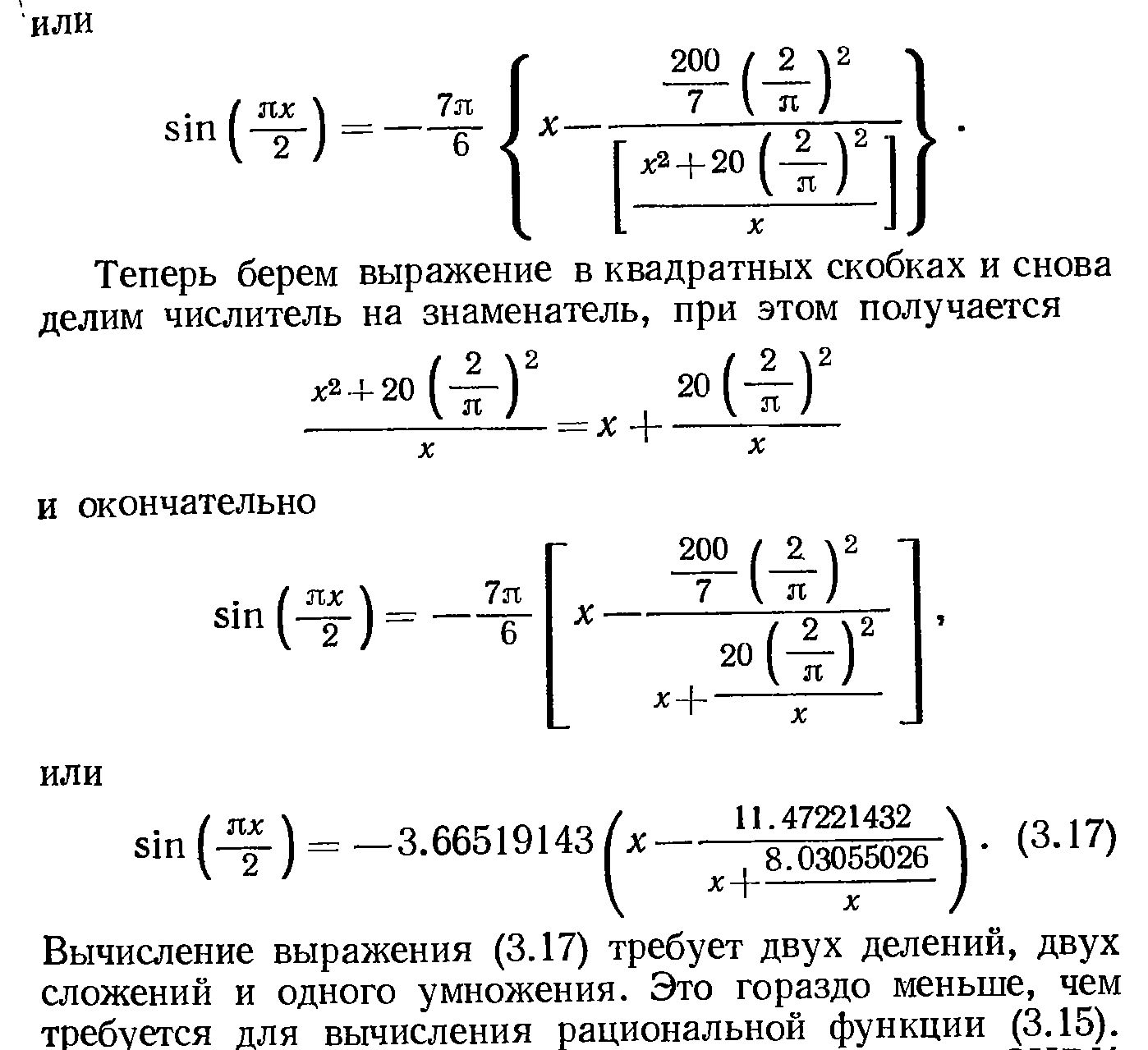
Для того чтобы проиллюстрировать этот метод, рассмотрим функцию синуса:

(3.15 – в таком виде можно записать, т.к. sin – нечетная функция. Мы представляем функцию в виде дробно-рационального выражения в соответствии с (2). В числителе может оставить только члены с нечетными степенями х, а в знаменателе – с четными.)

9. Численное решение уравнений. Метод последовательных приближений.

Если имеется некоторая функция F(x), то иногда бывает необходимо найти такие значения аргумента x, для которых F(x)=0. Не для всех функций есть аналитическая формула для нахождения корней (например, как у квадратного уравнения). Поэтому приходится пользоваться приближенными методами нахождения корней, которые состоят из двух этапов:

1. Отыскание приближенного значения корня.

2. Уточнение приближенного значения до некоторой заданной степени точности.

Численный метод, в котором производится последовательное уточнение первого начального грубого приближения, называется методом итераций. Если при последовательных итерациях получаются значения, которые все ближе и ближе приближаются к истинному значению корня, то говорят, что метод сходится.

Метод последовательных приближений

Предположим, что уравнение F(x)=0 переписано в виде

x=f(x).

Это преобразование можно сделать разными способами:

1. Если F(x)=x²-c=0,

Где с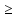0, то можно прибавить к правой и к левой частям x:

x=x²+x-c

2) Можно разделить все выражение на x и получить

x=

3) Можно преобразовать уравнение к следующему виду:

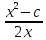x = x - = (x+)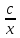

Корни этих уравнений равны

Для того чтобы вывести достаточные условия сходимости метода, рассмотрим следующие случаи:

1. Сначала рассмотрим геометрическое представление процесса. При решении уравнения x=f(x) отыскивается точка пересечения кривой y=f(x) и прямой y=x.

Случай 0<f’(x)<1

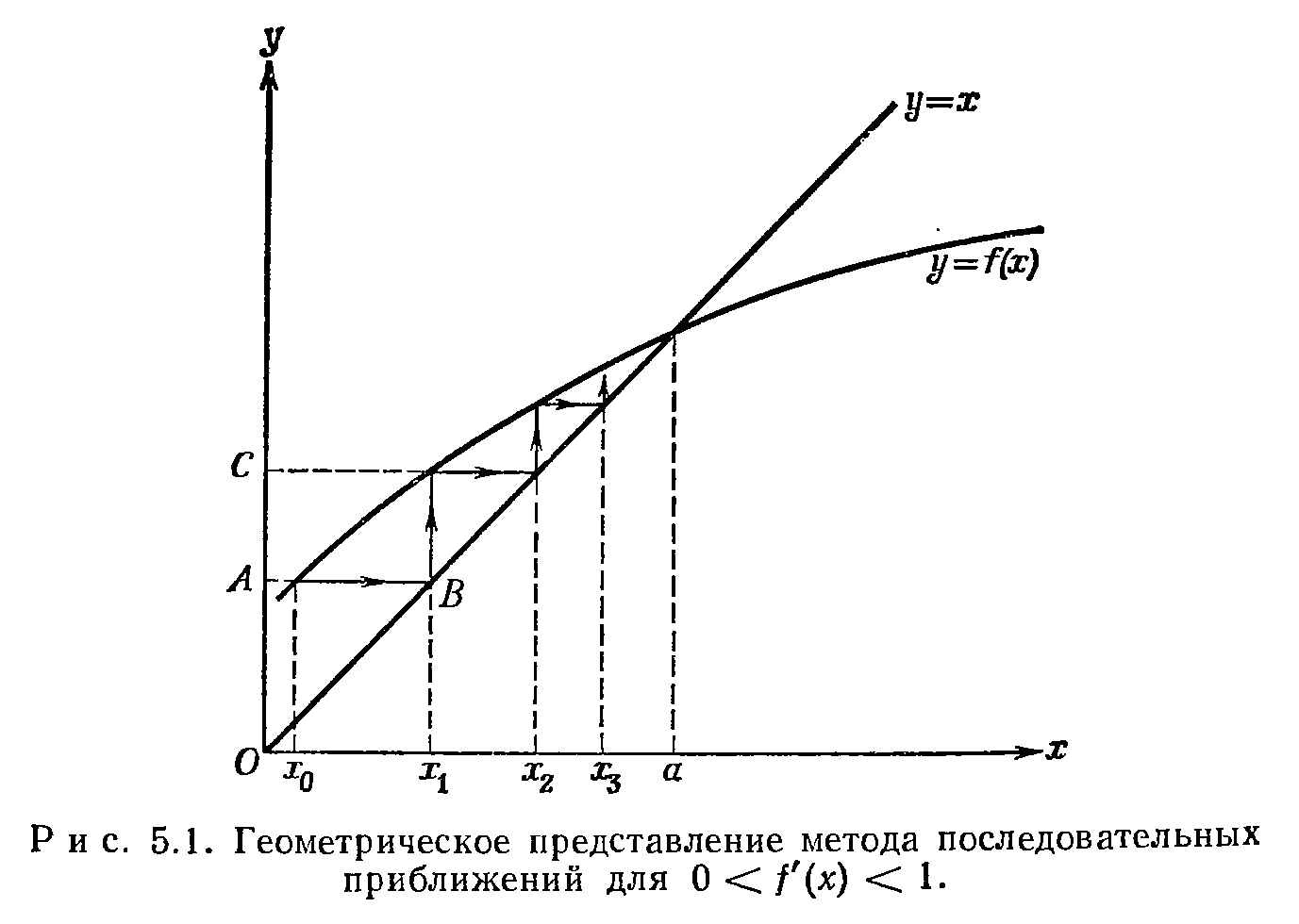
2. Случай 0>f’(x>-1

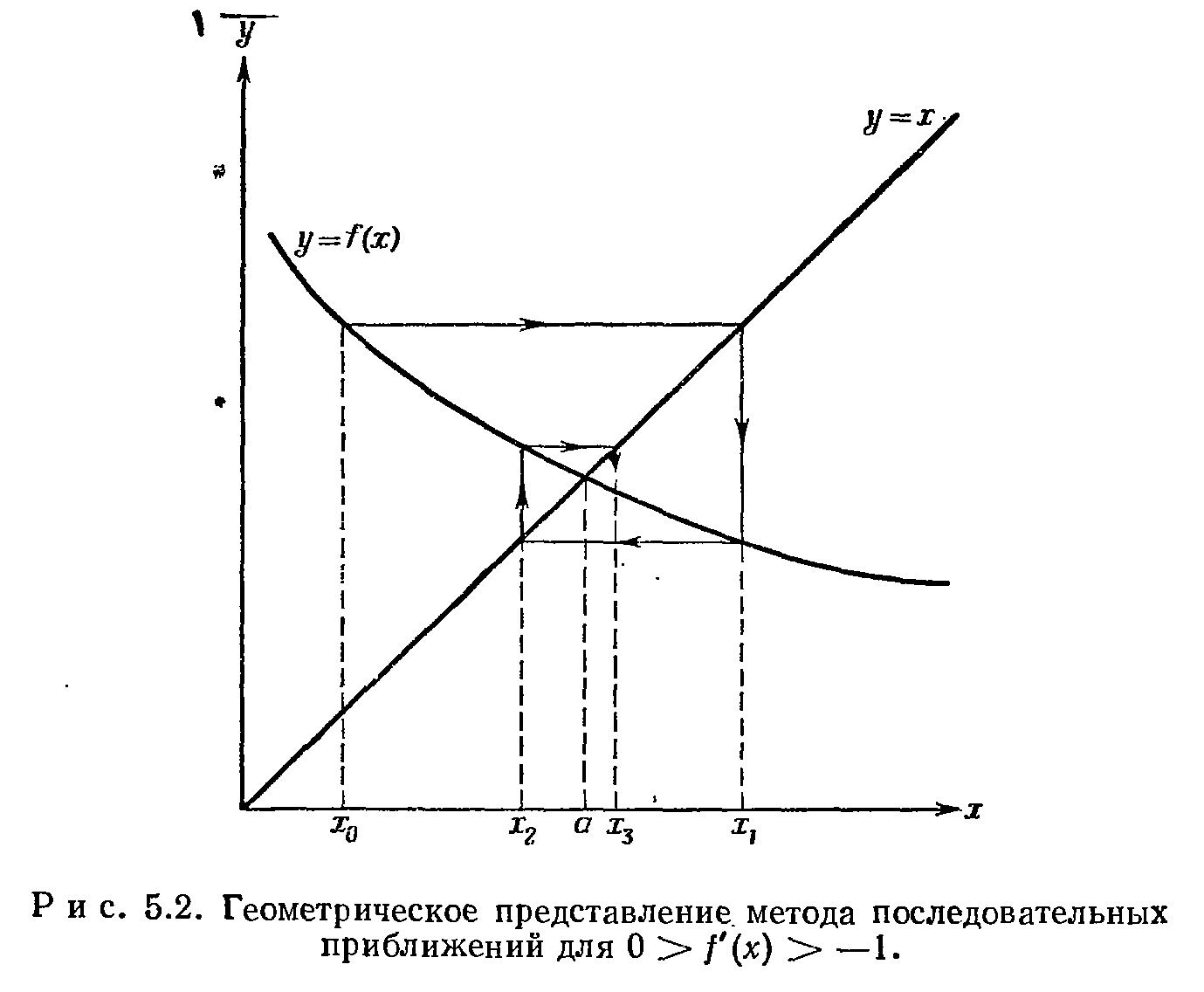
3) В случаях, когда производная функции больше 1 и меньше 1, то метод расходится. Каждое последующее значение x отстоит больше от истинного значения корня, чем предшествующее.

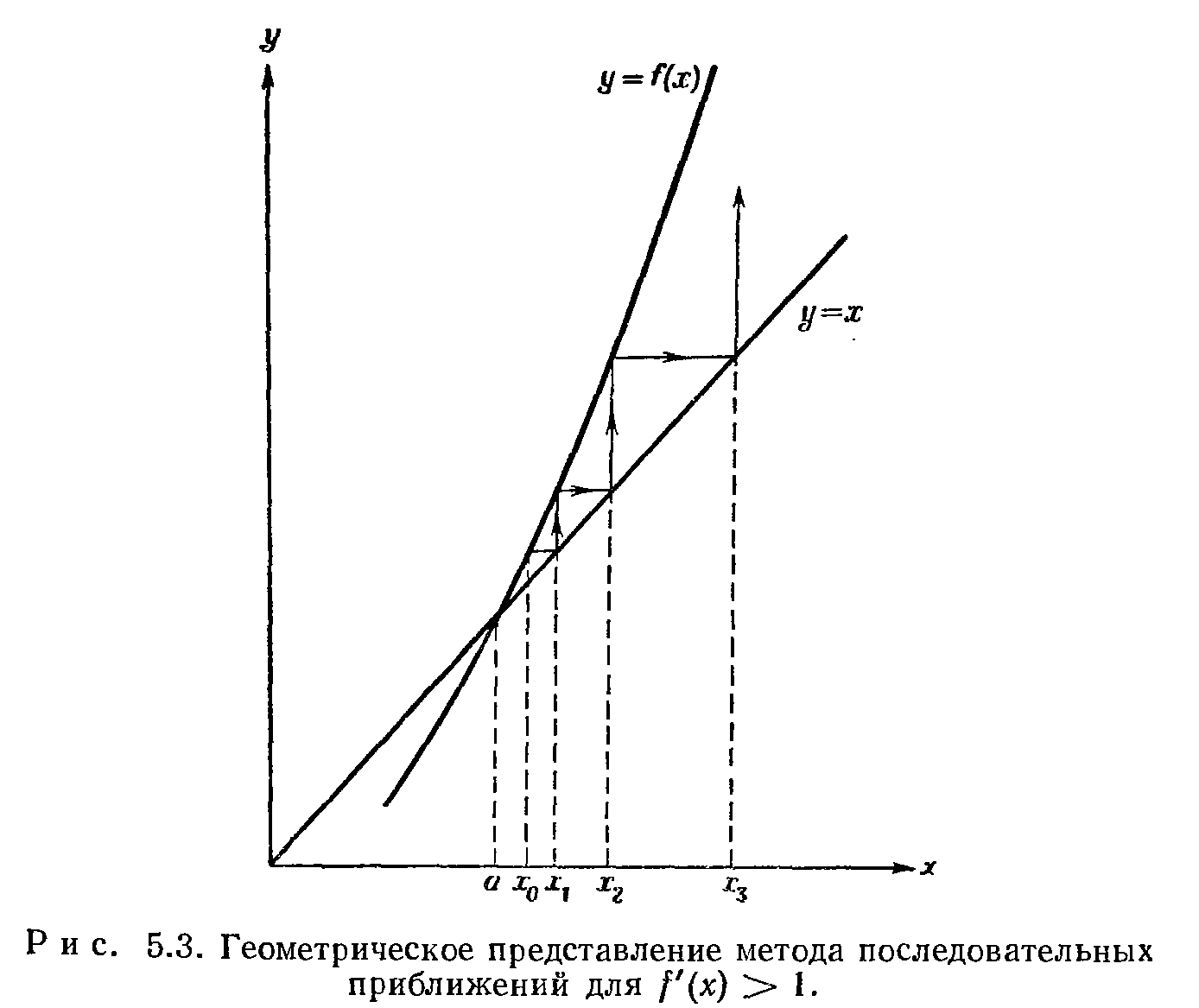
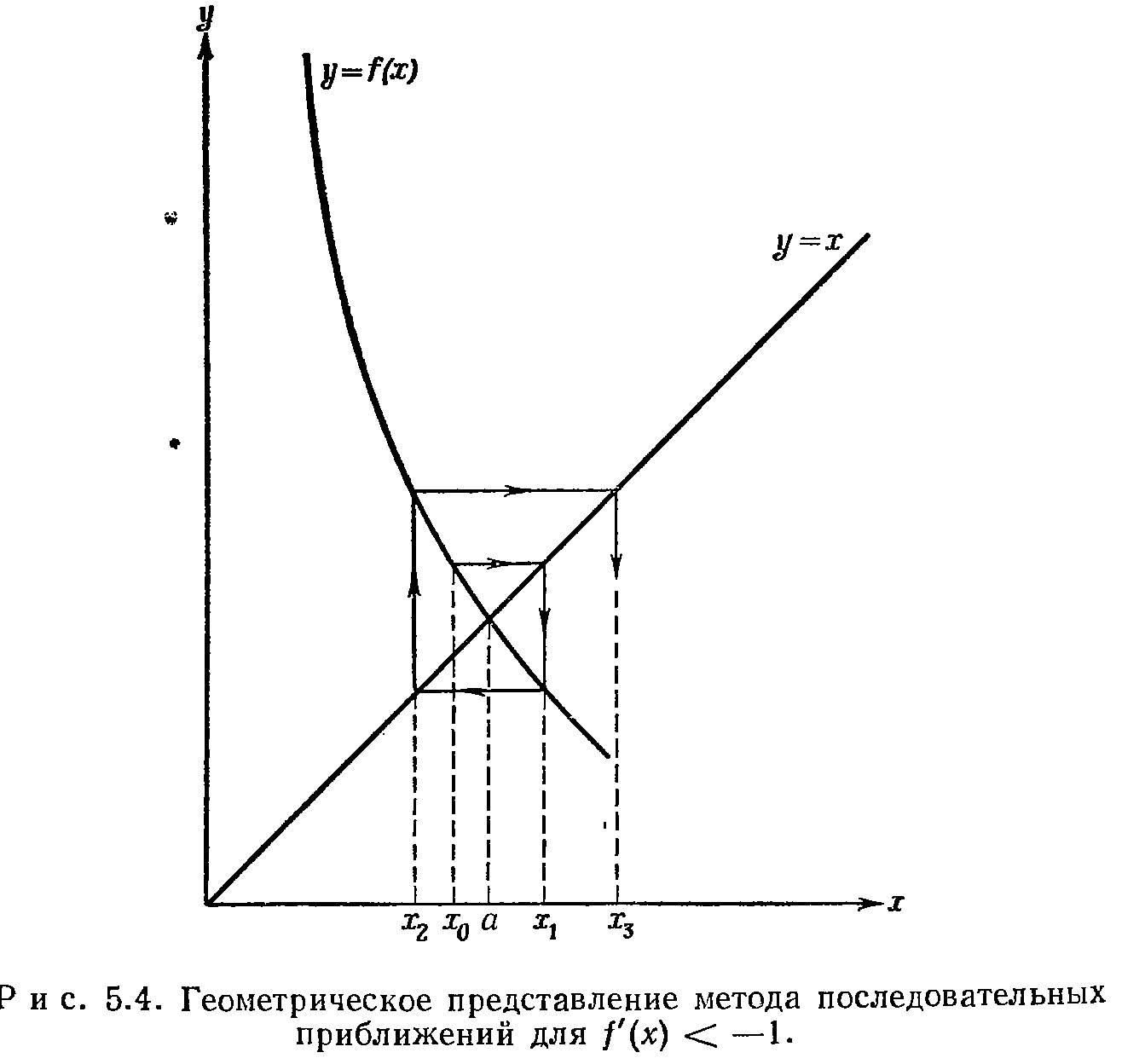
Итерации по формуле x_n=f(x_n-1) сходятся при условии, что производная f’(x) меньше 1 по абсолютной величине.

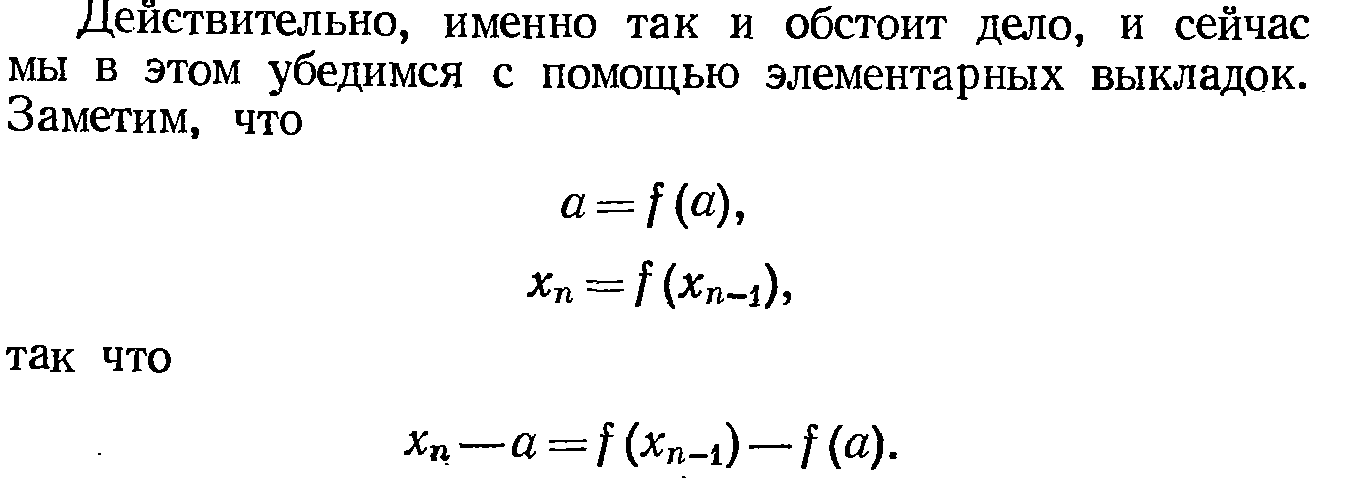
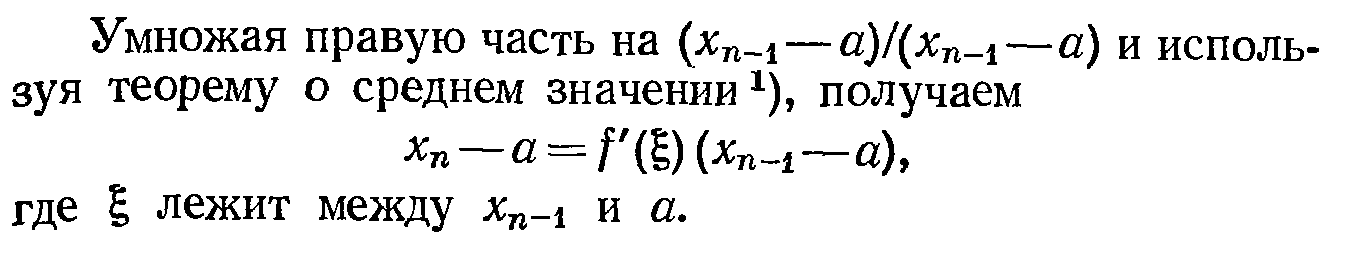
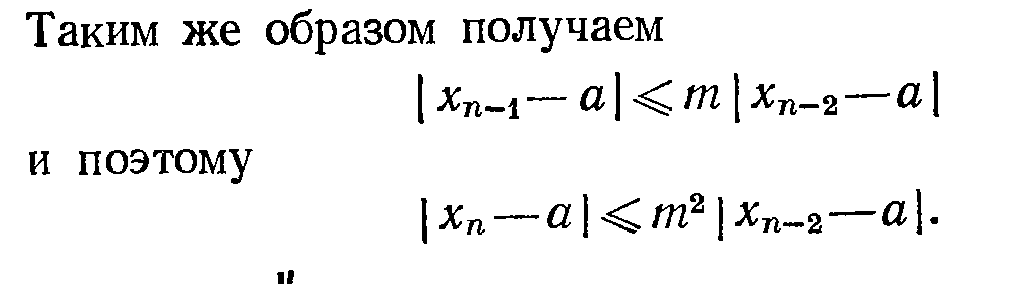
(Такая же лабуда есть про случай когда |f’(x)|>1. Но это задавали на дом, так что обойдемся общим тезисом)

Когда |f’(x)|>1величина |x_n-a| неограниченно возрастает с ростом n.

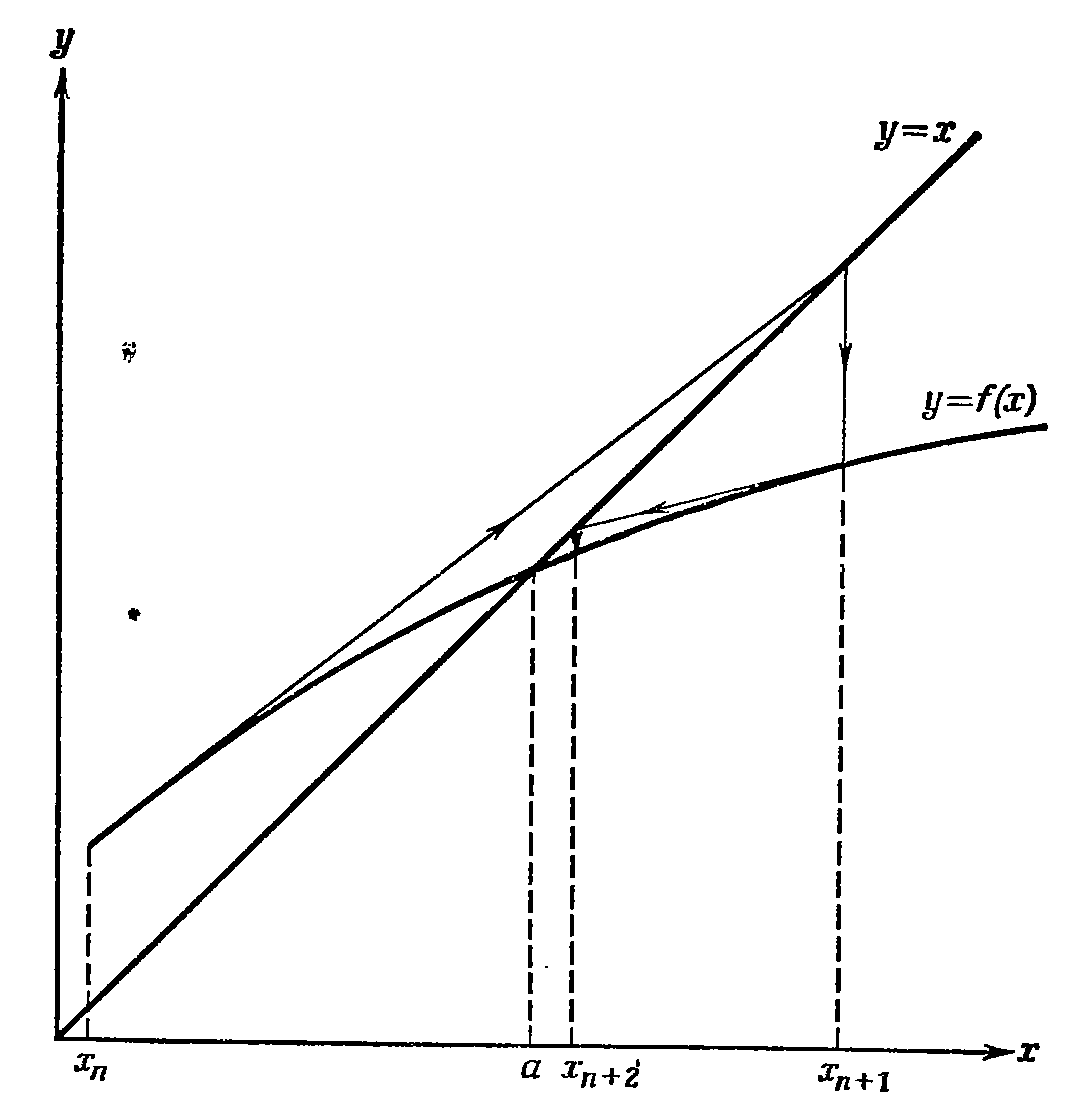
Усовершенствованный метод последовательных приближений

Из предыдущих графиков (когда метод сходился) видно, что, хотя каждое последующее значение x_n находится ближе к решению уравнения, чем предыдущее, все они сильно отличаются от корня. Можно было бы добиться более быстрой сходимости метода, если при каждой очередной итерации делать большую поправку к очередному значению x_n. Т.е. вместо того, чтобы полагать

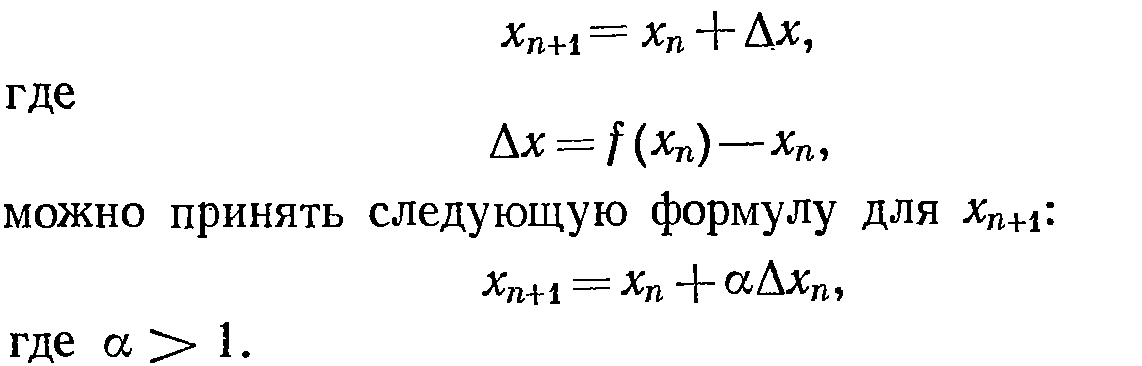
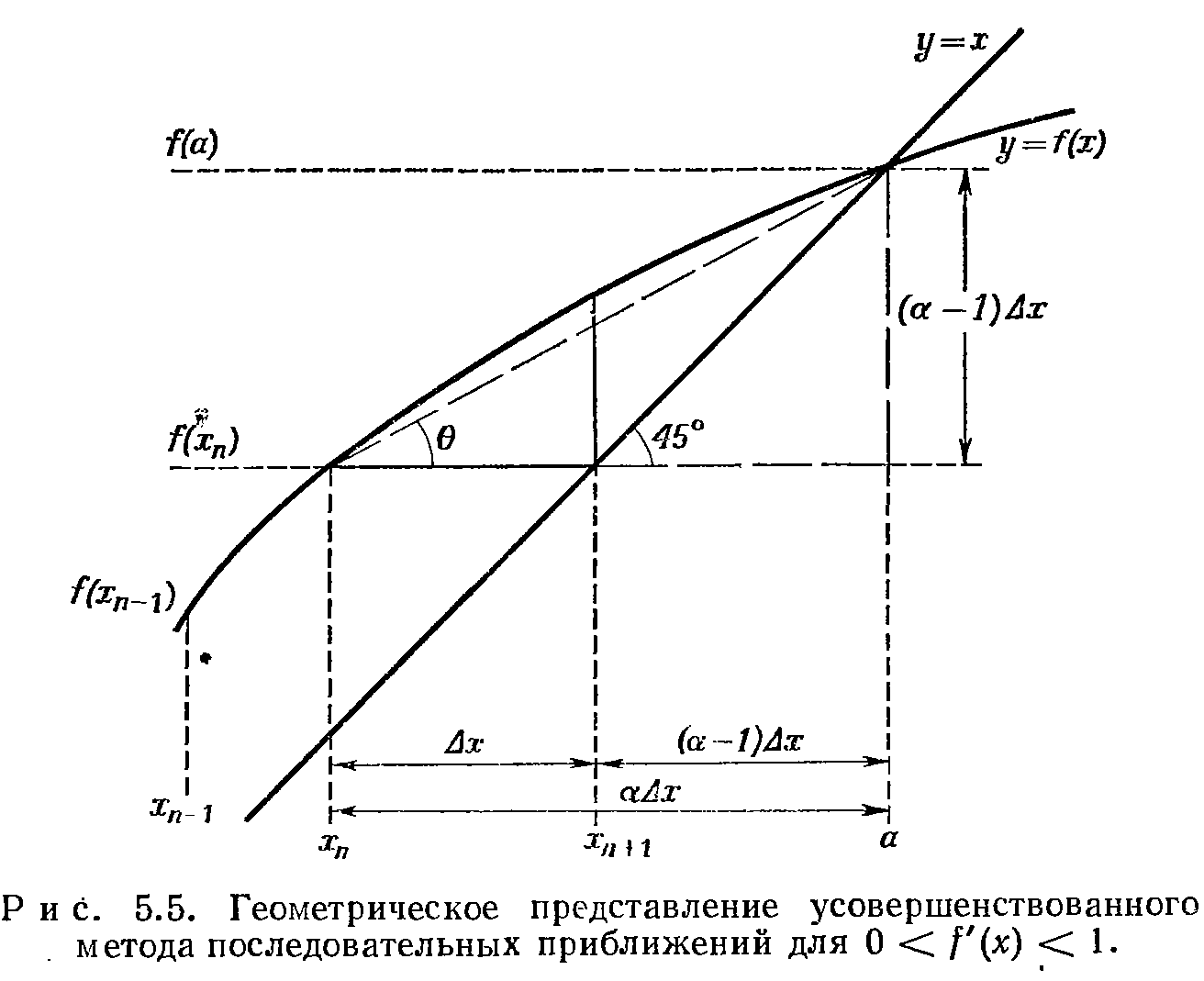
Наилучшим выбором 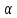следует признать тот, что изображен на рисунке, так

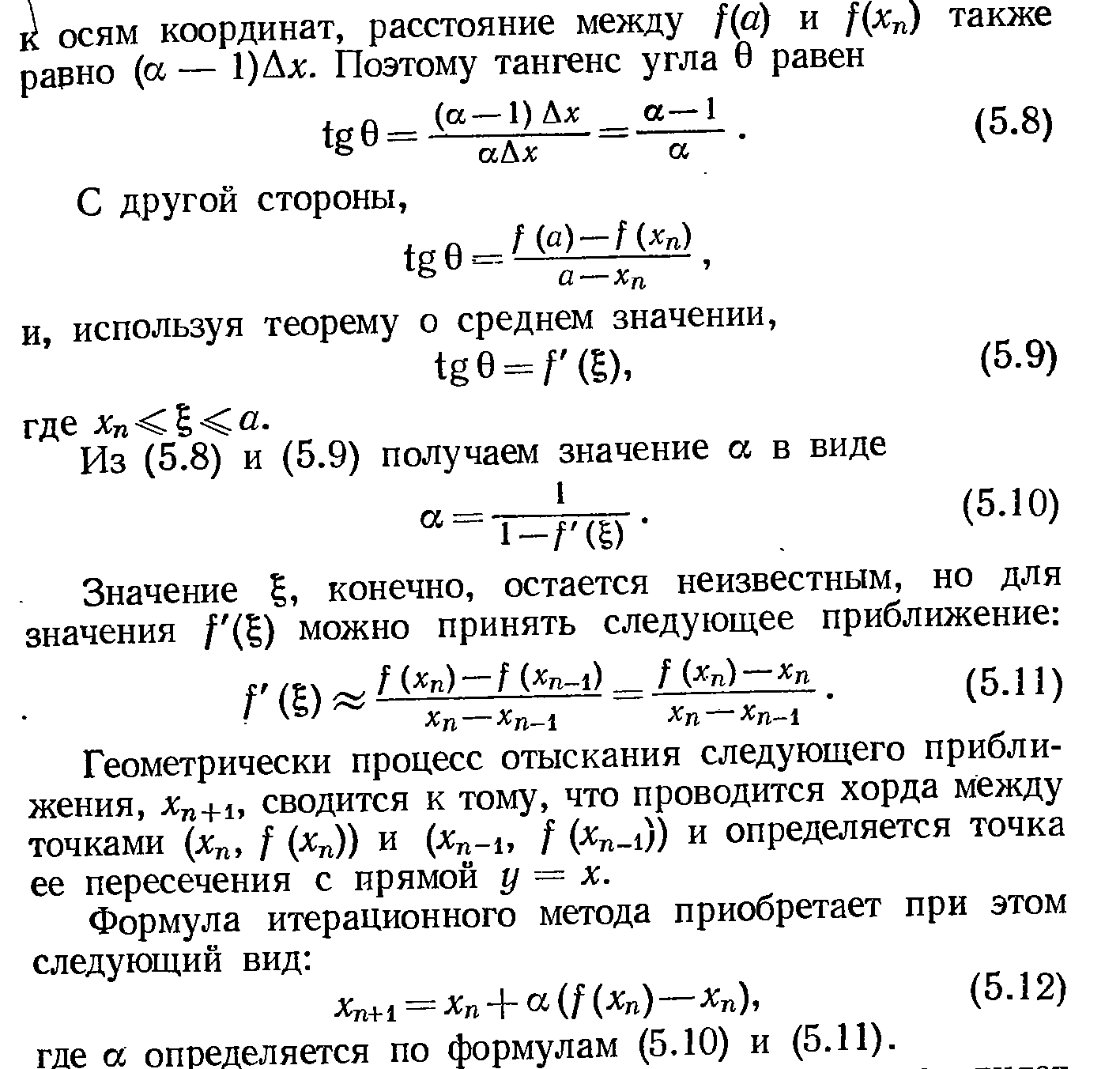
10. Метод Ньютона — Рафсона.

Метод Ньютона-Рафсона (или метод касательных)– это итерационный численный метод нахождения корня заданной функции f(x)

где f — произвольная функция с непрерывными первой и второй производными.

Берем некоторую точку ξ=x_n.

Тогда формула

(из метода последовательных приближений) принимает вид:

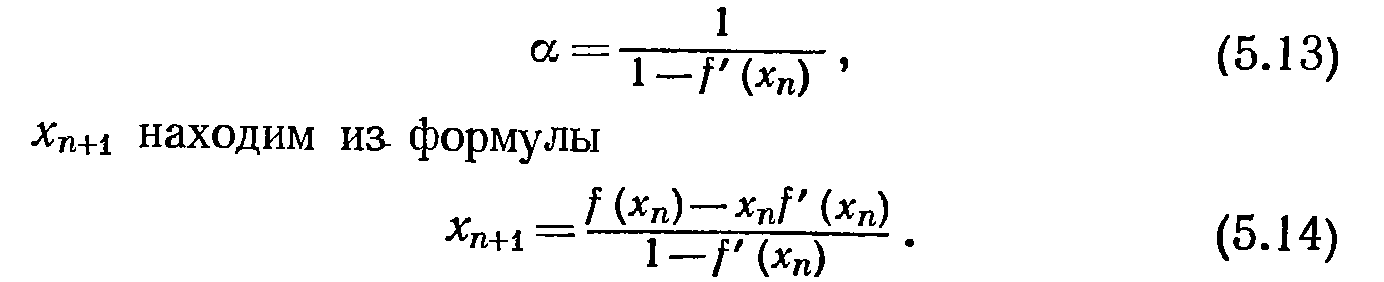
Последняя формула эквивалентна простому методу последовательных приближений

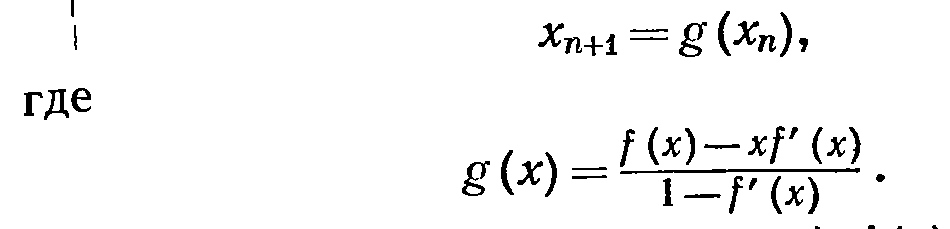
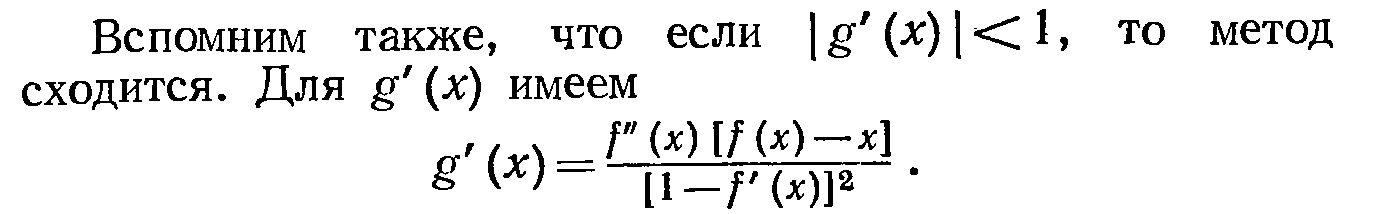
Поскольку f(x) подчиняется соотношению x=f(x)

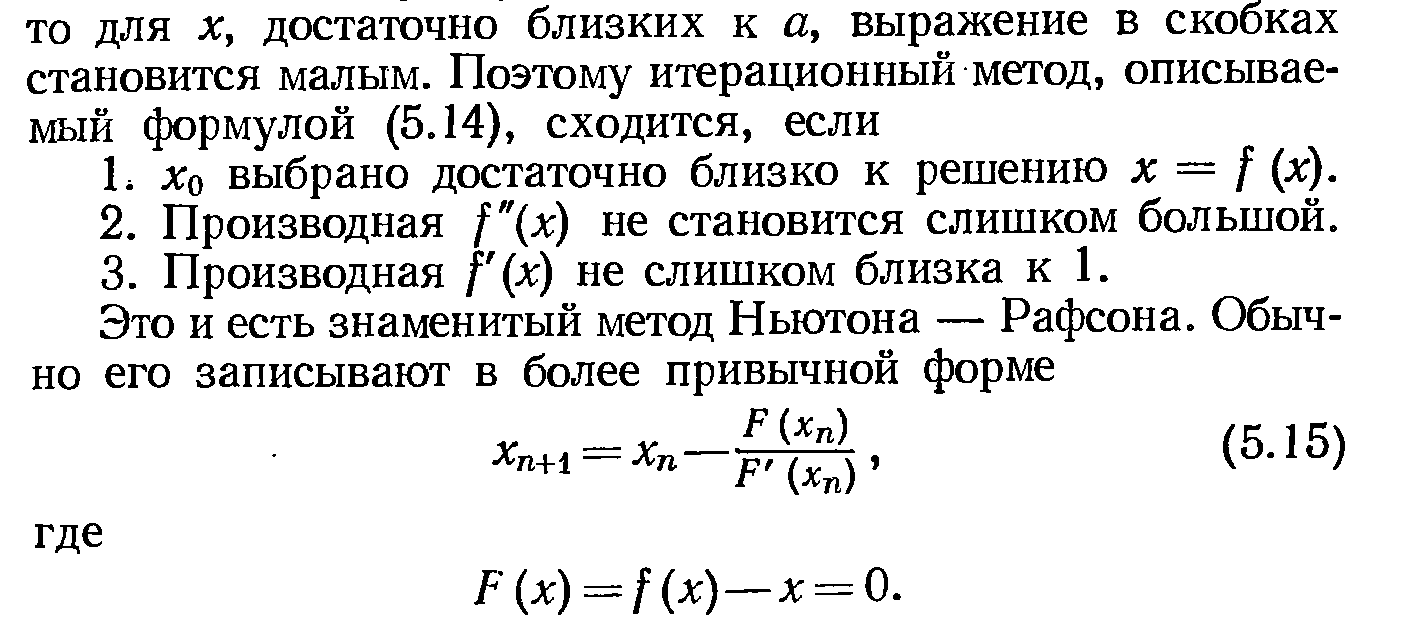
Условия сходимости принимают следующий вид:

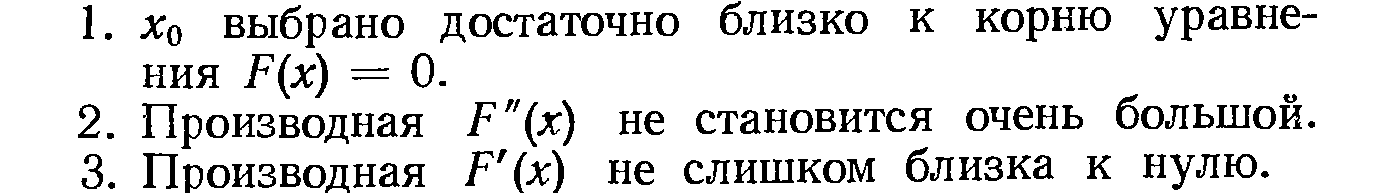
Последнее условие означает, что никакие два корня не находятся слишком близко один к другому.

Геометрическая интерпретация

Для F(x)=0 и формулы

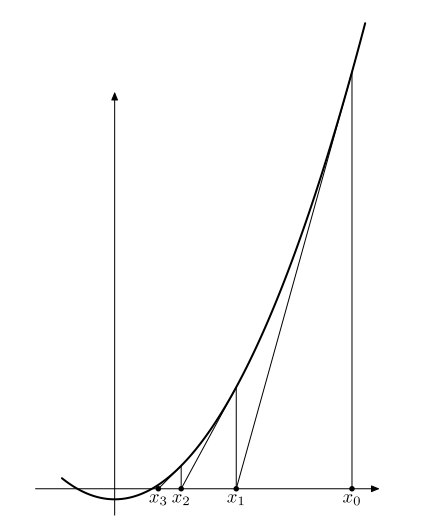
Мы берем пересечение касательной к графику в точке (x0, f(x0)) с осью абсцисс — это первое приближение к корню. Предположим, что мы получили очередное приближение x_n; тогда следующее приближение x_n+1 получается из предыдущего точно таким же способом, как первое из нулевого.

Поскольку уравнение касательной к графику функции y = f(x) в точке (x_n, f(x_n)) имеет вид y = f′(x_n )(x − x_n ) + f(x_n ), следующее приближение находится из условия

f′(x_n )(x_n+1 − x_n ) + f(x_n ) = 0.

(Hовое приближение x_n+1 является абсциссой точки пересечения касательной, проведенной в точке (x_n, f(x_n)) к графику функции f(x), с осью ОХ).

Окончательная формула для вычисления корня:

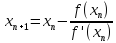
(Как выбирать нулевое приближение). В качестве нулевого приближения можно брать любую точку x₀ интервала отделимости, удовлетворяющую условию

f(x₀) · f′′(x₀) > 0.

Такая точка в интервале отделимости всегда найдётся, что гарантирует сходимость итераций. Если же условие не выполнено, то первое же приближение может выйти из интервала отделимости с непредсказуемыми последствиями.

Для f(x)=x

Ошибки округления

В методе касательных, как и в других итерационных методах решения уравнений, ошибка округления не накапливается. Общая ошибка округления равна ошибке, возникшей в последней итерации, и не зависит от арифметических операций, выполнявшихся в предыдущих итерациях.

Заключение

Метод касательных сходится быстрее, чем многие другие итерационные методы. Однако, главный недостаток метода - необходимость вычисления производной. Поэтому к функциям, заданным таблично и к функциям, у которых в некоторых точках отсутствует производная, метод неприменим.