2.7. Локальная теорема Лапласа

Пользоваться формулой Бернулли при большом числе испытаний n весьма непросто, так как приходится выполнять действия над огромными числами. Локальная теорема Лапласа дает формулу, которая позволяет приближенно найти вероятность того, что событиеА появитсяk раз вn испытаниях, если число испытаний велико.

Локальная теорема Лапласа. Если вероятность p появления события А в каждом испытании постоянна и не равна нулю или единице, то вероятность P_n (k) того, что событие А произойдет в n испытаниях k раз, приближенно равна (точность тем выше, чем больше n) значению функции

, при (2.4)

Введем обозначение

Тогда

P_n (k) ≈ y=(2.5)

В Приложении 2 дана таблица, в которой приведены значения функции φ(x) дляx > 0. Значенияφ(x) дляx < 0 можно получить из этой же таблицы, так как функцияφ(x) четная, т.е.φ(-x) =φ(x).

Пример 2.3. На некотором участке 20% деревьев определенного вида поражено вредителем. Найти вероятность P₄₀₀ (80) того, что из n = 400 случайно выбранных на участке деревьев k = 80 окажутся пораженными вредителем.

Решение.По условию задачи вероятность того, что одно случайно выбранное на участке дерево окажется пораженным вредителем, равнаp = 0,2. Вероятность того, что оно не будет поражено вредителем, равнаq = 1-p =0,8. В соответствии с локальной теоремой Лапласа

P₄₀₀(80) ≈

Значение xоказывается равным

x =

По таблице (Приложение 2) находим φ(0) = 0,3989. Значит

P₄₀₀(80) =

2.8. Интегральная теорема Лапласа.

Предположим, что проводится серия из n испытаний, в каждом из которых вероятность появления событияА постоянна и равнаp , причемp ≠ 0 иp ≠ 1. Интегральная теорема Лапласа дает вероятностьP_n(k₁ ,k₂ ) того, что событиеА произойдет вn испытаниях не менееk₁ и не болееk₂ раз (для краткости говорят "отk₁ доk₂ раз").

Интегральная теорема Лапласа. Если вероятность p появления события А в каждом испытании постоянна и не равна нулю или единице, то вероятность P_n (k₁ ,k₂) того, что событие А произойдет в n испытаниях от k₁ до k₂ раз, приближенно равна (точность тем выше, чем больше n)

P_n (k₁ , k₂) ≈ =

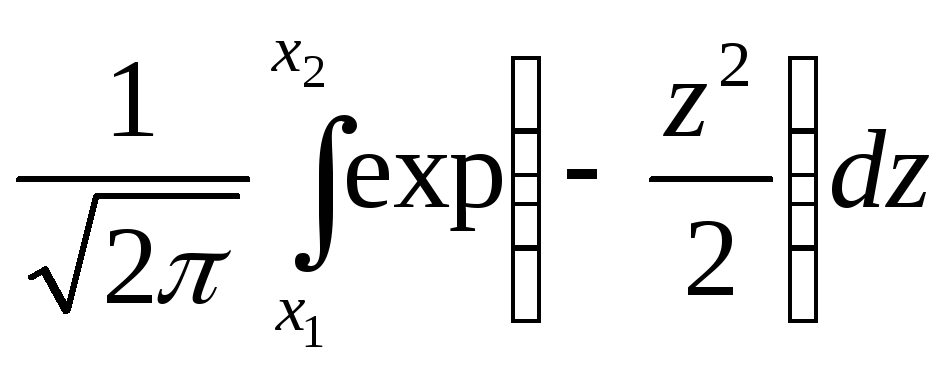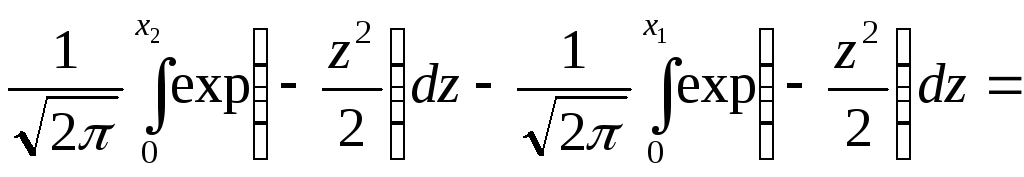= Ф (x₂) – Ф (x₁), (2.6)

где

x₁ = иx₂ =

Интеграл Лапласа

Ф(x) =(2.7)

не выражается через элементарные функции. Его значения находят численными методами интегрирования. При решении задач значения интеграла (или функции) Лапласа Ф(x) берут из специальной таблицы (Приложение 3). В таблице даны значения функции Ф(x) только дляx промежутка 0 ≤x ≤ 5. Дляx > 5 с большой точностью можно принять

Ф(x) = 0,5. При отрицательныхx значения Ф(x) находят из этой же таблицы, т.к. функция Ф(x) нечетная, т.е. Ф(-x) = - Ф(x) .

Пример 2.4. На некотором участке 20% деревьев определенного вида поражено вредителем. Найти вероятность P₄₀₀ (70, 100) того, что среди n = 400 случайно выбранных на участке деревьев пораженными вредителем окажутся от k₁ = 70 до k₂ = 100 деревьев.

Решение.По условию задачи вероятность того, что одно случайно выбранное на участке дерево окажется пораженным вредителем, равнаp = 0,2. Вероятность того, что оно не будет поражено вредителем, равнаq = 1-p =0,8. Согласно интегральной теореме Лапласа

P₄₀₀(70, 100) ≈ Ф(x₂) – Ф(x₁),

где

;

Поэтому

P₄₀₀(70, 100) = Ф(2,5) – Ф(-1,25) = Ф(2,5) + Ф(1,25).

По таблице (Приложение 2) находим

Ф(2,5) = 0,4938, Ф(1,25) = 0,3944.

В итоге получаем

P₄₀₀(70, 100) = 0,4938 + 0,3944 = 0,8882.