4.5. Выборочный коэффициент корреляции

Коэффициент корреляции вводится как величина, которая служит мерой тесноты (силы) линейной корреляционной зависимости признаков.

Рассмотрим сначала эксперименты, в которых одновременно измеряются только две величины (обозначим их Y иX ). Пусть проведеноn независимых совместных измерений признаковY иX , в результате которых полученоnпар чисел:

(x₁, y₁), (x₂, y₂), (x₃, y₃), …, (x_i , y_i ), …, (x_n, y_n). (4.7)

Такую совокупность пар чисел можно рассматривать как случайную выборку из генеральной совокупности всех возможных значений пары (Y ,X). Поэтому получаемое по этим данным значение коэффициента корреляции называют выборочным.

Выборочный коэффициент корреляции определяется равенством

, (4.8)

где y_i - экспериментальное значение величиныY , соответствующееx_i ;

n – объем выборки;

- выборочные средние признаковX иY ;

-выборочныесредние квадратичные отклонения признаковX иY .

Если вместо выборочных использовать исправленныесредние квадратичные отклоненияs_x,s_y , то вычисление выборочного коэффициента корреляции производится по формуле

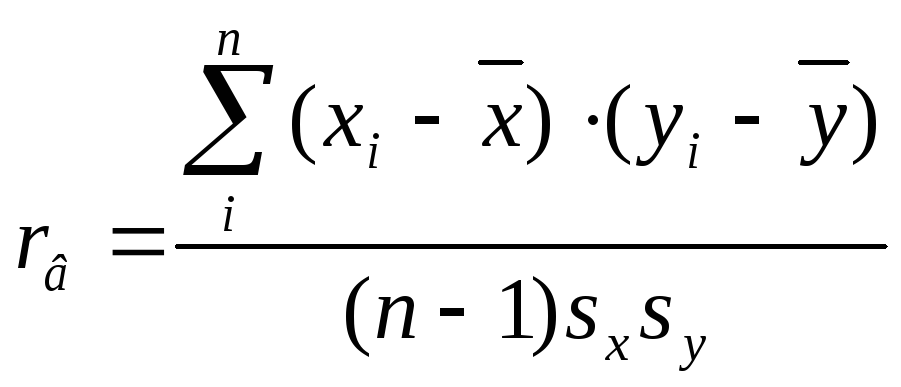. (4.9)

Почему введенное таким образом выражение для r_в способно служить мерой тесноты корреляционной связи? Дело в том, что выражение дляr_в является суммой произведений так называемых нормированных отклонений. Нормированное отклонениеt(x_i) вариантыx_iесть разность между значениемx_iварианты и ее средним значением, отнесенная к среднему квадратичному отклонению этой варианты:. Аналогичноесть нормированное отклонение вариантыy_i . Используя нормированные отклонения, выражение дляr_вможно представить в видеr_в=. При коррелированности (т.е. наличии сопряженности изменения) признаковX иY величиныt(x_i) иt(y_i) принимают положительные и отрицательные значения некоторым регулярным образом, поэтому произведенияt(x_i) t(y_i) входят вбольшей частью с одинаковым знаком, что обеспечивает отличиеr_в от нуля. Кроме того, при коррелированности признаковX иY и модули величинt(x_i) иt(y_i) меняются согласованно: например, в случае линейной корреляции большим по модулю значениямt(x_i) соответствуют, как правило, большие по модулю значения t(y_i), что также приводит к отличиюr_в от нуля. Наоборот, при отсутствии корреляции знаки величинt(x_i) иt(y_i) будут меняться чисто случайным образом, из-за чего число положительных слагаемых в суммебудет примерно равно числу отрицательных, что приведет к их взаимному сокращению и равенствуr_в = 0.

Существует много различных рабочих формул для вычисления r_в прямым способом, т.е. при непосредственном использовании полученных в результате измерений значенийx_i иy_i . Здесь приведены лишь наиболее употребимые из них. Выражение

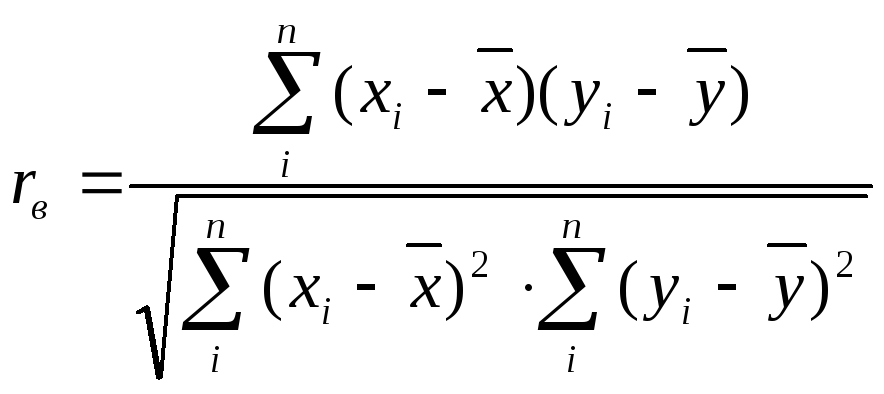(4.10)

получается из (4.8) заменой ивыражениямиив соответствии с их определением. В этом выражении используются только отклонения вариант от средних.

Еще одна формула для вычисления r_вполучается в результате преобразования числителя в выражении (4.9):

Отсюда получаем

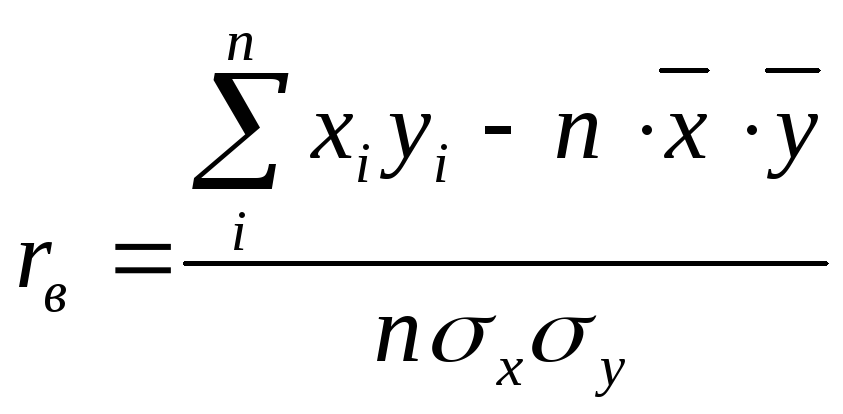(4.11)

или

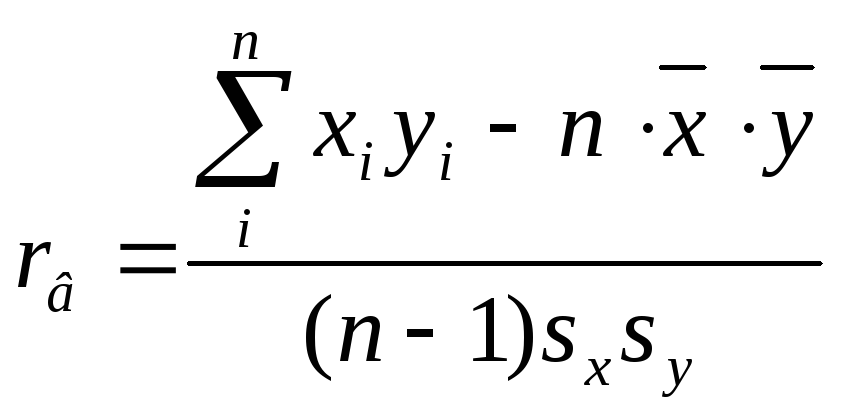. (4.12)

Формулы (4.8 ), (4.9) и (4.10 ) для вычисления выборочного коэффициента корреляции применимы и в случаях, когда данные измерений не могут быть сгруппированы, из-за того, что различные значения x_i иy_i величинX иY наблюдаются по одному разу, и в тех случаях, когда данные могли бы быть сгруппированы, но решено группировку не делать.

Если данные n экспериментов по совместному измерению значений величинY иX сгруппированы и представлены в виде корреляционной таблицы (типа приведенной в 4.4.2.), то выборочный коэффициент корреляции удобно вычислять по формуле

, (4.13)

где x,y – варианты (наблюдавшиеся значения) признаковX иY ;

n_xy - частота (число появлений) наблюдавшейся пары вариант (x ,y );

n – объем выборки ();

- выборочные средние признаковX иY ;

- выборочные средние квадратичные отклонения признаковX иY .

Если использовать исправленныесредние квадратичные отклоненияs_x,s_y , то

. (4.14)

Важно отметить, что выборочный коэффициент корреляции r_в и угловой коэффициентk прямой линии регрессии (4.4) связаны между собой соотношением

(4.15)

или

. (4.16)

Это выражение не только дает еще один способ вычисления коэффициента корреляции, но и явно указывает на то, что r_в является мерой именно линейной корреляционной связи.

Пример 4.3. Проверить прямым вычислением справедливость формулы (4.15) по данным примера 4.2.

Решение. По данным примера 4.2.

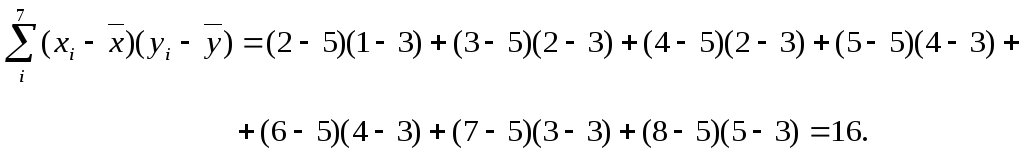
Выборочные дисперсии равны

,

.

Выборочные средние квадратичные отклонения равны

Отсюда

.

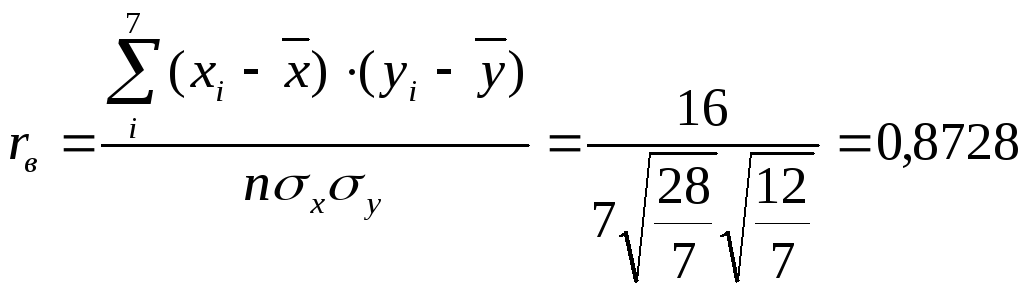С другой стороны

Если вместо выборочных использовать исправленные средние квадратичные отклонения, которые оказываются в данном случае равными s_x =,s_y = , то

Е

Какие значения r_в можно считать большими, а какие средними или малыми? Оказывается, что при наличии корреляции степень влияния изменений одного признака на изменения другого может быть выражена квадратом коэффициента корреляции. Это значит, что приr_в = 0,9 81% вариации одного признака обусловлен вариацией другого признака, в остальных же 19% случаев совпадение или несовпадение вариаций признаков по знаку и величине является чисто случайным. Приr_в = 0,3 такая обусловленность имеет место менее, чем для 10% вариаций. Таким образом, корреляцию (связь) принято считать: очень тесной, если; тесной, если; средней (значительной), если; умеренной, если; слабой, если

Изучаемые признаки X иYчасто имеют различную размерность, но коэффициент корреляцииr_весть всегда величинабезразмерная.