22. Математические характеристики деревьев
Свойства
Определим математические характеристики деревьев.
Свойство 1. В любом дереве между двумя его узлами существует один и только один путь их соединяющий.
Любые два узла дерева имеют ближайшего общего прародителя: узел лежащий на пути от каждого из этих узлов к корню. Ближайший общий прародитель обязательно существует, потому что им является либо корень дерева, либо корень меньшего поддерева, в котором они оба расположены.
Свойство 2 Дерево, имеющее N узлов, имеет N-1 связей.
Это вытекает из того, что каждый узел за исключением самого верхнего имеет связь со своим родителем.
Следующие два свойства относятся к бинарным деревьям.
Свойство 3 Бинарное дерево, имеющее N внутренних узлов, имеет N+1 внешних узлов.
Это можно доказать по индукции. Бинарное дерево, не имеющее внутренних узлов, имеет один внешний. Таким образом, свойство выполняется при N=0. Для N>0, бинарное дерево содержит k внутренних узлов в левом и N-k-1 внутренних узлов в правом поддеревьях, для какого-то k между 0 и N-1, так как корень является внутренним узлом. В соответствии с правилами индукции левое поддерево имеет k+1 внешних узлов, а правое N-k. В результате наше дерево имеет N+1 внешних узлов.
Свойство 4 Внешняя длина пути любого бинарного дерева имеющего N внутренних узлов на 2N больше чем внутреннего пути.
Заметим, что бинарное дерево может быть создано следующим образом: начнем с дерева состоящего только из корня. Затем повторим следующее N раз: выберем какой-нибудь внешний узел и заменим его внутренним с двумя внешними. Если внешний узел был на уровне k, то внутренняя длина пути дерева увеличится на k, а внешняя на k+2. В начале процесса внутренняя и внешняя длины пути равны 0 и в течение N-1 шагов длину его внешнего пути увеличивается по сравнению с внутренней на 2.
Наконец мы рассмотрим простое свойство «самого лучшего» сорта бинарных деревьев – полных деревьев.
Свойство 5 Высота полного бинарного
дерева имеющего N внутренних узлов
приближенно равна
.
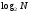Если высота полного бинарного дерева n, то, по определению полноты, для Nсправедливо условие
Отсюда следует, что высота
дерева при N внутренних узлов примерно
.
23. Обход деревьев
Обход Деревьев
Когда дерево создано, нас интересует, как по нему путешествовать. Эта операция тривиальна для линейных списков по их определению, но для деревьев существует множество различных подходов, главное различие между которыми, это порядок посещения узлов в дереве. Как мы увидим дальше, для различных задач подходит различный порядок обхода.
Сосредоточимся пока на обходе бинарных деревьях.
Первый метод, который мы рассмотрим, носит название «текущий – первым». Он может быть использован для того, чтобы написать выражение на Error: Reference source not found в форме префикса. Определяется он простым рекурсивным правилом: «посети корень, затем левое поддерево, затем правое поддерево». Здесь приведена реализация этого метода, основанная на стеке:
procedure traverse( t : link ); begin StackInit; push(t); repeat t := pop; visit( t ); if ( t <> z ) then begin push( t^.r ); push( t^.l ); end; until stackempty; end;
Следуя правилу, мы должны посетить сначала корень, что мы и делаем, положив его сначала на стек, а затем при входе в цикл, снимая его. Затем, мы спасаем правое, а после него левое поддерева на стек, и в начале цикла поднимаем со стека сначала левое поддерево, а обойдя его, принимаемся за правое. Когда стек оказывается пуст, процедура заканчивает свою работу. На рис. 2. демонстрируется порядок посещения элементов в дереве при этом методе.
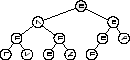
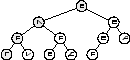
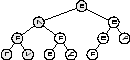
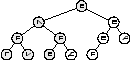
Обход методом «текущий первым».
Второй метод называется «текущий – между» или «симметричное посещение». Как видно из названия его определяет правило: «посети сначала левое поддерево, затем текущий узел, затем правое поддерево». рис. 3. демонстрирует порядок посещения элементов в дереве при этом методе.
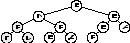
Обход "симметричным" методом.
Третий метод называется "текущий – последним". Из названия ясно его правило: «посети сначала левое поддерево, затем правое поддерево, затем текущий узел». На рис. 4. изображен порядок посещения элементов дерева при этом методе.
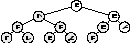
Обход методом «текущий последним».
Наконец последний метод это так называемое поуровневое посещение. Реализация этого метода использует FIFO очередь вместо стека, и определяется он простым правилом: «слева направо – сверху вниз». Ниже приведена простая реализация этого метода:
procedure traverse(t:link); begin QueueInitialize;put(t); repeat t:=get;visit(t); if(t<>z)then begin put(t^.r);put(t^.l); end; untilQueueEmpty;end;
24. быстрая сортировка, характеристика производительности быстрой сортировки