6. 2 Замечательные пределы

1. Первый замечательный предел .

Доказательство:

рис .6.3

Рассмотрим единичную окружность. Пусть . Тогда. Из рисунка видно, что,

, . Тогда.

Так как , то. В силу того, что, получим. Это неравенство имеет место и для, т.к. функцииичетные. Легко показать, что.

Следствия

1. 

2. 

3. 

4. ()

5. 

Доказательство (5): .

2. Второй замечательный предел .

Доказательство:

Пусть . Положим. Тогдаили. Имеет место неравенство. Так как, то. Из неравенствав силу того, чтоиимеем.

Теперь пусть . Положим. Теперь. Тогда.

Следствия

1. .

2. .

3, в частности,.

4. , в частности.Доказательство (4): .

5. Доказательство (5):

. 

6. 3 Непрерывность функции в точке

Определение 1Пусть функция определена в некоторой окрестноститочки. Говорят, что функциянепрерывна в точке , если выполняется соотношение.

Определение 2

Функция непрерывна в точке , если.

Определение 2*

Функция непрерывна в точке , если.

Определение 3

Функция называетсябесконечно малой в точке , если.

Определение 4

Функция называетсянепрерывной в точке , если бесконечно малому приращениюаргумента соответствует бесконечно малое приращениефункции, т.е., где.

Свойства непрерывных функций в точке

Теорема 1

Пусть функции непрерывны в точке. Тогданепрерывны в точке.

Доказательство:

Докажем непрерывность произведения в точке. Так как функцииинепрерывны в точке, то можно представить, где- БМФ в точке. Тогда. Перейдем к пределу при. Получим.

Определение 5

Пусть функция определена в некоторой окрестности точки, аопределена в некоторой окрестности точки. Тогда функцияназываетсякомпозицией функции или сложной функцией, а операция образования называется операцией композиции.

Замечание 1 Так как , то, т.е. для непрерывной функции знак функции и предела можно менять местами.

Теорема 2. О непрерывности композиции функций

Пусть функция непрерывна в точке; функциянепрерывна в точке, причем. Тогданепрерывна в точке.

Доказательство:

По условию . Рассмотрим.

Теорема. Любая элементарная функция непрерывна на своей области определения.

Пример Покажем непрерывность в любой точкечисловой оси.

Рассмотрим . Тогда, что значит. Мы воспользовались тем, что. Действительно, если, топри. Тогда при. Если же, то.

Определение 6 Точка , в окрестности которой определена функция, причем в самой точкеможет быть не определена, называетсяточкой разрыва функции , еслине является непрерывной в точке.

Точки разрыва функции бывают:

- точкой устранимого разрыва, если существуют , причем;

- точкой разрыва I рода, если существуют , но;

- точкой разрыва II рода, если хотя бы один из односторонних пределов илибесконечен или не существует.

рис. 6.4

Пример

Рассмотрим функцию . Данная функцияопределена при. В точкефункция имеет разрыв. Найдеми.

Тогда, доопределив функцию в точке, получим функцию, являющейся непрерывной в точке.

Таким образом, мы устранили разрыв. Поэтому точка является точкой устранимого разрыва функции.

Пример

Рассмотрим функцию

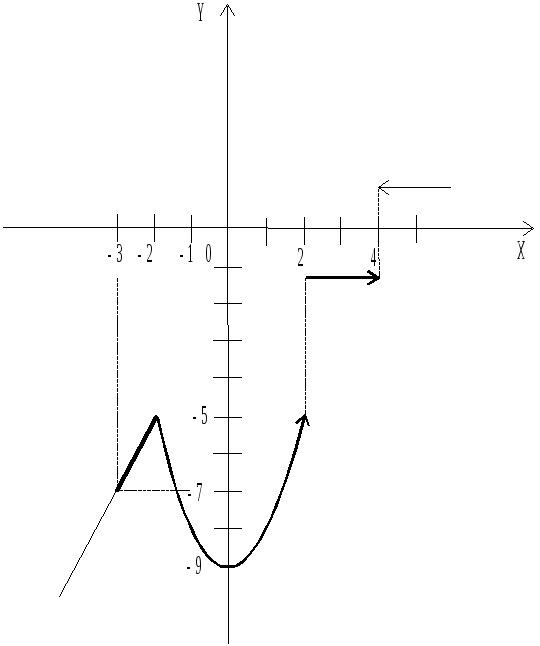
Каждая составная часть этой функции, кроме последней, непрерывна. Следовательно, надо исследовать функцию на стыках и в точке . Вычислим все односторонние пределы:

1. ;

- точка непрерывности;

2) ;

- точка разрыва I

рода;

3)

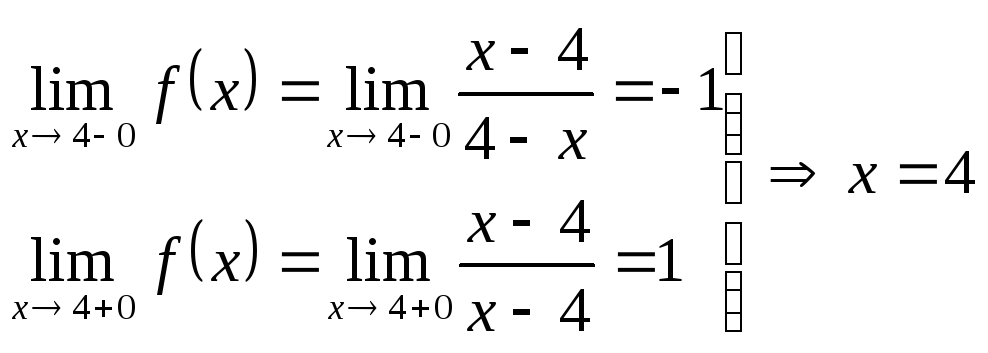–точка разрыва I рода.

Пример Рассмотрим функцию .

Функция имеет разрыв только в точке. Исследуем его:. Тогда- точка разрываII рода.

рис. 6.6