Глава VIII Интегральное исчисление функций одного переменного

Одной из основных задач дифференциального исчисления является отыскание производной заданной функции. Разнообразные задачи математического анализа и его различные приложения в геометрии, механике, физике приводят к обратной задаче: по данной функциинайти такую функцию, что.Восстановление функции по известной производной этой функции – одна из основных задач интегрального исчисления.

П.1 Понятие первообразной

Определение 1. Функция называетсяпервообразной функции на некотором интервале, если:

1. функция дифференцируема на;

2. выполняется равенство .

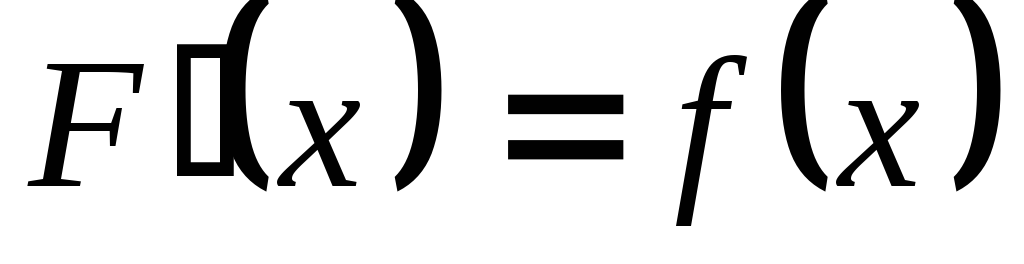
Пример. Функция является первообразной для функции, так как.

Пример. Функция является первообразной для функциипри.

Пример. Функция является первообразной для функциипри.

Задача отыскания по заданной функции ее первообразной решается неоднозначно. Действительно, если- первообразная для, т.е., то функция, где, также является первообразной для, так как.

Покажем, что множество функций исчерпывает все первообразные функции.

Теорема 1. Пусть идве первообразные функции. Тогда, где.

Доказательство:

Пусть . Тогда. По следствию из теоремы Лагранжа условиевлечет за собой, т.е.. ■

Замечание. Подчеркнем, что по определению первообразной функция должна быть дифференцируемой на интервале, т.е. не любую функцию можно проинтегрировать на любом интервале.

Пример. Пусть . Тогда,, и на множествепри. Но на любом интервале, содержащем точку, функцияне дифференцируема, т.е. функцияне имеет первообразной на всей чиcловой оси.

Замечание. Функция является первообразной для функции, хотяопределена.

Замечание. Функция имеет первообразную

,т.е. не имеет первообразных на любом интервале, содержащем точку .

Определение 2. Совокупность всех первообразных функции называетсянеопределенным интегралом от функции на интервалеи обозначается, причем функциюназываютподынтегральной функцией, -подынтегральным выражением, а -переменной интегрирования.

Восстановление функции по ее производной или отыскание неопределенного интеграла от подынтегральной функции, называют интегрированием этой функции. Это операция, обратная дифференцированию. Для того, чтобы проверить, правильно ли выполнено интегрирование, достаточно продифференцировать результат и получить при этом подынтегральную функцию.

Геометрический смысл неопределенного интеграла

Пусть - неопределенный интеграл от функции. При конкретных значенияхполучим функцию, график которой называютинтегральной кривой. Множество таких интегральных кривых называется семейством интегральных кривых. Задавая начальные условия , мы получим уравнениеи отсюда найдем. При этом значениикриваяпроходит через точку.

Пример. Пусть . Выберем ту интегральную кривую, которая проходит через точку. Тогда, и график функциипроходит через заданную точку.

Вопрос о существовании первообразных мы рассмотрим позднее. Далее будет доказано, что любая непрерывная на отрезке функция, имеет на нем первообразную.

П.2 Свойства неопределенных интегралов

Теорема 1. .

Доказательство:

. ■

Теорема 2. .

Доказательство:

. ■

Теорема 3. (с точностью до константы).

Доказательство:

. ■

Теорема 4.

Доказательство:

Для доказательства возьмем производную от обеих частей равенства. ■