
- •Глава VIII Интегральное исчисление функций одного переменного
- •П.1 Понятие первообразной
- •Геометрический смысл неопределенного интеграла
- •П.2 Свойства неопределенных интегралов
- •П.3 Таблица основных интегралов
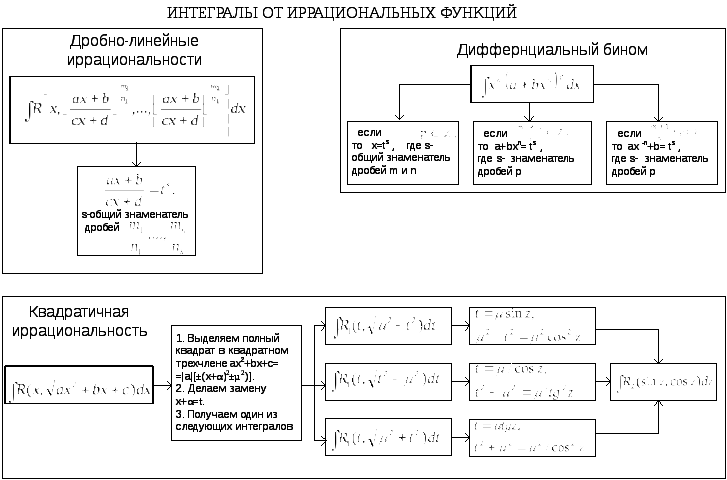
- •П. 4 Общие методы интегрирования
- •2. Интегрирование по частям.
- •3. Интегрирование рациональных дробей.
- •4. Интегрирование тригонометрических функций.
- •5. Интегрирование иррациональных функций.
- •П. 5 Конструкция определенного интеграла
- •П. 6 Суммы Дарбу и их свойства
- •Свойства сумм Дарбу
- •П. 8 Классы интегрируемых функций
- •П. 9 Свойства интегрируемых функций
- •П. 10 Свойства определенного интеграла
- •П 11. Дифференцирование определенного интеграла по верхнему (нижнему) пределу. Формула Ньютона-Лейбница
- •П 12. Замена переменной в определенном интеграле
- •П 13. Интегрирование по частям в определенном интеграле
- •П 14. Вычисление площадей плоских фигур
- •14.1. Вычисление площадей плоских фигур в декартовых координатах
- •14.2. Вычисление площадей плоских фигур в полярных координатах
- •П 15. Вычисление длины кривой
- •П 16. Несобственный интеграл первого рода. Критерий Коши. Признаки сравнения.
- •П 17. Условная сходимость несобственного интеграла. Признак Абеля-Дирихле.
- •§11. Несобственный интеграл и ряд. Интегральный признак Коши сходимости ряда.
- •§12. Несобственный интеграл второго рода.
- •П 18. Главное значение несобственного интеграла.
4. Интегрирование тригонометрических функций.
Алгоритмы вычисления таких интегралов даются в прилагаемых ниже таблицах.
|
| |
|
| |
|
|
|
|
|
|
| |
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
| |
|
Общий случай:
|
5. Интегрирование иррациональных функций.
Алгоритмы вычисления таких интегралов даются в прилагаемых ниже таблицах.
П. 5 Конструкция определенного интеграла
Пусть
функция
![]() определена на отрезке
определена на отрезке![]() .
Разобьем этот отрезок на
.
Разобьем этот отрезок на![]() произвольных частей точками разбиения
произвольных частей точками разбиения![]() .
В каждом из полученных отрезков
.
В каждом из полученных отрезков![]() выберем произвольную точку
выберем произвольную точку![]() .
Через
.
Через![]() обозначим длину отрезка
обозначим длину отрезка![]() .
Обозначим сумму
.
Обозначим сумму![]() ,
которую назовем интегральной суммой
Римана функции
,
которую назовем интегральной суммой
Римана функции![]() на отрезке
на отрезке![]() ,
соответствующей данному разбиению
,
соответствующей данному разбиению![]() отрезка
отрезка![]() и данному выбору точек
и данному выбору точек![]() .
.
Геометрический
смысл интегральной суммы
![]() заключается в том, что это сумма площадей
прямоугольников с основаниями
заключается в том, что это сумма площадей
прямоугольников с основаниями![]() и высотой
и высотой![]() (при выполнении условия
(при выполнении условия![]() ).
).
Обозначим
через
![]() длину наибольшего отрезка разбиения
длину наибольшего отрезка разбиения![]() :
:
![]() .
.
Определение
1. Если
существует конечный предел интегральной
суммы
![]() при
при![]() и при условии, что он не зависит от
разбиения
и при условии, что он не зависит от
разбиения![]() отрезка
отрезка![]() и от выбора точек
и от выбора точек![]() ,
то этот предел называетсяопределенным
интегралом
Римана
от функции
,
то этот предел называетсяопределенным
интегралом
Римана
от функции
![]() на отрезке
на отрезке![]() и обозначается
и обозначается![]() .
.
Другими
словами,
![]() :
:
![]()
![]()
![]()
![]()
![]() .
Нетрудно видеть, что мы дали определение
интеграла Римана в духе определения
предела по Коши.
.
Нетрудно видеть, что мы дали определение
интеграла Римана в духе определения
предела по Коши.
Будет
полезным дать определение
![]() в духе определения предела по Гейне.
в духе определения предела по Гейне.
Определение
2. Функцию
![]() ,
для которой существует предел
,
для которой существует предел
![]() ,
называютинтегрируемой
по Риману.
Множество всех интегрируемых по Риману
на отрезке
,
называютинтегрируемой
по Риману.
Множество всех интегрируемых по Риману
на отрезке
![]() функций обозначают
функций обозначают![]() .
.
П. 6 Суммы Дарбу и их свойства
Определение
1. Пусть
функция f(x)
ограничена на отрезке
![]() ,
иr
– разбиение этого отрезка. Обозначим
через
,
иr
– разбиение этого отрезка. Обозначим
через
![]() ,
,![]() ,
,![]() .
Тогда суммы
.
Тогда суммы![]() и
и![]() называютверхней
и нижней
суммами Дарбу
функции f(x)
для данного
разбиения r
отрезка
называютверхней
и нижней
суммами Дарбу
функции f(x)
для данного
разбиения r
отрезка
![]() .
.
Из
определения ТВГ и ТНГ (![]()
![]()
![]() )
функцииf(x)
следует, что
)
функцииf(x)
следует, что
![]() ,
т.е.
,
т.е.![]() .
.
Геометрический смысл сумм Дарбу
Рассмотрим
неотрицательную непрерывную функцию
f(x)
на отрезке
![]() .
.
![]() - площадь “описанной” ступенчатой
фигуры,
- площадь “описанной” ступенчатой
фигуры,
![]() - “вписанной” ступенчатой фигуры.
Следует отметить, что суммы Дарбу зависят
только от разбиения отрезка
- “вписанной” ступенчатой фигуры.
Следует отметить, что суммы Дарбу зависят
только от разбиения отрезка
![]() ,
в то время как интегральная сумма σ
зависит еще и от выбора точек
,
в то время как интегральная сумма σ
зависит еще и от выбора точек
![]() :
при фиксированном разбиении отрезка
:
при фиксированном разбиении отрезка
![]() суммы
суммы
![]() и
и
![]() - некоторые числа, а суммаσ
– переменная величина, т.к.
- некоторые числа, а суммаσ
– переменная величина, т.к.
![]() произвольны.
произвольны.
Свойства сумм Дарбу
1.
Для любого фиксированного разбиения r
и для любого
![]() точки
точки![]() на отрезках
на отрезках![]() можно выбрать так, что суммаσ
будет удовлетворять неравенству
можно выбрать так, что суммаσ
будет удовлетворять неравенству
![]() .
Точки
.
Точки![]() можно выбрать также и таким образом,
что
можно выбрать также и таким образом,
что![]() .
.
Доказательство:
Пусть
r
– некоторое фиксированное разбиение
отрезка
![]() .
По определению ТВГ для данного
.
По определению ТВГ для данного
![]() на отрезке
на отрезке![]() можно указать такую точку
можно указать такую точку![]() ,
что
,
что![]() .
Умножим неравенство на
.
Умножим неравенство на![]() и просуммируем, получим
и просуммируем, получим![]() .
Аналогично,
.
Аналогично,![]() .
■
.
■
2.
От добавления к данному разбиению r
отрезка
![]() новых точек разбиения нижняя сумма
Дарбу не уменьшается, а верхняя – не
увеличивается.
новых точек разбиения нижняя сумма
Дарбу не уменьшается, а верхняя – не
увеличивается.
Доказательство:
Достаточно
ограничиться добавлением к данному
разбиению r
еще одной точки разбиения
![]() .
Предположим, что точка
.
Предположим, что точка![]() попала в отрезок
попала в отрезок![]() .
Обозначим через
.
Обозначим через
![]() и
и
![]() -
нижние, а через
-
нижние, а через
![]() и
и![]() - верхние суммы Дарбу для данного
разбиенияr
и нового
- верхние суммы Дарбу для данного
разбиенияr
и нового
![]() .
Рассмотрим нижние суммы Дарбу. Обозначим
через
.
Рассмотрим нижние суммы Дарбу. Обозначим
через
![]() и
и
![]() ТВГ функции
ТВГ функции
![]() на отрезках
на отрезках![]() и
и![]() .
В сумму
.
В сумму![]() входит слагаемое
входит слагаемое![]() ,
а в сумму
,
а в сумму![]() вместо него слагаемые
вместо него слагаемые![]() .
Остальные слагаемые в этих суммах
одинаковы. Так как
.
Остальные слагаемые в этих суммах
одинаковы. Так как![]() и
и![]() ,
то
,
то![]()
![]() .
Отсюда получим
.
Отсюда получим
![]() .
Аналогично
.
Аналогично![]() .
■
.
■
3.
Нижняя сумма Дарбу для любого разбиения
![]() не превосходит верхней суммы Дарбу для
любого другого разбиения
не превосходит верхней суммы Дарбу для
любого другого разбиения
![]() .
.
Доказательство:
Пусть
![]() и
и![]() ,
,![]() и
и![]() -
нижняя и верхняя суммы Дарбу соответственно
для разбиений
-
нижняя и верхняя суммы Дарбу соответственно
для разбиений
![]() и
и
![]() .
Рассмотрим разбиение
.
Рассмотрим разбиение
![]() ,
состоящее из точек, входящих в разбиения
,
состоящее из точек, входящих в разбиения
![]() и
и
![]() .
Обозначим его суммы Дарбу
.
Обозначим его суммы Дарбу
![]() и
и![]() .
Так как разбиение
.
Так как разбиение
![]() может быть получено из разбиения
может быть получено из разбиения
![]() добавлением к нему точек разбиения
добавлением к нему точек разбиения
![]() ,
то по свойству 2, учитывая
,
то по свойству 2, учитывая
![]() ,
получим
,
получим![]() .
Но разбиение
.
Но разбиение
![]() может быть получено из
может быть получено из
![]() добавлением точек
добавлением точек
![]() .
Поэтому
.
Поэтому
![]() .
Отсюда
.
Отсюда![]() ,
,![]() .
■
.
■
4.
Множество
![]() верхних сумм Дарбу функции
верхних сумм Дарбу функции![]() для всевозможных разбиений отрезка
для всевозможных разбиений отрезка
![]() ограничено снизу, а множество
ограничено снизу, а множество
![]() нижних сумм Дарбу ограничено сверху,
причем
нижних сумм Дарбу ограничено сверху,
причем![]() .
.
Доказательство:
Это
свойство непосредственно следует из
свойства 3. Действительно, множество
![]() ограничено снизу, а множество
ограничено снизу, а множество![]() ограничено сверху. Поэтому по принципу
ТВГ и ТНГ они имеют точные грани. Обозначим
ограничено сверху. Поэтому по принципу
ТВГ и ТНГ они имеют точные грани. Обозначим![]() ,
,![]() .
Покажем, что
.
Покажем, что![]() .
.
Пусть
![]() .
Тогда положим
.
Тогда положим![]() .
Из свойств точных граней следует, что
существуют числа
.
Из свойств точных граней следует, что
существуют числа![]() и
и![]() (
(![]() - верхняя сумма Дарбу для разбиения
- верхняя сумма Дарбу для разбиения![]() ,
,![]() - нижняя сумма Дарбу для разбиения
- нижняя сумма Дарбу для разбиения![]() )
такие, что
)
такие, что![]() ,
,![]() .
Отсюда получим
.
Отсюда получим![]() .
Но
.
Но![]() ,
поэтому
,
поэтому![]() или
или![]() ,
что противоречит свойству 3. ■
,
что противоречит свойству 3. ■
п. 7 Критерий интегрируемости функций
Теорема
1.
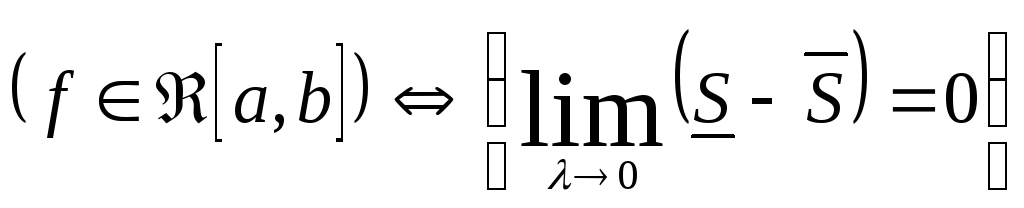 .
.
Доказательство:
Необходимость.
Пусть
![]() ,
т.е. существует
,
т.е. существует![]() .
Это означает, что
.
Это означает, что![]()
![]()
![]() независимо от выбора точек
независимо от выбора точек![]() выполняется неравенство
выполняется неравенство![]() (1). Зафиксируем любое такое разбиение
(1). Зафиксируем любое такое разбиение![]() .
Для него согласно свойству 1 сумм Дарбу
можно указать такие суммы
.
Для него согласно свойству 1 сумм Дарбу
можно указать такие суммы![]() и
и![]() ,
что выполняются неравенства
,
что выполняются неравенства![]() (2) и
(2) и![]() (3). Отметим, что обе суммы
(3). Отметим, что обе суммы![]() и
и![]() удовлетворяют неравенству (1). Из равенства
удовлетворяют неравенству (1). Из равенства![]() и неравенств (1)-(3) следует
и неравенств (1)-(3) следует![]() ,
а это означает
,
а это означает![]()
![]() :
:![]() (так
как
(так
как![]() (4),
следовательно,
(4),
следовательно,![]() )
или
)
или![]() .
.
Достаточность.
Пусть выполнено неравенство (4). Согласно
свойству 4 сумм Дарбу для любых
![]() и
и![]() имеет место неравенство
имеет место неравенство![]() ,
поэтому
,
поэтому![]() .
Отсюда согласно (4) следует, что
.
Отсюда согласно (4) следует, что![]()
![]() .
Значит,
.
Значит,![]() ,
т.е.
,
т.е.![]() .
Полагая
.
Полагая![]() ,
получим, что для любого разбиения
,
получим, что для любого разбиения![]() имеет место неравенство
имеет место неравенство![]() (5). Если же интегральная сумма
(5). Если же интегральная сумма![]() и суммы Дарбу
и суммы Дарбу![]() и
и![]() отвечают одному и тому же разбиению
отвечают одному и тому же разбиению![]() ,
то
,
то![]() (6). Из неравенств (5) и (6) следует, что
(6). Из неравенств (5) и (6) следует, что![]() (7). По условию для любого
(7). По условию для любого![]() существует такое
существует такое![]() ,что
из того, что
,что
из того, что![]() ,
следует
,
следует
![]() .
Тогда из неравенства (7) получим
.
Тогда из неравенства (7) получим
![]() при условии
при условии![]() .
Это означает, что числоI
является
пределом интегральной суммы σ
при
.
Это означает, что числоI
является
пределом интегральной суммы σ
при
![]() ,
т.е.
,
т.е.![]() .
■
.
■
В
дальнейшем нам понадобится другая форма
записи необходимого и достаточного
условия интегрируемости функции. Для
этого введем
![]() - колебание функции
- колебание функции![]() на отрезке
на отрезке![]() .
Тогда
.
Тогда![]()
![]() .
Так как
.
Так как![]() и
и![]() ,
то каждое слагаемое в сумме неотрицательно,
и критерий существования определенного
интеграла можно записать следующим
образом: (
,
то каждое слагаемое в сумме неотрицательно,
и критерий существования определенного
интеграла можно записать следующим
образом: (![]() )
)![]() (
(![]()
![]()
![]()
![]() ).
).











