
- •Глава IV Числовые последовательности
- •Бмп (бесконечно малые последовательности);
- •3. Неограниченные;
- •Пример. Последовательность ограничена, но не является бмп.
- •П. 3 Сходящиеся последовательности
- •П. 4 Арифметические свойства пределов
- •П. 5 Свойства пределов, связанные с неравенствами
- •П. 6 Принцип компактности и принцип полноты
- •Ясно, что можно привести примеры последовательностей, которые расходятся, но их подпоследовательности являются сходящимися.
- •П. 7 Число e
Глава IV Числовые последовательности
п. 1 Определение и примеры
Определение
1. Рассмотрим
множество
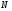 натуральных чисел и множество
натуральных чисел и множество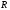 действительных чисел. Если
действительных чисел. Если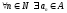 ,
то правило такого соответствия
,
то правило такого соответствия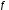 и его результат называетсячисловой
последовательностью
и
обозначается
и его результат называетсячисловой
последовательностью
и
обозначается
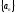 ,
где
,
где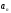 – общий член последовательности.
– общий член последовательности.
Замечание.
Очевидно,
что последовательность – множество
значений функции натурального
аргумента, т.е.
 .
.
Замечание.
Существенно, что в определении
последовательности аргумент
 пробегает все множество
пробегает все множество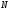 .
.
Замечание. Последовательность конечного числа элементов (конечная последовательность) называют кортежем или вектором. Такие последовательности рассматривать не будем.
Способы задания последовательности
аналитический:
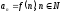 ;
;рекуррентный:
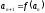 .
.
Арифметическая
прогрессия
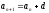 ,
геометрическая прогрессия
,
геометрическая прогрессия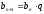 ,
факториал
,
факториал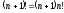 ,
где
,
где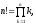 причем
причем ,
- примеры задания последовательностей
рекуррентным способом.
,
- примеры задания последовательностей
рекуррентным способом.
Последовательности бывают:
1. ограниченные;
Бмп (бесконечно малые последовательности);
3. Неограниченные;
4. ББП (бесконечно большие последовательности).
Определение
2. Последовательность
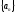 называетсяограниченной,
если существуют такие действительные
числа m
и M
(
называетсяограниченной,
если существуют такие действительные
числа m
и M
(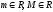 ),
что
),
что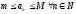 (для
любого натурального числаn).
(для
любого натурального числаn).
Определение
2*. Пусть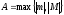 (А
– максимальное из чиселm
и M).
Тогда последовательность
(А
– максимальное из чиселm
и M).
Тогда последовательность
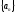 называетсяограниченной,
если
называетсяограниченной,
если
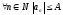 .
.
Пример.
Последовательность
0,1,0,1, ... ограничена, т.к.
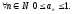
Определение
3.Последовательность
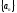 называетсяБМП
(бесконечно
малой последовательностью)
,
если для любого положительного
(эпсилон) найдется номер, зависящий от
,
такой, что, как только n>N
выполняется неравенство
называетсяБМП
(бесконечно
малой последовательностью)
,
если для любого положительного
(эпсилон) найдется номер, зависящий от
,
такой, что, как только n>N
выполняется неравенство
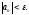
(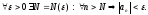 )
)
Пример.
Рассмотрим последовательность
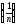 .
Для того, чтобы
.
Для того, чтобы
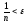 необходимо, чтобы
необходимо, чтобы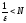 ,
т.е.
,
т.е. (
(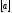 – целая часть числа
– целая часть числа ).
Задавая
).
Задавая некоторые значения, будем получать
номер
некоторые значения, будем получать
номер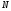 ,
начиная с которого члены последовательности
,
начиная с которого члены последовательности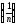 попадут в
попадут в -коридор.
Например, если
-коридор.
Например, если =10,
то
=10,
то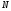 =0,
тогда
=0,
тогда =1;
если
=1;
если =1,
то
=1,
то =1,
тогда
=1,
тогда =2;
если
=2;
если =0,1,
то
=0,1,
то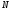 =10,
тогда
=10,
тогда =11,
и т.д.
=11,
и т.д.
Замечание. Обычно БМП обозначают первыми буквами алфавита.
Пример. Последовательность ограничена, но не является бмп.
Определение
4. Последовательность
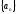 называетсянеограниченной,
если
называетсянеограниченной,
если
для
любого неотрицательного числа А
найдется n,
такой что
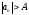 .
.
(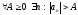 .)
.)
Определение
5. Последовательность
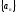 называетсяББП,
если для любого положительного М
найдется
номер, зависящий от М,
такой, что, как только n>N
выполняется неравенство
называетсяББП,
если для любого положительного М
найдется
номер, зависящий от М,
такой, что, как только n>N
выполняется неравенство
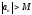 (
(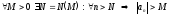 ).
).
Пример.
Последовательность
 является ББП, а последовательность
является ББП, а последовательность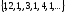 является неограниченной, но не является
ББП.
является неограниченной, но не является
ББП.
п. 2 Свойства БМП
Вспомним
определение БМП: если для любого
положительного
(эпсилон)
найдется номер, зависящий от ,
такой, что, как только n>N
выполняется неравенство
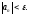
(*)
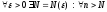
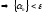 ,
то
,
то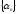 -
БМП.
-
БМП.
Теорема 1. Сумма двух БМП есть БМП.
Доказательство:
Пусть
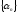 и
и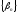 - БМП. Тогда соотношение (*) имеет место
для каждой из данных последовательностей.
Выберем
- БМП. Тогда соотношение (*) имеет место
для каждой из данных последовательностей.
Выберем ,
тогда для последовательности
,
тогда для последовательности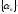 найдется номер
найдется номер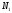 ,
начиная с которого
,
начиная с которого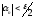 ,
а для последовательности
,
а для последовательности найдется номер
найдется номер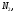 начиная с которого
начиная с которого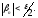

Рассмотрим
последовательность
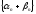 .
Пусть
.
Пусть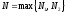 тогда, начиная с номера
тогда, начиная с номера ,
,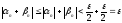 ,
т.е. для
,
т.е. для ,
начиная с номера
,
начиная с номера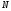
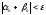 .
Это означает, что последовательность
.
Это означает, что последовательность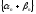 является БМП.
является БМП.
Следствие. Сумма любого конечного числа БМП есть БМП. (Доказать самостоятельно).
Теорема 2. БМП ограничена.
Доказательство:
Пусть
 - БМП. Тогда для нее имеет место соотношение
(*), т.е. начиная с некоторого
- БМП. Тогда для нее имеет место соотношение
(*), т.е. начиная с некоторого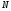 члены
члены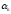 войдут в
войдут в -коридор.
Другими словами, из этого
-коридор.
Другими словами, из этого -коридора
выпадает не более чем конечное число
первых членов последовательно-
-коридора
выпадает не более чем конечное число
первых членов последовательно-
сти
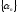 .
Пусть
.
Пусть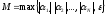 ,
тогда
,
тогда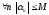 ,
что означает ограниченность
последовательности
,
что означает ограниченность
последовательности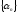 .
.
Теорема
3.
Если
 - БМП, а
- БМП, а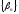 ограничена, то последовательность
ограничена, то последовательность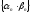 является БМП.
является БМП.
Доказательство:
Так
как
 -БМП,
то имеет место соотношение (*). Выберем
-БМП,
то имеет место соотношение (*). Выберем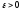 и найдем номер
и найдем номер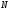 ,
начиная с которого члены последовательности
,
начиная с которого члены последовательности войдут в
войдут в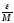 -коридор,
где число
-коридор,
где число .
Тогда, начиная с номера
.
Тогда, начиная с номера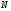 ,
будет выполняться неравенство
,
будет выполняться неравенство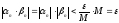 .
.
Следствие 1. Произведение двух БМП есть БМП. (Доказать самостоятельно).
Следствие 2. Произведение любого конечного БМП есть БМП. (Доказать самостоятельно).
Теорема
4.
Для
того, чтобы последовательность
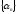 была БМП, необходимо и достаточно, чтобы
была БМП, необходимо и достаточно, чтобы была ББП.
была ББП.
Доказательство:
Необходимость.
Пусть
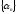 - ББП. Тогда имеет место соотношение
(*), т.е., начиная с некоторого номера
- ББП. Тогда имеет место соотношение
(*), т.е., начиная с некоторого номера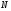
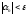 .
Пусть
.
Пусть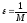 ,
тогда
,
тогда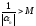 ,
т.е.
,
т.е. ,
что означает:
,
что означает: - ББП.
- ББП.
Достаточность доказать самостоятельно.
