
- •Глава IV Числовые последовательности
- •Бмп (бесконечно малые последовательности);
- •3. Неограниченные;
- •Пример. Последовательность ограничена, но не является бмп.
- •П. 3 Сходящиеся последовательности
- •П. 4 Арифметические свойства пределов
- •П. 5 Свойства пределов, связанные с неравенствами
- •П. 6 Принцип компактности и принцип полноты
- •Ясно, что можно привести примеры последовательностей, которые расходятся, но их подпоследовательности являются сходящимися.
- •П. 7 Число e
П. 4 Арифметические свойства пределов
Теорема
1.
Пусть
последовательности
 и
и сходятся, тогда сходится и последовательность
сходятся, тогда сходится и последовательность ,
причем
,
причем .
.
Доказательство:
Так
как
 и
и ,
то
,
то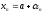 ,
, ,
где
,
где и
и - БМП. Рассмотрим
- БМП. Рассмотрим ,
причем
,
причем - БМП. Следовательно,
- БМП. Следовательно, .
.
Следствие. Сумма любого конечного числа сходящихся последовательностей, является сходящейся последовательностью, предел которой равен сумме соответствующих пределов.
Теорема
2.
Если
 ,
,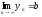 (пределы
последовательностейxп
и
yп
равны a
и b
соответственно), то
(пределы
последовательностейxп
и
yп
равны a
и b
соответственно), то
 .
.
Доказательство:
В
силу определения предела последователь-
ности имеем

 где
где ,
, - БМП. Рассмотрим
- БМП. Рассмотрим
 ,
при этом
,
при этом - БМП. Следовательно,
- БМП. Следовательно,
Теорема
3.
Если
пределы последовательностей xп
и
yп
равны a
и b
соответственно для любого натурального
числа n
и yп
≠0,
b≠0
( ,
,
 ),
то
),
то .
.
Доказательство:
Докажем сначала лемму.
Лемма.
Если последовательность
 сходится
сходится ,
то последовательность
,
то последовательность - ограничена.
- ограничена.
Пусть
 .
Тогда имеет место соотношение (**). Пусть
в (**)
.
Тогда имеет место соотношение (**). Пусть
в (**) т.е.
т.е. .
Тогда существует номер
.
Тогда существует номер ,
начиная с которого
,
начиная с которого или
или .
Следовательно,
.
Следовательно, или
или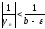 .
Пусть
.
Пусть .
Тогда
.
Тогда .
▲
.
▲
Рассмотрим

 .
Так как
.
Так как - БМП, а
- БМП, а - ограничена, то
- ограничена, то - БМП. Таким образом,
- БМП. Таким образом, .
.
П. 5 Свойства пределов, связанные с неравенствами
Теорема
1. Пусть
 .
Тогда, если найдется номер
.
Тогда, если найдется номер ,
начиная с которого
,
начиная с которого ,
то
,
то .
.
Доказательство:
Так
как
 ,
то для нее имеет место соотношение (**).
Предположим противное, т.е. пусть
,
то для нее имеет место соотношение (**).
Предположим противное, т.е. пусть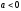 .
Тогда из соотношения (**) имеем
.
Тогда из соотношения (**) имеем .
Так как
.
Так как ,
то можно выбрать такое
,
то можно выбрать такое ,
что
,
что и
и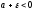 .
Тогда, начиная с некоторого номера,
определяемого этим
.
Тогда, начиная с некоторого номера,
определяемого этим ,
, ,
что противоречит условию.
,
что противоречит условию.
Следствие
1.
Пусть
 и существует такой номер
и существует такой номер ,
начиная с которого
,
начиная с которого .
Тогда
.
Тогда .
.
Доказательство:
Рассмотрим
 .
Последовательность
.
Последовательность сходится. Более того, начиная с некоторого
номера
сходится. Более того, начиная с некоторого
номера
 .
Тогда
.
Тогда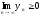 .
Но
.
Но .
Следовательно,
.
Следовательно, .
.
Следствие
2. Пусть
 и, начиная с некоторого номера
и, начиная с некоторого номера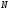 ,
, .
Тогда
.
Тогда .
.
Следствие
3.
Пусть
 и, начиная с некоторого номера
и, начиная с некоторого номера ,
, .
Тогда
.
Тогда .
.
Теорема
2. Пусть
 ,
причем
,
причем .
Тогда существует такой номер
.
Тогда существует такой номер ,
что
,
что .
.
Доказательство:
Так
как
 ,
то имеет место соотношение (**), т.е.
,
то имеет место соотношение (**), т.е. .
Имеем
.
Имеем ,
выберем
,
выберем таким, чтобы
таким, чтобы .
Тогда найдет такой номер
.
Тогда найдет такой номер ,
начиная с которого,
,
начиная с которого, .
.
Следствие
1.
Пусть
 ,
причем
,
причем .
Тогда существует такой номер
.
Тогда существует такой номер ,
начиная с которого,
,
начиная с которого, .
.
Следствие
2.
Пусть
 ,
причем
,
причем .
Тогда существует такой номер
.
Тогда существует такой номер ,
начиная с которого,
,
начиная с которого, .
.
Следствие
3.
Пусть
 ,
причем
,
причем .
Тогда существует такой номер
.
Тогда существует такой номер ,
начиная с которого,
,
начиная с которого, .
.
Теорема
3. Теорема о двух полицаях. Пусть
 ,
, ,
причем начиная с некоторого номера
,
причем начиная с некоторого номера ,
, .
Тогда
.
Тогда .
.
Доказательство:
Так
как последовательности
 и
и сходятся, то имеет место соотношение
(**), т.е.
сходятся, то имеет место соотношение
(**), т.е. и
и .
Пусть
.
Пусть .
Тогда начиная с номера
.
Тогда начиная с номера .
Отсюда получим
.
Отсюда получим ,
или
,
или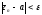 ,
т.е.
,
т.е. .
.
П. 6 Принцип компактности и принцип полноты
Определение
1. Пусть
 - некоторая последовательность. Рассмотрим
последовательность
- некоторая последовательность. Рассмотрим
последовательность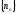 натуральных чисел такую, что
натуральных чисел такую, что .
Тогда последовательность
.
Тогда последовательность называютподпоследовательностью
последовательности
называютподпоследовательностью
последовательности
 .
Если последовательность
.
Если последовательность сходится, то ее предел называютчастичным
пределом
последовательности
сходится, то ее предел называютчастичным
пределом
последовательности
 .
.
Пример.
Рассмотрим последовательность
 .
Тогда
.
Тогда является подпоследовательностью
последовательности
является подпоследовательностью
последовательности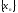 .
.
Теорема
1.
Если
последовательность
 сходится к
сходится к ,
то любая ее подпоследовательность
,
то любая ее подпоследовательность сходится к
сходится к .
.
Доказательство:
Пусть
 ,
тогда имеет место соотношение (**), т.е.
начиная с некоторого номера
,
тогда имеет место соотношение (**), т.е.
начиная с некоторого номера .
Так как члены подпоследовательно-
.
Так как члены подпоследовательно-
сти
 являются членами последовательности
являются членами последовательности ,
то при
,
то при имеем
имеем .
Следовательно,
.
Следовательно, .
.
