П. 3 Сходящиеся последовательности

Определение 1. Последовательность 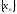называетсясходящейся, если , где- БМП, а число. Тогда числоназываетсяпределом последовательности . Обозначается(при, стремящимся к бесконечности, стремится к (или равно)).

Определение 1*. Последовательность сходится к, т.е.если если для любого положительного (эпсилон) найдется номер, зависящий от , такой, что, как только n>N выполняется соотношение :

(**) .

Покажем, что определения 1и 1* эквивалентны.

Пусть в смысле определения 6. Тогда, где- БМП. Следовательно,- БМП, тогда выполняется соотношение (*), т.е.. Получим соотношение (**).

Теперь пусть в смысле определения 6*. Тогда выполняется соотношение (**). Полагая, получим, которая является БМП в соответствие с соотношением (*). Тогда.

Другой подход: Окрестностью точки называется какой-либо интервал , содержащий эту точку. Символически обозначается.

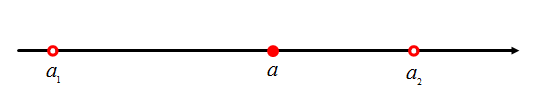
Интервал называется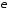-окрестностью точки и символически обозначается.

Есл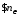и , что приили, т.е. при.

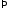
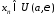Число называетсяпределом числовой последовательности, если, для любого ,- окрестность точкисодержит бесконечное множество элементов числовой последовательности, а вне окрестности – конечное число элементов.

П р и м е р.1. Доказать, что для предел равен нулю.

Очевидно для любого существует, что при

откуда , т.е.и.

Теорема 1. О единственности предела Если последовательность сходится, то она имеет единственный предел.

Доказательство: . Пусть последовательность имеет два предела, т.е.,,для определенности. Так както имеет место соотношение (**), т.е. начиная с некоторого номера. Так както выполняется (**), т.е. начиная с некоторого номера. Пустьтогда, начиная с номера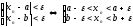. ПустьТогда пересечение этих двух множеств, задаваемых неравенствами, пусто, т.е. нашлось, по крайней мере, однодля которого не выполняется (**). Это означает, что предела не существует.

Комментарий. Предположим, что числовая последовательность имеет два пределаи

,

Построим непересекающиеся - окрестности

Пусть предел равен , тогда- окрестность точкибудет содержать все элементы последовательности, начиная с некоторого номера. Вне этой окрестности будет находиться конечное число элементов, поэтому точкане может быть пределом последовательности, т.е. предел единственный.

Теорема 2. (Вейерштрасса - необходимое условие сходимости) Если последовательность сходится, то она ограничена.

Доказательство:

Пусть последовательность сходится, тогда имеет место соотношение (**), т.е. начиная с некоторого номера,. Положим, тогда. Рассмотрим,т.е.,что озна- чает ограниченность последовательности.

Теорема 3. Признак Больцано-Вейерштрасса.

Если последовательность монотонно возрастает (убывает) и ограничена сверху(снизу), то она сходится.

Доказательство:

Пусть последовательность монотонно возрастает () и ограничена (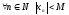). Тогда из условия ограниченности следует, что- непустое ограниченное сверху множество. Следовательно, по теореме о ТВГ (главаIII, п. 4) множество , значит, и последовательность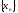имеет ТВГ.

Обозначим и покажем, что.

В силу определения ТВГ имеем . Кроме того, последова- тельностьмонотонно возрастает, поэтому найдется такой номер, чтот.е.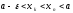. Следовательно,или. Таким образом, существует такой номер, начиная с которого.

Пример. Последовательность монотонно возрастает, но не ограничена, следовательно,расходится.

Пример. Последовательность ограничена, но не является монотонной, следовательно, расходится.

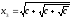Пример. Пусть и,... или(*). Последовательностьмонотонно возрастает и ограничена сверху, например, числом. Покажем это ММИ.

Пусть . Тогда. Тогда существует. Возведем (*) в квадрат и перейдем к пределу при:, т.е.. Таким образом,.