14.2. Вычисление площадей плоских фигур в полярных координатах

Пусть положение любой точки на плоскости однозначно определяется двумя числами , где.

Пусть неотрицательная, непрерывная на отрезкефункция,.

Рассмотрим множество точек

,

которое можно истолковать как криволинейный треугольник

Для вычисления площади криволинейного треугольника разобьём этот треугольник на элементарные криволинейные треугольники.

Элементарные криволинейные треугольники заменим прямоугольными треугольниками.

Высоты этих треугольников положим равными ,

а основания соответственно – .

Площадь -го элементарного треугольник очевидно будет равна

.

Площадь криволинейного треугольника будет приближённо равна

. (1)

Выражение (1) можно рассматривать как интегральную сумму для функции на отрезке.

Введём обозначение .– это мелкость

разбиения .

Тогда площадь криволинейного треугольника

получим при переходе в выражении (1) к пределу при

=. (2)

Итак, площадь плоской фигуры в полярной системе координат равна

.

П р и м е р. Вычислите площадь фигуры, ограниченной кривой (кардиоидой)

.

Р е ш е н и е. Изобразим график кардиоиды

Как видим, кардиоида представляет собой линию, симметричную относительно оси .

Поэтому

П 15. Вычисление длины кривой

Пусть кривая задана параметрически

, .

Разобьем отрезок начастей точками.

Обозначим через соответствующие точки на кривой. Соединим эти точки прямыми.

Полученную при этом ломанную называют ломанной, вписанной в кривую.

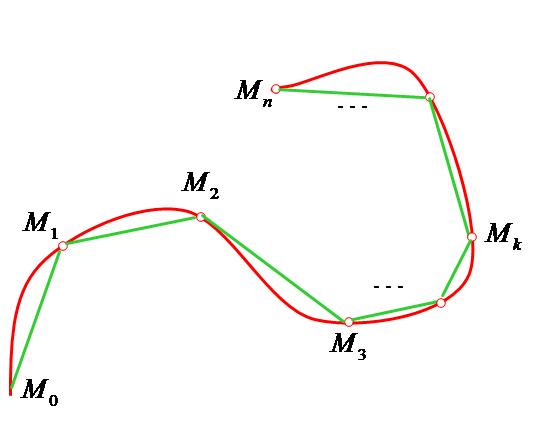
Длину элементарного звена равна

Длина ломанной в таком случае будет равна

. (1)

Обозначим через . Тогда длину кривойполучим, перейдя в выражении (1) к пределу при

. (2)

Итак, длина кривой согласно выражению (2) определяется формулой

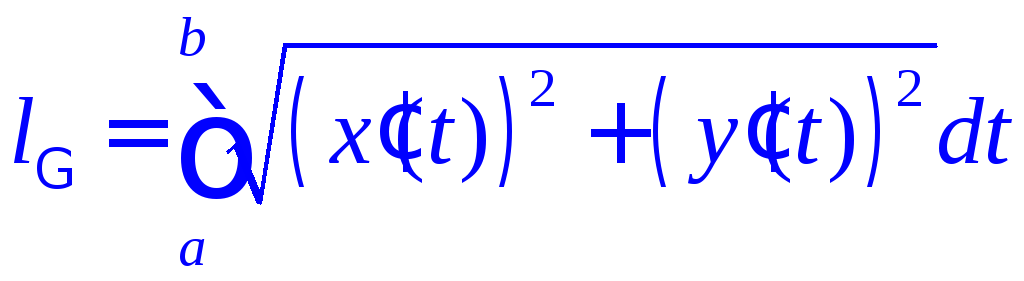. (3)

Длина пространственной кривой , заданной параметрически

, ,

будет равна

.

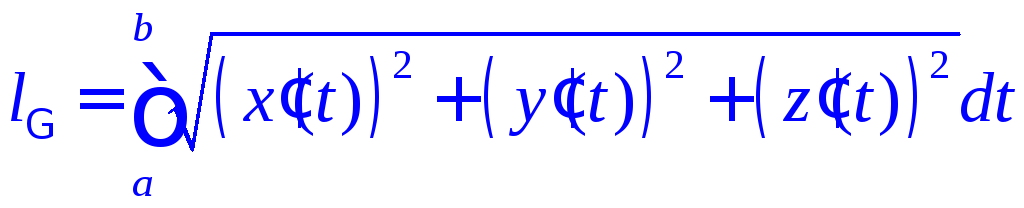Если плоская кривая задана в явном виде

, ,

то параметрические уравнения кривой

можно в этом случае представить в виде

, ,.

В результате выражении (3) получается в виде

.

П р и м е р. Найти длину кривой, заданной параметрически.

Р е ш е н и е. Построим график заданной кривой

Так как кривая симметрична относительно координатных осей, то достаточно найти .

Поэтому длина кривой будет равна

.

П 16. Несобственный интеграл первого рода. Критерий Коши. Признаки сравнения.

Введённое ранее определение интеграла Римана непригодно, если функция f(x) неограниченна на отрезке [a, b] или промежуток интегрирования бесконечен. В этих случаях понятие определённого интеграла можно обобщить и ввести понятие несобственного интеграла.

Пусть функция f(x) определена на бесконечном полуинтервале [a, +∞) и пусть интеграл Римана существует на любом конечном отрезке [a, x] Vx≥a. Тогда имеем функцию F(x), определённую интегралом

(1)

с переменным верхним пределом.

Перейдём в (1) к пределу при x→+∞ и введём формально следующее обозначение

F(x)= (2)

Символ называют несобственным интегралом первого рода. При этом, если предел (2) существует, то несобственный интеграл называется сходящимся. Если предел не существует или равен ∞, то несобственный интеграл называют расходящимся.

Аналогично определяют несобственные интегралы первого рода на (-∞, b] и

(-∞, +∞).

, (3)

Заметим, что в (3) a и b стремятся к бесконечности независимо друг от друга.

Отметим также, что если функция f(x) непрерывна на [a, ∞), то (1) определяет одну из первообразных функций f(x), и при её нахождении можно использовать все методы интегрирования – замену переменных, интегрирование по частям и прочее.

Пример 1. Исследовать на сходимость несобственный интеграл ,a>0.

Решение.

Пусть α=1. Тогда =ln|t|=∞, т.е. интеграл расходится.

Пусть α≠1. Тогда ==()=(-)=

=

Вывод: данный интеграл сходится при α>1 и расходится при α≤1.

Пример 2. Исследовать на сходимость интеграл .

Решение. ==-.

Очевидно, этот предел не существует. Интеграл расходится.

Пример 3. Вычислить интеграл .

Решение.

===()=--()=0+1=1.

Кратко решение записывают так:

=--=0+1=1.

Теорема 1.(критерий Коши).

Для сходимости несобственного интеграла необходимо и достаточно, чтобы дляVε>0 существовало такое A(ε)>0, что для всех x’ и x” больших A(ε) выполнялось неравенство <ε.(4).

Док-во.Согласно критерию Коши функция F(x) имеет предел при x→+∞ только в том случае, когда для Vε>0 существует A(ε)>0 такое, что для Vx’, x”> A(ε) выполняется неравенство

. (5)

Пусть функция F(x) определяется формулой (1). Тогда (см. рис.)

=+=>

=. Отсюда ясно, что условие (5) совпадает с (4). Теорема доказанна.

Теорема 2.(признак сравнения). Пусть f(x)≥0, g(x)≥0 и f(x)≤g(x) и для Vx≥a. Тогда из расходимости интеграла следует расходимость интеграла, а из сходимости интеграласледует сходимость интеграла, причём

≤. (6)

Док-во.Т.к. неравенство можно интегрировать, то из неравенства f(x)≤g(x) имеем ≤дляVx≥a. (7). Поскольку f(x)≥0, то расходимость интеграла означает, что предел левой части неравенства (7) равен +∞. Тогда предел правой части этого неравенства не может быть конечным, т.е. расходится. Первая часть теоремы доказана.

Пусть сходится. Тогда согласно критерию Коши и неравенству (7) имеем

≤<ε. Это означает, что интеграл сходится. Если оба интеграла сходятся, то переходя к пределу в (7), получим (6).

Теорема доказанна.

Теорема 3. (предельный признак сравнения). Если подынтегральные функции интеграловиположительные и существует предел=C>0, то оба интеграла ведут себя одинаково, т.е. сходятся или расходятся одновременно.

Док-во.Из существования предела =C следует, что для Vε>0 существует A(ε)>a такое, что дляVx>A(ε). Перепишем это неравенство в виде С-ε<<C+ε => (C-ε)g(x)<f(x)<(C+ε)g(x). (8)

Если интеграл сходится, то сходится интеграл. Тогда из правой части (8) и теоремы 2 следует сходимость интеграла, следовательно и интеграла. Первая часть теоремы доказана.

Пусть интеграл расходится, следовательно расходится и интеграл. Тогда из левой части (8) и теоремы 2 следует расходимость интеграла, следовательно и интеграла. Теорема доказанна.

Пример 4. Исследовать на сходимость интеграл .

Решение. Поскольку ~приx→+∞, то согласно теореме 3 данный интеграл сходится, т.е. сходится интеграл (см. пр.1).

Пример 5. Исследовать на сходимость интеграл .

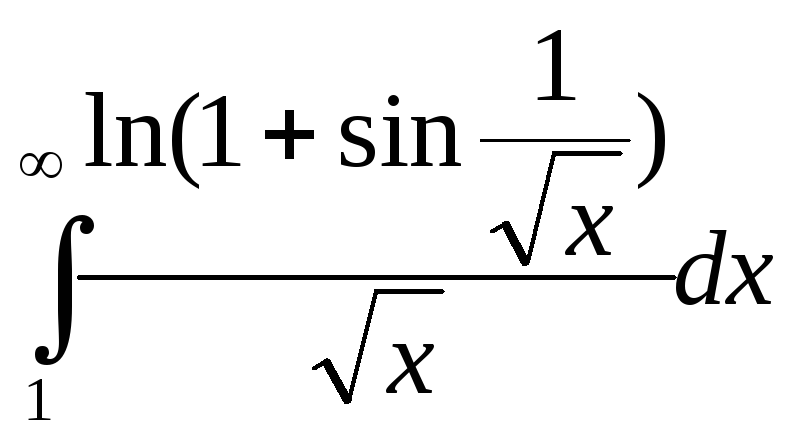Решение. ~~=.

Вывод: интеграл расходится.