Свойства функций

Функцию можно задать тремя способами: аналитически (формулой), графически и таблицей. Например:

1. y=3x⁵+5x³–199x–2001, x(–; +), y(–; +);

2. , x[5; +), y[0; +);

3. 

4. .

В первых двух примерах указаны области D и E. Если какая-либо из них (пример 3) или обе (пример 4) не указаны, считается «по умолчанию», что функция определена в области ее существования. Графический способ продемонстрирован на рис. 2.

Далеко не каждая формула может определять функцию. Например, формула y=lglgsinx не имеет смысла (покажите это!). Поэтому первое, чем следует поинтересоваться при исследовании функций,– область их определения. Множество же значений, даже для очень простой на первый взгляд функции, может оказаться очень сложным, поэтому обычно интересуются, ограничено это множество или нет.

Определение. Функция f(x) называется ограниченной, если xDM>0: |f(x)|M. Это читается так: для любого x, принадлежащего области определения функции, найдется действительное положительное число М, такое, что |f(x)|M, т.е. –Mf(x)M.

Задания. 1. Дайте определение функции, ограниченной сверху (снизу).

2. Дайте определение неограниченной функции.

3. Покажите, что если f(x) и g(x) ограничены хD, то f(x)g(x), f(x)g(x), |f(x)| тоже ограничены на множестве D.

4. Покажите, что модуль и квадрат любой функции есть функция, ограниченная снизу.

Следующим, очень важным свойством функций является их симметричность, т.е. четность-нечетность и периодичность-непериодичность.

Определение.  f(x) задана на симметричном интервале, т.е. хD(–х)D. Тогда, если f(–x)–f(x), то f(x) – нечетная, а если f(–x)≡f(x), то f(x) – четная.

Остальные функции называются функциями общего вида. Их подавляющее большинство, но имеет место такое утверждение:

 f(x): хD(–х)D, т.е. функция задана на симметричном интервале.

Тогда ее можно представить в виде суммы четной и нечетной функций.

;

 .

Исследуем функции (х) и (х) на четность:

;

,

т.е. (х) – функция четная, (х)– нечетная.

Умение «разбить» функцию на четную и нечетную составляющие иногда сильно облегчает ее исследование и построение.

Примеры. 1. y=x², x[–1; 5].

Несмотря на то, что (–х)²=х², эта функция не является четной, так как она задана не на симметричном интервале.

2. ;

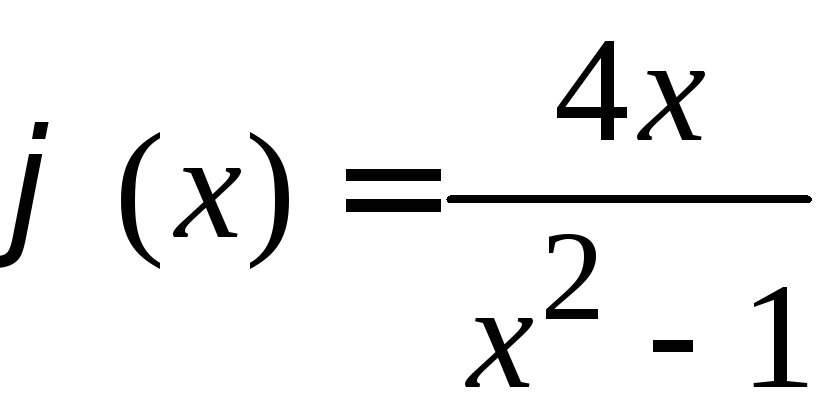. , т.е..

Задания. 1. Продолжить функцию y=f(x): четным образом и нечетным образом (см. рисунок).

2. Представить функции ,y=x³–5x, y=x³+3x+5x–7 в виде суммы четных и нечетных компонент.

3. Доказать, что произведение двух четных функций и двух нечетных функций есть функция четная, а произведение четной функции на нечетную есть функция нечетная.

Определение. Функция f(x) называется периодической с периодом Т, если хD Т>0: 1) хТD; 2) f(x+T)f(x).

Наименьшее значениеТ, если оно существует, называется основным периодом.

Пример. Легко убедиться, что функция y=c периодическая, но не имеет основного периода. При исследовании на периодичность обычно требуется либо найти основной период, либо доказать, что его нет. Рассмотрим характерные примеры решения таких задач.

Пример. Доказать, что функция не является периодической.

Функция f(x) не является периодической, если  хD: Т>0 не будет выполнено хоть одно из условий периодичности. Для заданной функции D: х0. Легко видеть, что если положить х=0, то х+ТD, а х–ТD, .

Пример. Доказать непериодичность функции y=3x²+5x+7.

y=3x²+5x+7– периодическая функция. Тогда при всех прочих условиях будет выполнено тождество f(x+T)f(x), т.е. 3(х+Т)²+5(х+Т)+7=3х²+5х+7, Т=0 или , но этого не может быть, так какТ– положительная константа.

Пример. Найти основной период функций:

а) y=3sinx+sin2x; б) y=3cosx+cos2x.

а)  Т>0– период, тогда 3sin(x+T)+sin2(x+T)=3sinx+sin2X.  х=0.

Тогда 3sinT+2sinTcosT=0  Так как |cosT|1, то 3+2cosT0, следовательно, sinT=0, T=k, kN (почему N, а не Z?)

Выполняя проверку убеждаемся, что T= не является периодом при k=1.

 , тогда 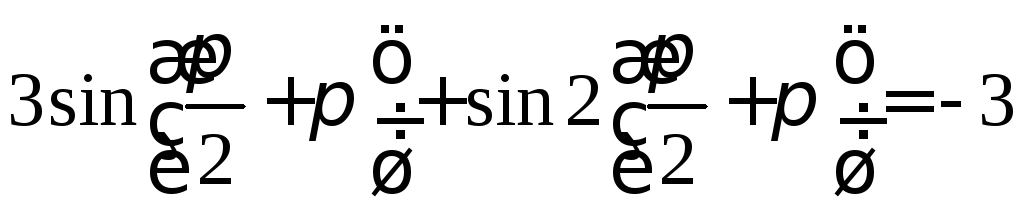(в данном случае можно воспользоваться формулами приведения). k=2, T=2. Легко заметить, что Т=2 – наименьший период.

б)  T>0 – период функции y=cosx+cos2x.

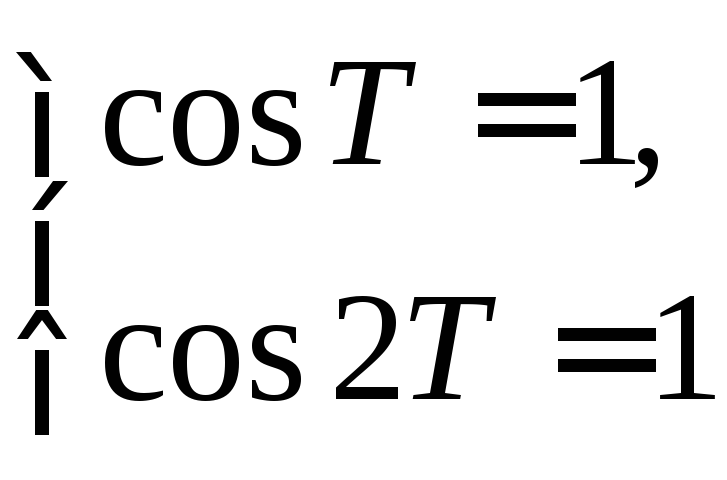
Аналогично хD должно выполняться равенство 3cos(x+T)+cos2(x+T)= =3cosx+cos2X.  х=0, тогда 3cosT+cos2T=4. Так как |cosT|1, |cos2T|1, то  k, lN. Наименьшее положительное значение Т, удовлетворяющее системе, есть Т=2.

Другой способ нахождения основного периода связан с преобразованием изменения масштаба (см. дальше п. 3.1). Если периодическая функция f(x) имеет период T_осн, то период функции f( x) равен .

Пример. Найти основной период функции .

Так как T_осн для sinx и для cosx равен 2, то ;.

Основной период суммы этих двух функций , т.е. 10k=21l, т.е. k=21, если l=10, следовательно, илиT=7 10=70.