3. Функция

1. Если переменная y пропорциональна переменной x, то эта зависимость выражается формулой  y=kx, где k0 – коэффициент пропорциональности.

2. Если переменная y обратно пропорциональна переменной x, то эта зависимость выражается формулой , гдеk0 – коэффициент обратной пропорциональности.

3. Область определения функции есть множество всех чисел, отличных от нуля, т.е..

4. Графиком обратной пропорциональности является кривая, состоящая из двух ветвей, симметричных относительно начала координат. Такая кривая называется гиперболой (рис. 14).

Если k>0, то ветви гиперболы расположены в I и III координатных четвертях; если же k<0, – то во II и IV координатных четвертях.

4. Дробно-линейная функция

1. Функция вида , гдеa, b, c, d – постоянные, причем c0 (иначе мы имели бы линейную функцию) и adbc (иначе получили бы функцию вида y=const), называется дробно-линейной. Функция определена всюду, кроме точки .

2. Для построения графика преобразуем правую часть равенства, выделив целую часть:

.

Полагая ,,, получаем, что дробно-линейную функцию всегда можно привести к виду.

3. График функции можно получить, сдвигая гиперболуна |m| единиц вдоль оси ox и на |n| единиц вдоль оси oy. В каком направлении выполняется сдвиг, зависит от знаков m и n (рис.15).

При этом сдвиге асимптоты гиперболы(координатные оси) перейдут в прямые,.

Эти прямые будут асимптотами графика дробно-линейной функции.

Пример. Построить график функции .

Выделим целую часть функции:

. Отсюда следует, что прямые x=1,5 и y=2 являются асимптотами данной функции.

Теперь находим точки ее пересечения с осямиox и oy. При x=0 . Еслиy=0, то , т.е..

Следовательно, гипербола пересекает ось ox в точке , а осьoy – в точке . Взяв еще несколько контрольных точек, построим график (гиперболу) (рис.16).

Замечание. В отличие от графика функции график дробно-линейнойфункции может пересекать оси координат.

5. Степенная функция y=x^a

Здесь a – любое действительное число. В общем случае степенная функция определена при x>0; она монотонно возрастает, если a>0, и монотонно убывает, если a<0 (рис. 17, 18).

Частные случаи:

1. если a – целое положительное число, то функция y=x^a определена на всей вещественной оси –<x<+. Графики степенной функции при a=3 и a=4 изображены на рис. 19 и 20;

2. если a – целое отрицательное число, то функция x^a определена при всех значениях x, кроме x=0 (рис. 21 и 22).

3. если – рациональное число, гдеq – нечетное число, то функция x^a определена на всей вещественной оси, а при четном q функция x^a определена для x0.

6. Показательная функция y=a^x (a>0, a≠1)

Область определения – вся числовая прямая R. Число a называется основанием степени. При a>1 показательная функция монотонно возрастает, а при 0<a<1 – монотонно убывает (рис. 23).

7. Логарифмическая функция y=log_ax (a>1, a≠1)

Числоa называется основанием логарифмической функции. Область определения – бесконечный промежуток (0, +). При a>1 логарифмическая функция монотонно возрастает, а при 0<a<1 – монотонно убывает (рис. 24).

Логарифмическая функция y=log_ax является обратной функцией для показательной функции y=a^x. Логарифмическую функцию с основанием a=e обозначают lnx и называют натуральным логарифмом, а логарифмическую функцию с основанием a=10 обозначают lgx и называют десятичным логарифмом, т.е. log_ex=lnx, log₁₀x=lgx.

8. Тригонометрическая функция y=sinx

Функция определена для всехx, она периодическая с периодом T=2. График синуса называют синусоидой (рис. 25).

9. Тригонометрическая функция y=cosx

Функция определена для всех x, ее период T=2, график изображен на рис. 26. График функции y=cosx получается из графика y=sin x смещением его вдоль оси ox влево на отрезок .

10. Тригонометрическая функция y=tgx

Функция определена всюду, кроме точек . Она периодическая с периодомT=. График функции изображен на рис. 27.

11. Тригонометрическая функция y=ctgx

Функция определена всюду, кроме точек x=k (k=0, ±1, ±2, …). Функция периодическая, T= (рис. 28).

12. Тригонометрические функции y=secx, y=cosecx

Функции секанс и косеканс определяются соответственно равенствами

, ;

они определены всюду, кроме точек, в которых знаменатели обращаются в нуль (см. п. 3.5).

13. Обратная тригонометрическая функция y=arcsinx

Рассмотрим функцию y=sinx на отрезке . На этом отрезке функцияy=sinx монотонно возрастает. Значит, она имеет обратную функцию x=arcsiny, которая определена на отрезке [–1, 1], а область ее значений – отрезок . График функцииy=arcsinx изображен на рис. 29.

14. Обратная тригонометрическая функция y=arccosx

Рассмотрим функциюy=cosx на отрезке [0, ]. На отрезке [0, ] функция y=cosx монотонно убывает, так что она имеет обратную функцию x=arccosy, которая определена на отрезке [–1, 1], а ее значения заполняют отрезок [0, ]. График функции y=arccosx изображен на рис. 30.

15. Обратная тригонометрическая функция y=arctgx

Рассмотрим функцию y=tgx на интервале . При этих значенияхx функция tgx монотонно возрастающая и ее значения заполняют интервал (–, +). Следовательно, функция y=tgx имеет обратную, которая обозначается x=arctgy. Она определена на всей числовой оси, а ее значения заполняют интервал 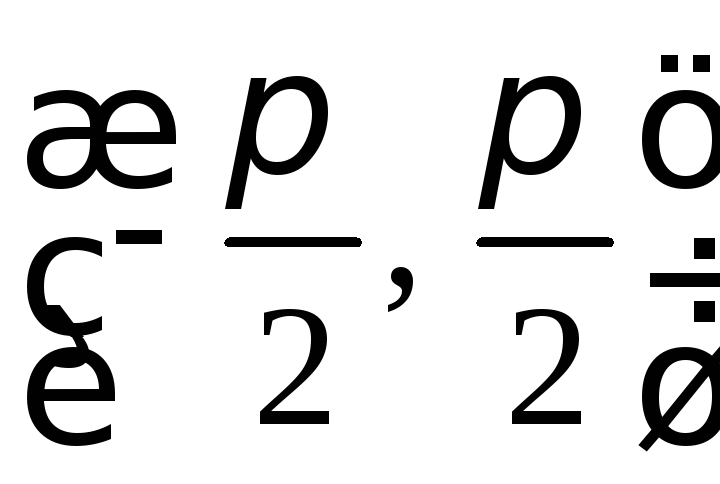. График функцииy=arctgx представлен на рис. 31.

1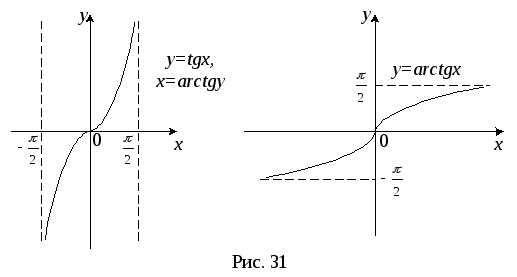6. Обратная тригонометрическая функцияy=arcctgx

Рассмотрим функцию y=ctgx на интервале (0, ). При этих значениях x функция ctgx убывает, а ее значения заполняют интервал (–, +). Поэтому она имеет обратную функцию, которая обозначается так: x=arcctgy. Эта функция определена на всей числовой оси, а ее значения заполняют интервал (0, ). График функции y=arcctgx изображен на рис. 32.