Элементарные функции

Основными элементарными функциями называются следующие функции:

1) (– константа),

2) – степенная (– вещественное число),

3) – показательная (),

4) – логарифмическая (,),

5) тригонометрические ,

6) обратные тригонометрические .

7)Гиперболические функции:

–синус гиперболический, – косинус гиперболический,– тангенс гиперболический ,– котангенс гиперболический.

Элементарными называются функции которые содержат конечное число арифметических операций над основными элементарными функциями и конечное число композиций (суперпозиций) основных элементарных функций.

Элементарные функции подразделяются на следующие классы:

1) Полиномы – функции вида

,

–старшая степень полинома.

2)Дробно-рациональные (функции, представляющие собой отношение двух полиномов):

3)Иррациональные функции – функции, которые получаются с помощью суперпозиции рациональных функций, а также степенных функций с рациональными показателями и четырёх арифметических действий.

4)Трансцендентные функции – функции, которые не являются рациональными или иррациональными. Это тригонометрические, показательные, обратные тригонометрические, логарифмические, гиперболические функции.

Банк функций

1. Линейная функция

Функцию вида , гдеk и b – действительные числа, называют линейной. Если k=0, то получим постоянную функцию y=b.

I. Область определения: множество R всех действительных чисел.

II.График линейной функции есть прямая. Для построения прямой достаточно двух точек. Графиком постоянной функции y=b является прямая, параллельная оси абсцисс и проходящая через точку (0; b) на оси ординат. На рис. 1 изображены графики нескольких постоянных функций. В частности, графиком функции y=0 является ось абсцисс.

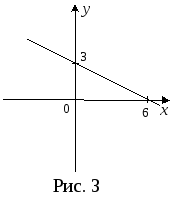
Графиком функции y=kx является прямая, проходящая через начало координат (рис. 2). Для построения графика y=kx+b достаточно найти две любые точки, принадлежащие графику. Построим, например, график функции. Составим таблицу . Отметим на координатной плоскости точки (0; 3), (2; 2) и проведем через эти точки прямую. Это и есть искомый график (рис.3).

III. Коэффициент k характеризует угол, который образует прямая с положительным направлением оси ox, поэтому k называется угловым коэффициентом. Если k>0, то этот угол острый и данная функция будет возрастающей; если k<0, то угол тупой и данная функция будет убывающей.

IV. Нули функции. Нулями функции y=kx+b являются корни линейного уравнения kx+b=0. Если , то– единственный корень. Приk=0, b0 уравнение не имеет корней. При k=0, b=0 уравнение kx+b=0 выполняется при xR. На графике нули функции –­ это абсциссы точек пересечения с осью ox. В первом случае график y=kx+b пересекает ось ox в единственной точке , во втором случае графикy=b (b0) не пересекает ось ox, в третьем – график функции y=0 совпадает с осью ox.

2. Квадратичная функция

Функция вида y=ax²+bx+c, где a, b, c – действительные числа и a0, называется квадратичной.

1. Областью определения функции является множество действительных чисел.

2. Выделение полного квадрата. Квадратичную функцию y=ax²+bx+c всегда можно привести к виду y=a(x+m)²+p, т.е. выделить полный квадрат:

.

Например,

.

3. Графиком функции y=ax²+bx+c является парабола. Ось параболы проходит через ее вершину. Координаты вершины: ;.

Пример. Построить график функции y=3x²+12x+9.

Выделив из квадратичного трехчлена полный квадрат, получимy=3(x+2)²–3. Строим сначала график функции y=3x², а затем, используя параллельный перенос, получим искомый график – параболу с вершиной в точке (–2; –3) (рис. 5). Заметим, что параболу можно построить и по характеристическим точкам, т.е. по координатам вершины и точкам пересечения с осями координат, о чем будет сказано дальше.

4. Решение полного квадратного уравнения ax²+bx+c=0, где a0, b0, c0 зависит от дискриминанта D=b²–4ac. Если D<0, уравнение не имеет действительных решений. Если D=0, то оно примет вид , откуда получаем– единственный корень. ЕслиD>0, то уравнение имеет два различных действительных корня: ,.

Соответственно график квадратичной функции y=ax²+bx+c:

– при D<0 не имеет точек пересечения с осью ox;

– при D=0 имеет единственную точку касания с осью ox;

– при D>0 имеет две точки пересечения.

5. Рассмотрим еще один способ построения графика квадратного трехчлена y=ax²+bx+c по его корням.

Пусть x₁ и x₂ – корни квадратного трехчлена ax²+bx+c (корнями квадратного трехчлена называются корни соответствующего квадратного уравнения ax²+bx+c=0). Тогда парабола, служащая графиком функции y=ax²+bx+c, пересекает ось абсцисс в точках A(x₁; 0) и B(x₂; 0), а ось параболы проходит через точку C – середину отрезка AB, абсцисса которой . Зная абсциссу вершины параболы, найдем ее ординату, а затем построим параболу по трем точкам.

Пример. Построить график функции y=3x–x².

Из уравнения 3x–x²=0 находим корни x₁=0; x₂=3. Значит, мы знаем две точки искомой параболы A(0; 0), B(3;0). Уравнение оси параболы будет . Подставив значениев уравнениеy=3x–x², найдем . Таким образом, вершиной параболы служит точка. По трем точкамA, B, C строим параболу (рис.6).

Пример. Построить график функции y=x²–4x+4.

Свернув формулу в правой части равенства, получим y=(x–2)², следовательно, график данной функции касается оси ox в точке 2 (рис. 7).

Замечание. Если квадратный трехчлен ax²+bx+c не имеет действительных корней, то график функции y=ax²+bx+c проходит: при a>0 выше оси ox, при a<0 ниже оси ox.

6. Найдем интервалы знакопостоянства функции, т.е. решим неравенства ax²+bx+c<0 и ax²+bx+c>0 (a0).

Пустьa>0. Возможны три случая (рис. 8, 9, 10)

Из рисунков видно, что если D>0 (рис. 8), то ax²+bx+c<0 при x(x₁; x₂); ax²+bx+c>0 при . В случаеD=0 (рис.9) неравенство ax²+bx+c0 выполняется при всех x, неравенство ax²+bx+c0 решений не имеет. В случае D<0 (рис. 10) неравенство ax²+bx+c>0 выполняется при всех x, неравенство ax²+bx+c0 решений не имеет.

В случае, еслиa<0, рассуждаем аналогично. Графики функций будут иметь вид, представленный на рис. 11, 12, 13

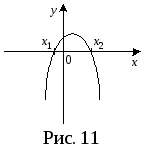
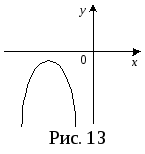
Из рисунков видно, что, если D>0 (рис. 11), ax²+bx+c>0 при x(x₁; x₂); ax²+bx+c<0 при . В случаеD=0 (рис. 12) неравенство ax²+bx+c>0 решений не имеет, ax²+bx+c0 выполняется при любых значениях x. В случае D<0 (рис. 13) неравенство ax²+bx+c0 решений не имеет, неравенство ax²+bx+c<0 выполняется при любых значениях x.

7. Монотонность функции. Квадратный трехчлен ax²+bx+c имеет единственную критическую точку . Из рис. 8-13 видно, что еслиa>0, то функция возрастает при и убывает при, еслиa<0, то функция возрастает при и убывает при.