
- •Глава VI: Предел и непрерывность функции в точке
- •6.0. Главные песни о старом. Определение функции
- •Свойства функций
- •Элементарные функции
- •1. Линейная функция
- •2. Квадратичная функция
- •3. Функция
- •4. Дробно-линейная функция
- •17. Гиперболические функции:
- •3. Преобразование графиков
- •3.1. Сдвиг
- •3.2. Изменение масштаба
- •3.4. График функции f(|X|)
- •3.5. Функция типа «единица на эф»
- •3.6. Обратная функция.
- •3.7. Построение графиков композиций функций
- •3.8. Построение асимптотических портретов функций
- •6. 2 Замечательные пределы
- •1. Первый замечательный предел .
- •2. Второй замечательный предел .
- •6. 3 Непрерывность функции в точке
- •6. 4 Бесконечно малые функции и их сравнение
- •6. 5 Свойства функций, непрерывных на промежутке
3.7. Построение графиков композиций функций
Под композицией функции будем понимать функцию от функции. Для того чтобы построить эскиз графика такой функции, надо последовательно построить каждую из составляющих функций и провести исследование изменений аргументов каждой из них.
Примеры.
1. Построить график
![]() .
Эту функцию можно представить в виде
суперпозиции функцийy=arctgU;
.
Эту функцию можно представить в виде
суперпозиции функцийy=arctgU;
![]() ;V=x–1.
;V=x–1.
х
+ V
+ U
0+ y
0+
+ V
+ U
0+ y
0+
х
1+ V
0+ U
0+ y
![]() –
–
х
1– V
0– U
– y
–![]() +
+
х – V – U 0– y 0–
Таким образом, мы выяснили поведение у при изменении х. По результатам этого исследования можно построить эскиз графика.
2 .
Построить эскиз графика функции
.
Построить эскиз графика функции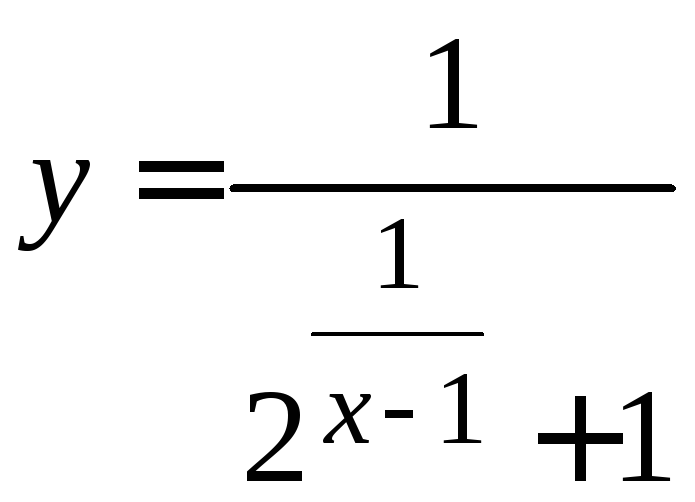 .
Эта функция есть суперпозиция следующих
функций:
.
Эта функция есть суперпозиция следующих
функций:![]() ;U=1+V;
V=2t;
;U=1+V;
V=2t;
![]() ;g=x–1.
;g=x–1.
И

 х
графики имеют вид:
х
графики имеют вид:
Исследуем их поведение, и на основании этого исследования построим график.
|
х + |
g + |
t 0+ |
V 1+ |
U 2+ |
y
|
|
х 1+ |
g 0+ |
t + |
V + |
U + |
y 0+ |
|
х 1– |
g 0– |
t – |
V 0+ |
U 1+ |
y 1– |
|
х – |
g – |
t 0– |
V 1– |
U 2+ |
y
|
 Задание.
1. Построить графики функций: а)
Задание.
1. Построить графики функций: а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
г)
;
г) .
.
3.8. Построение асимптотических портретов функций
В тех случаях, когда не работают описанные выше методы, общий характер поведения функции можно установить асимптотическим исследованием. Схема этого исследования такова.
А. Общие свойства. Надо ответить на следующие вопросы:
ОДЗ;
симметричность;
особенности – выявляем точки, в которых функция не определена, и точки, в которых она хорошо считается («хорошие» точки).
В. Асимптотические свойства.
 –
горизонтальные асимптоты;
–
горизонтальные асимптоты;
 y=kx+b
– наклонная асимптота;
y=kx+b
– наклонная асимптота;
 –
вертикальная асимптота.
–
вертикальная асимптота.
Здесь а1, а2, … ,аi, … ,аn – точки, в которых функция не определена. Именно они определяют вертикальные асимптоты. Наклонной асимптотой y=kx+b (при k=0 – горизонтальной) называется прямая, разность между которой и функцией стремится к нулю по мере того, как х стремится к бесконечности. Вертикальной асимптотой х=аi называется прямая, разница между которой и функцией стремится к нулю по мере того, как хаi+ и хаi–.
Далее рисуем «сетку», т.е. систему координат со всеми асимптотами и «хорошими» точками, и по результатам исследования рисуем асимптотический портрет. Полученный эскиз графика уточняется с использованием первой и второй производных, но этим мы здесь заниматься не будем.
Примеры.
1. Построить график функции
 .
.
А. 1. D: x(–; –2)(2; +).
2. f(–x)= –f(x) – функция нечетная.
3. Эта функция имеет конечное число точек, в которых она не определена, следовательно, она непериодична (докажите эту теорему!)
4.
![]() (в этих точках функция не определена).
Хорошие точки y(0)=0;
(в этих точках функция не определена).
Хорошие точки y(0)=0;
![]() .
.
В. 1. х + у +.
х
+ ![]() .
.
х
+ 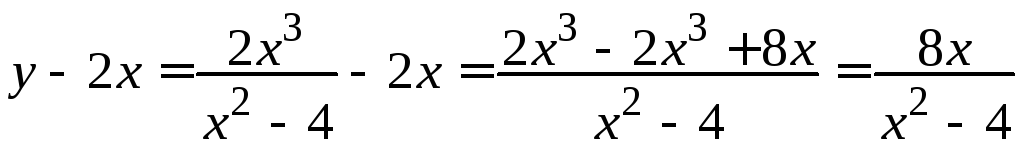 .
.

П оскольку
функция симметрична (нечетна), то
достаточно построить ее в правой
полуплоскости и продолжить нечетным
образом на левую полуплоскость. По
результатам исследования строим график:
оскольку
функция симметрична (нечетна), то
достаточно построить ее в правой
полуплоскости и продолжить нечетным
образом на левую полуплоскость. По
результатам исследования строим график:
2.
 .
. .
.
А. 1. D: хR.
2. f(–x)f(x); f(–x)–f(x), т.е. функция общего вида, непериодическая.
3.
у(0)=0;
![]() ;у(–1)=2.
;у(–1)=2.
В .х
+;
у0–;
х
–;
у0+.
Наклонных асимптот нет, так как степень
числителя меньше степени знаменателя.
Вертикальных асимптот нет, так как нет
точек, в которых функция не определена.
Строим эскиз графика. Пунктиром нарисована
та часть графика, которую можно только
угадать. Более подробное исследование
требует использования производных.
.х
+;
у0–;
х
–;
у0+.
Наклонных асимптот нет, так как степень
числителя меньше степени знаменателя.
Вертикальных асимптот нет, так как нет
точек, в которых функция не определена.
Строим эскиз графика. Пунктиром нарисована
та часть графика, которую можно только
угадать. Более подробное исследование
требует использования производных.
Задания для самостоятельной работы
Из изображенных на рис. 1–10 множеств точек выберите те, координаты x и y которых удовлетворяют заданному условию:
|
1) 4x2+y22(|x|+|y|); |
2)
|
3) ||y|–|x||=2; | |||
|
4) |x+2|+|y–1|=1; |
5) ||x|+||y|–3|–3|=1; |
6) ||y|+||x|–3|–3|=1; | |||
|
7) |y–x|+x+y=2; |
8) x+y–|y–x|=4; |
9) |x|+|y|+|x–y|2; |
10) |y|=x2–4|x|+3.
| ||




Ответы: 1) рис. 9; 2) рис. 1; 3) рис. 2; 4) рис. 5; 5) рис. 4; 6) рис. 8; 7) рис. 10; 8) рис. 6; 9) рис. 3; 10) рис. 7.
п. 6.1 Определение предела функции в точке
Определение
 1
1
![]() -окрестностью
точки
-окрестностью
точки
![]() называют интервал
называют интервал![]() и обозначают
и обозначают![]() (или
(или![]() ).
).
Определение 2
 крестность
крестность![]() называютпроколотой,
если из
называютпроколотой,
если из
![]() исключена сама точка
исключена сама точка![]() ,
и обозначается
,
и обозначается![]() (или
(или![]() ).
).
Определение 3
Говорят,
что функция
![]() имеет в точке
имеет в точке
![]() предел,
равный
предел,
равный
![]() ,
если для любой последовательности точек
,
если для любой последовательности точек![]() ,
сходящейся к точке
,
сходящейся к точке![]() ,
последовательность значений
,
последовательность значений![]() сходится к числу
сходится к числу![]() и обозначается
и обозначается![]() .
.
Замечание
1 Функция
![]() может быть не определена в самой точке
может быть не определена в самой точке![]() .
.
Замечание 2 Так как предел функции есть более сложноорганизованный предел последовательно-сти, то имеют место все теоремы о пределах последовательностей.
Пример
Вычислим
![]() .
.
Выберем
любую последовательность
![]() :
:![]() .
Тогда
.
Тогда![]()
 .
.
Пример
Вычислим
![]() .
.
Выберем
любую последовательность
![]() такую, что
такую, что![]() .
Тогда возникает неопределенность
.
Тогда возникает неопределенность![]() .
Воспользуемся тем, что для любого
.
Воспользуемся тем, что для любого![]() .
Тогда
.
Тогда![]() .
.
Пример
Рассмотрим
функцию Дирихле
![]() ,
(
,
(![]() - множество рациональных чисел).
- множество рациональных чисел).
Если
взять последовательность
![]() ,
где
,
где![]() ,
то
,
то![]() ;
если же
;
если же![]() такова, что
такова, что![]() ,
то
,
то![]() .
Значит, функция Дирихле не имеет предел
ни в одной точке действительной оси,
так значение предела зависит от выбора
последовательности
.
Значит, функция Дирихле не имеет предел
ни в одной точке действительной оси,
так значение предела зависит от выбора
последовательности![]() .
.
Теорема 1. Критерий Коши существования предела.
Для
любого
![]() ,
найдется
,
найдется![]() ,
зависящее от
,
зависящее от![]() ,
такое что
,
такое что
![]() ,следовательно
,следовательно![]() ,
что равносильно:
,
что равносильно:![]()
![]() (1)
(1)
Доказательство:
Необходимость.
Пусть
соотношение (1) выполняется. Покажем,
что для любой последовательности
![]() ,
последовательность
,
последовательность![]() стремится к
стремится к![]() при
при![]() .
Выберем какое-нибудь
.
Выберем какое-нибудь![]() .
По
.
По![]() найдем
найдем![]() из неравенства
из неравенства![]() ,
т.е. определим окрестность
,
т.е. определим окрестность![]() .
Зная
.
Зная![]() ,
можно найти номер
,
можно найти номер![]() ,
начиная с которого
,
начиная с которого![]() попадает в
попадает в![]() (
(![]() - коридор точки
- коридор точки![]() ).
Тогда в силу соотношения (1) имеем
).
Тогда в силу соотношения (1) имеем![]() .
Это означает, что выполняется соотношение
(**) для последовательности
.
Это означает, что выполняется соотношение
(**) для последовательности![]() ,
т.е.
,
т.е.![]() .
.
Достаточность.
Пусть
существует
![]() .
Покажем, что выполняется соотношение
(1). Воспользуемся методом от противного.
.
Покажем, что выполняется соотношение
(1). Воспользуемся методом от противного.
Пусть
соотношение (1) не выполняется, т.е.
![]() .
.
Так
как
![]() ,
то выполняется соотношение (**), т.е.
найдется номер
,
то выполняется соотношение (**), т.е.
найдется номер![]() ,
начиная с которого
,
начиная с которого![]() .
Так как
.
Так как![]() любое, то выберем в качестве
любое, то выберем в качестве![]() .
Тогда
.
Тогда![]() .
По теореме о «двух милиционерах» при
.
По теореме о «двух милиционерах» при![]()
![]() .
Но тогда в силу определения 2
последовательность
.
Но тогда в силу определения 2
последовательность![]() ,
т.е.
,
т.е.![]() (имеет место соотношение (**)). Получили
противоречие.
(имеет место соотношение (**)). Получили
противоречие.
Определение 4.
Определение по Коши
Говорят,
что функция
![]() имеет в
точке
имеет в
точке
![]() предел,
равный
предел,
равный
![]() ,
если
,
если![]()
![]() ,
т.е. выполняется соотношение (1).
,
т.е. выполняется соотношение (1).
Замечание
3
Сформулируем определение предела
функции
![]() в точке
в точке![]() на языке окрестностей:
на языке окрестностей:
![]()
![]() (
(![]() -
окрестность точки
-
окрестность точки![]() );
);
или
![]() .
.
Пример
Докажем,
что
![]() .
.
Так
как
![]() ,
то для любого
,
то для любого![]() выберем
выберем![]() .
При этом для всех
.
При этом для всех![]() таких, что
таких, что![]() получим
получим![]() .
Таким образом,
.
Таким образом,![]()
![]() ,
т.е.
,
т.е.![]() .
.
Пример Докажем, что не существует предела функции
![]() в
точке
в
точке
![]() .
.
Рассмотрим
последовательности
![]() и
и![]() .
При
.
При![]()
![]() ,
но
,
но![]() .
Значит,
.
Значит,![]() .
.
Определение 5
Число
![]() называетсяпределом
функции
называетсяпределом
функции
![]() в точке
в точке
![]() слева,
если
слева,
если
![]()
![]() .
При этом число
.
При этом число![]() называютлевым
пределом
функции
называютлевым
пределом
функции
![]() в точке
в точке![]() .
.
Аналогично
вводится понятие правого
предела
![]() функции
функции![]() в точке
в точке![]() .
.
Теорема
2 Для
того, чтобы существовал предел
![]() ,
необходимо и достаточно, чтобы в точке
,
необходимо и достаточно, чтобы в точке![]() существовали односторонние пределы
существовали односторонние пределы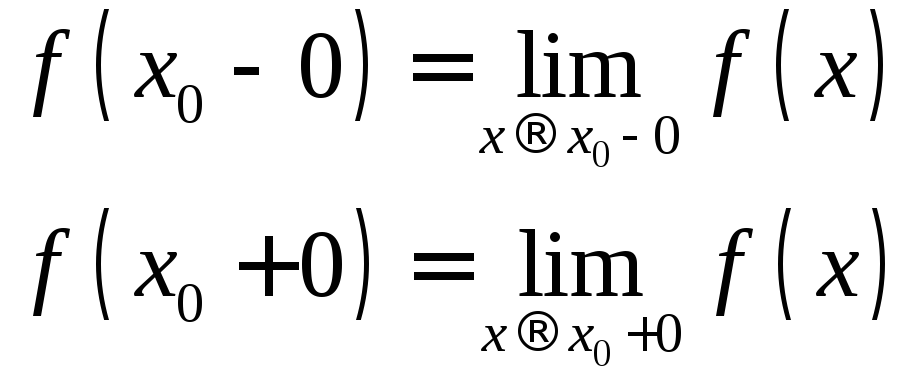 ,
причем
,
причем![]() .
.
Доказательство:
Необходимость.
Пусть
существует
![]() ,
т.е.
,
т.е.![]() .
Выберем последовательность
.
Выберем последовательность![]() такой, что
такой, что![]() .
Тогда получаем существование
.
Тогда получаем существование![]() ,
причем
,
причем![]() .
.
Для
доказательства существования
![]() достаточно выбрать любую последовательность
достаточно выбрать любую последовательность![]() ,
такую, что
,
такую, что![]() .
.
Достаточность.
Пусть
существует
![]() ,
т.е.
,
т.е.![]() ,
,![]() .
.
Выберем
![]() .
Тогда для любого
.
Тогда для любого![]()
![]() .
.

