17. Гиперболические функции:

–синус гиперболический, – косинус гиперболический,– тангенс гиперболический ,– котангенс гиперболический.

, .

Гиперболические функции можно выразить через тригонометрические и наоборот.

3. Преобразование графиков

3.1. Сдвиг

График функции у=f(x–a)+b совпадает с графиком функции y=f(x), если Х=х–а, Y=у–b – новые оси координат.

3.2. Изменение масштаба

График функции y=af(x) совпадает с графиком функции y=f(x), если сделано масштабное преобразование осей координат по правилу Х=x, . В частном случаеа= –1 происходит зеркальное отражение от оси х, а в частном случае = –1 – от оси у.

Пример. y=kx+b.  Y=y–b; X=kX. Когда Y, т.е. y=b, проводим новую ось х. Масштаб вдоль этой оси снимается в k раз в новых осях с новым масштабом строим прямую Y=X. Этот же график можно построить непосредственно через 2 точки, как и в п. 2.1.

Пример. y=cosx. Так как , то график этой функции совпадает с графиком функцииY=sinX, если Y=y, .

3.3. График функции y=|f(x)|

По определению модуля,

Таким образом, график функции y=|f(x)| совпадает с графиком функции f(x) в верхней полуплоскости и зеркально отражается от оси в нижней полуплоскости.

3.4. График функции f(|X|)

Этот график получается зеркальным отражением правой полуплоскости графика y=f(x) на левую.

3.5. Функция типа «единица на эф»

Пусть дана функция y=f(x). Она может касаться или пересекать ось абсцисс, а может проходить выше нее. Соответственно рассмотрим обе возможности.

а) Рассмотрим только точких₀ и х₁ (а):

х + f(x)+

хх₀ + f(x)min

хх₀ – f(x)min

хх₁ + f(x)max

хх₁ – f(x)max

х – f(x)+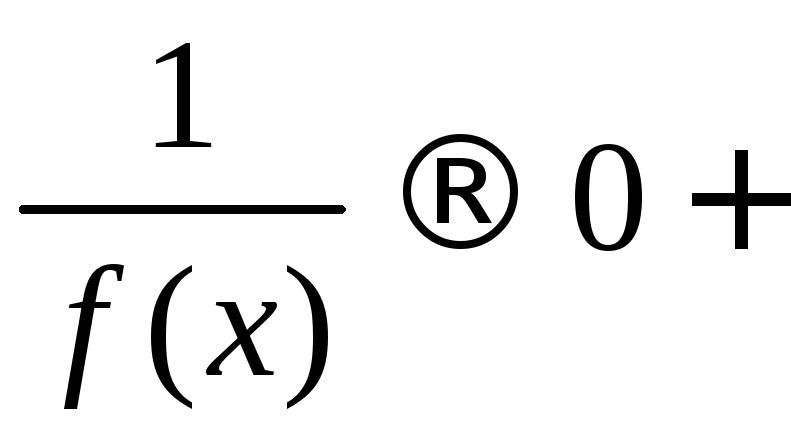

(запись ха+ читается: х стремится к а со стороны плюсов, т.е. справа, а уа+ означает: у стремится к a со стороны плюсов, т.е. сверху).

На основании этого исследования строим график . Рассмотрим только точких₀ и х₁ (б):

х + f(x) –

хх₀ + f(x) 0 –

хх₀ – f(x) 0 +

хх₁ + f(x)max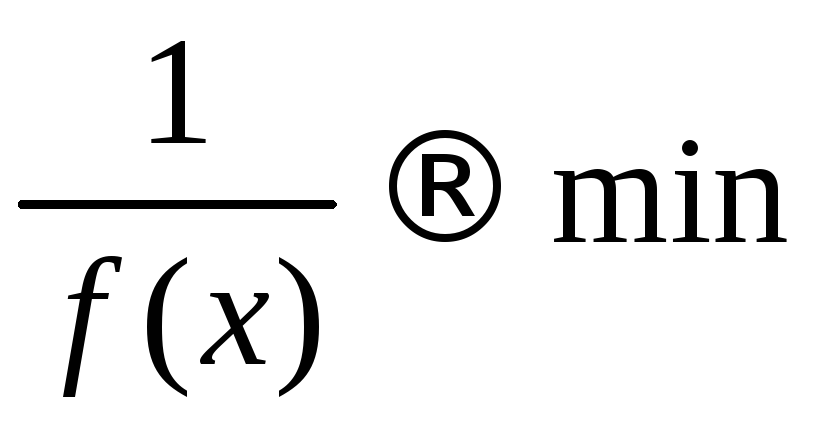

хх₁ – f(x)max

х – f(x)+

На основании этого исследования строим график.

3.6. Обратная функция.

Пусть функция y=f(x) задана на сегменте [a, b], а множеством ее значений на этом сегменте является сегмент [, ]. Если каждому y[, ] соответствует единственное значение x[a, b], для которого y=f(x), то на [, ] можно определить функцию x=(y). Эта функция называется обратной по отношению к функции y=f(x), т.е. f((y))=y, f((x))=x. Очевидно, что y=f(x) и x=f(y) описывают одну и ту же функцию на плоскости XOY. Но принято значения аргументов откладывать по оси x, а значения функции – по оси y, т.е. вместе с функцией y=f(x) рассматривать ее обратную функцию как y=(x). Тогда очевидно, что графики прямой и обратной функций будут симметричны относительно биссектрисы 1-го и 3-го координатных углов.

Примеры. 1.  у=5х+7. Эта функция монотонно возрастает на всей числовой оси, и каждому у соответствует единственное значение , тогда функциябудет обратной функцией по отношению к функцииу=5х+7. Достаточным условием существования обратной функции (но не необходимым!) является строгая монотонность «прямой» функции y=f(x). При этом, если функция y=f(x) возрастает (убывает), то и обратная функция возрастает (убывает). График обратной функции совпадает с графиком прямой, если аргументом считать теперь у, но, как уже отмечалось, аргументом будем считать х, тогда график обратной функции получается из графика прямой зеркальным отражением от биссектрисы 1-го и 3-го координатных углов. Обозначается обратная функция так: y=f ^–1(x). Таким образом, она может пересекаться с прямой функцией только на прямой у=х.

2. y=sinx. Очевидно, что для этой функции не выполнено условие существования обратной функции. Разобьем ось х на промежутки ; еслиk=2 (четное), то на них функция y=sinx возрастает, если k=n+1 (нечетное), то на этих промежутках y=sinx убывает. Причем на концах промежутков |y|=1. Таким образом, на каждом из этих промежутков существует обратная функция, определенная на [–1; 1] и называемая y=arcsinx. Отрезок называется основным (k=0), и на нем определена обратная функция y=arcsinx, симметричная на этом промежутке относительно биссектрис 1-го и 3-го координатных углов функции y=sinx. Аналогично определяются остальные обратные тригонометрические функции. Мы их изобразим на одном чертеже.

Пример. Построить обратную функцию на промежутках монотонности:

а)–f(x)=a^x; б) –f(x)=х².

Ответ:

2. Может ли немонотонная функцияy=f(x), х(–; +) иметь обратную? Рассмотрите пример:

Указание. Может, если уравнение y=f(x) при каждом фиксированном у(–; +) имеет единственное решение. Обладает ли этим свойством предложенная функция?