Глава VI: Предел и непрерывность функции в точке

6.0. Главные песни о старом. Определение функции

Если сравнить математику с картиной, прекрасной или безобразной– это дело вкуса, то гвоздь, на котором эта картина держится, и есть понятие функции.

Пусть имеется два множества произвольной природы: x и y, причем xX– элемент множества X, а yY– элемент множества Y.

1. Если каждому элементуxX соответствует единственный элемент yY, то правило такого соответствия и его результат называются функцией. Ее обозначения: y=f(x); f:xy; . МножествоX называется областью определения или областью допустимых значений (ОДЗ) функции y=f(x), а элемент xX называется независимой переменной или аргументом, множество Y– областью изменения, или множеством значений функции, а элемент yY тоже называется функцией (результат соответствия). Обычно под ОДЗ понимается система неравенств, описывающих область определения, а решение этой системы, т.е. сама область определения, обычно обозначается буквой D; множество значений функции обозначается буквой E. В дальнейшем мы будем рассматривать функции, заданные на числовых множествах. Понятие функции, как правила соответствия между элементами двух множеств, часто используется в задачах.

Примеры.

1)  f(x)=3x–2, g(x)=5x+7. Решить уравнение f(g(x))–g(f(x))=f(f(x))–g(g(x)).

3(5x+7)–2–(5(3x–2)+7)=3(3x–2)–2–(5(5x+7)+7), .

2) Если f(x²–3x)=2x²–6x+5 и f(x)–линейная функция, то f(3)=?

Так как f(x)–линейная функция, то f(x)=kx+b, т.е. 2x²–6x+5=k(x²–3x)+b, т.е.

2(x²–3x)+5=k(x²–3x)+b, т.е. k=2, b=5, f(x)=2x+5, f(3)=11.

2. Графиком функции y=f(x) называется геометрическое место всех упорядоченных пар (x, y), таких, что первый элемент пары принадлежит области определения функции, а второй – области ее изменения. [Напомним, что под геометрическим местом точек (ГМТ) понимается любое множество точек, обладающих определенными, общими для них свойствами, причем никакие другие точки плоскости (пространства) этими свойствами не обладают.]

П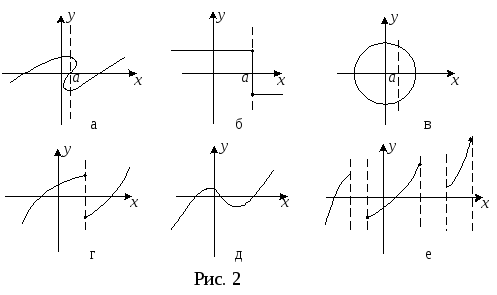римеры

На рис. 2, а, б, в, г изображены линии, не являющиеся функциями, так как при x=a соответствующие значения y=f(x) не единственны. На рис. 2, д, е даны примеры функции.

Задание: дополнить график на рис. 2, е так, чтобы он: изображал функцию; изображал не функцию.

Замечание. Термин «функция» (functus(лат.) – выполнять) с 1673 года стал употреблять знаменитый философ и математик Готфриб Вильгельм Лейбниц, правда, в смысле дополнительных вычислений и построений, облегчающих решение задачи. Современное определение функции дали Н.И. Лобачесвкий и Лежен Дирихле в середине XIX века. В частности, под это определение попадает функция, получившая название функции Дирихле D(x)=0, если x– рациональное число; D(x)=1, если x– иррациональное число.

Если функцию рассматривать как отображение, то элементназываютобразом элемента . Элемент жев этом случае называютпрообразом элемента .