УМ_Пособие_09

61

pk = – f'(xk)·(f '(x0))–1.

Шаг 4. Определяется следующая точка xk+1 = xk + ·pk, где – решение задачи одномерной минимизации функции

φ( ) = f(xk + ·pk), при ≥ 0.

Шаг 5. В точке xk+1 вычисляется градиент f'(xk+1)

Шаг 6. Если ||f'(xk+1)|| ε3, то поиск заканчивается и

Иначе k = k + 1 и переход к шагу 3.

В рассмотренной схеме для выбора шага k используется способ аналогичный приему, используемому в методе наискорейшего спуска. Но можно было бы воспользоваться и способом аналогичным используемому в градиентном методе с пропорциональным шагом.

Другая модификация метода Ньютона связана с обновлением матрицы вторых производных через определѐнное количество шагов. Формула вычисления очередной точки xk+1, в этом случае, будет выглядеть следующим образом:

хjm+i+1 = xjm+i – jm+i· (f''(xjm)) –1·f'(xjm+i),

jm+i ≥ 0, k = jm + i, j = 0, 1, 2, …, i = 0, 1, …, m –1.

Здесь m > 0 – целое число, определяющее количество шагов через которое происходит обновление матрицы вторых производных f''(x). Этот метод занимает промежуточное положение между методом Ньютона и его модификацией I.

Градиентные методы в задачах с ограничениями

Если оптимум целевой функции находится внутри допустимой области G(X) изменения переменных X, то присутствие ограничений не влияет на процесс поиска решения. Поиск оптимума осуществляется практически так же, как и в случае без ограничений. Если же оптимум функции находится за пределами допустимой области, то отыскание наибольшего значения целевой функции при ограничениях на X становится существенно сложнее.

Одним из эффективных методов решения задач с ограничениями является метод штрафных функций. Идея метода состоит в следующем. Вместо того, чтобы

62

непосредственно решать задачу с ограничениями, переходят к задаче оптимизации вспомогательной функции R(X)=f(X)+H(X), в которой на X не накладывается каких-либо ограничений.

Добавление слагаемого Н(Х) (отрицательного в задачах на максимум) к функции f(X) можно рассматривать как введение специального штрафа за неточное выполнение ограничений gj(X)=0, j=I,2,...,m. Поэтому слагаемое Н(Х) часто называется штрафной функцией. Таким образом, метод штрафных функций позволяет сводить задачи на условный экстремум к задачам на безусловный экстремум.

Основное требование к функциям штрафа сводится к тому, что они должны быть равны нулю для тех X, при которых ограничения выполняются, и должны быть отрицательны (в задачах максимизации) для тех X, при которых ограничения нарушаются.

В зависимости от вида ограничений используются различные виды функций штрафа.

Если ограничения представляют собой равенства и нестрогие неравенства используют штрафные функции:

В случае, если эксперимент вышел за пределы ДОР, штрафная функция резко возрастает (или убывает) при поиске минимума (максимума) и возвращает исследование в ОДР. Метод с функциями штрафа такого типа называют методом внешней точки.

Если ограничения представляют собой строгие неравенства, то используются барьерные функции, значение которых неограниченно возрастает (убывает) при поиске максимума (минимума) при приближении к границе ОДЗ. Барьерная функция должна быть непрерывной внутри ДОР. Т.к. все исследуемые при этом точки лежат внутри ОДР, данный метод называют методом внутренней точки. В качестве барьерной часто применяется логарифмическая функция вида:

64

при ограничениях

-2х1 - 3х2 + 6 ≥ 0; х1 - 4х2 + 5 ≥ 0;

х1,х2≥0 Найдем выражения для частных производных целевой

функции и каждой функции ограничений. Получим

Выберем значения Х0=(0,0); h=0.2; α=2. Тогда алгоритм

движения по каждой из координат примет вид x1k+1=max{0, xlk + 0.2[1 - 2 xlk + α1(Xk)(-2) + α2(Xk)(-1)]}; x2k+1=max{0, x2k + 0.2[2 - x2k + α1(Xk)(-3) + α2(Xk)(-4)]}

Чтобы перейти к расчету координат точки X1, найдем сначала значения α1(X0) и α2(X0), зависящие от того, выполняются ли в точке X0 ограничения задачи. Поскольку в точке (0;0) оба ограничения выполняются, то α1 = 0, α2 = 0. Итак,

в начальной точке поиска имеем X0 = (0, 0), f(X0) = 0, α1(X0) = 0,

α2(X0) = 0.

Первый шаг. Выполняем расчет координат точки X(1):

х1(1) = max{0; 0 + 0.2[l – 0 + 0 + 0]} = 0.2; х2(1) = max{0; 0 + 0.2[2 - 0 + 0 + 0]} = 0.4.

Проверяя ограничения, видим, что в точке Х1 = (0,2;0,4) они оба выполняются. Следовательно, α1(X1) = 0; α2(X1) = 0. Вычисляем f(X1)=0.88.

Второй шаг.

х1(2) = max{0; 0.2 + 0.2[1 - 0.4 + 0 + 0]} = 0,32; х2(2) =max {0; 0.4 + 0.2[2 - 0.4 + 0 + 0]} = 0,72; α 1(X2) = 0; α 2(Х2) = 0; f(X2) = 1.4.

Третий шаг.

х1(3) =max{0; 0,32 + 0,2[1 - 0,64 + 0 + 0]} = 0,4; х2(3) =max{0; 0,72 + 0,2[2 - 0,72 + 0 + 0]} = 1;

Четвертый шаг.

65

х1(4) = max{0; 0,4 + 0,2[1 - 0,8 + 0 + 0]} = 0,44; х2(4) = max{0;1 - 0,2[2 - 1 + 0 + 0]} = 1,2.

Проверяем выполнение ограничений. Первое ограничение выполняется, а второе - нет. Следовательно, αj(X4)=0; α2(Х4)=2. Целевую функцию не вычисляем, так как точка X4 недопустима.

Пятый шаг.

х1(5) = max{0; 0,44 + 0,2[l - 0,88 + 0 - 0,2]} = 0,06; х2(5) = max{0; 1.2 + 0,2[2 -1,2 + 0 - 8]} = 0

α1(Х5) = 0; α2(Х5) = 0; f(Х5) = 0,064

При переходе границы допустимой области движущаяся точка исследования отброшена назад в допустимую область, причем довольно далеко от границы. При меньших значениях h или α "отскок" от границы был бы также меньшим. Далее поиск продолжается согласно вышеописанному алгоритму.

Упражнения

1.Для функции f(x1,x2) = -(x1 - 3)2 - 4(x2-2)2 найти максимальное значение методами: релаксации, градиента, наискорейшего подъема и сравнить скорость сходимости.

2.Найти максимальное значение функции

f(X) = 6x1 - 4x2 + 2x3 - 3x12 - 2x22 - 1/2х2

методом наискорейшего подъема, приняв х0=(0;0;3).

3. Определить экстремумы функций, используя один из

градиентных методов:

а) f(X) = 4x - x2 – 3 + 2x3;

б) f(X) = 2x12 - 1.5x1x2 + x22 - 5x1; в) f(X) = -2x12 + 2x1x2 - x22 + 6x2; г) f(X) = 4x12 + x22 - 1.5x1x2 + x2.

4.Максимизировать функцию f(X)= 6х1 - 2х12 + 2х1х2 - 2х22. Задачу решить методом наискорейшего подъема, выбрав в качестве исходного условие x10 = х20 = 0.

5.Выполнить 5 итераций при поиске максимального значения функции f(X) = 36x1 + 36x2 - 5x12 методом наискорейшего подъема.

6.Найти экстремум критерия оптимальности R, соответствующий точке минимума:

66

а) R = x12-x1x2 + x22 + x1 - x2; б) R = x12 - x1x2 + x22 + x1 - x2.

7. Найти минимум функции f(x1,x2) = (0.5)2x12 + x22 методом релаксации, приняв в качестве отправной точки Х0=(1,3)

8. Выполнить три итерации при поиске методом наискорейшего подъема максимума функции, заданной в примере 2. Поиск начать в следующих точках:

8.1.Х0 = (0;1;3);

8.2.Х0 = (1/3;0;-5/3);

9.Решить задачу минимизации функции f(X) = x12 + 4х22

-1 градиентными методами, приняв в качестве начальной точку Х0 = (1, 1).

10. В следующих задачах найти экстремум функции с помощью пропорционального градиентного метода и метода наискорейшего спуска (подъема), начиная итерационный

11. Составить программу, реализующую поиск минимума одним из методов Ньютона. В следующих задачах найти приближенное значение минимума с заданной точностью ε; определить количество точек, в которых пришлось производить вычисления до достижения функцией заданной точности; построить график траектории приближенных решений задачи.

11.1.f(x) = x1 – 1.2x2 + exp(0.04x1)2 + 2x22),

ε= 2·10–4, Х0 = (0, 1)

11.2.f(x) = 3x1 – 0.9x2 + exp(2.5x1)2 + 2.3x22),

ε= 4·10–4, Х0 = (1, 0)

11.3.f(x) = 17x1 – 0.3x2 + exp(2.8x1)2 + 2.7x22)

ε= 5·10–4, Х0 = (0, -1)

67

СЛУЧАЙНЫЕ /СТАТИСТИЧЕСКИЕ/ МЕТОДЫ ПОИСКА

Для решения оптимизационных задач с большим числом переменных эффективными являются методы случайного поиска. Эти методы имеют по сравнению, например, с градиентными методами несколько худшую сходимость при решении задач с небольшим числом переменных, но зато с их помощью можно решать задачи большой размерности, в том числе такие, в которых детерминированные методы "не работают".

Важным преимуществом случайных методов является их простота, а также то, что они не налагают никаких ограничений на оптимизируемую функцию.

Основным отличием случайных методов от детерминированных является введение элемента случайности в процесс поиска экстремума. В ряде случаев замена случайных параметров системы их средними значениями (математическим ожиданием) может привести к существенным ошибкам при определении оптимального решения. Методы случайного поиска экстремума применимы также для решения детерминированных задач, а обратное не возможно.

Алгоритмы случайного поиска различаются условиями выбора рабочего шага по направлению и возможностью изменения его размера в процессе поиска, а также возможностями алгоритма изменять вероятностные свойства случайности.

Для характеристики алгоритмов случайного поиска используют такие понятия, как накопление, адаптация, самообучение.

Под накоплением понимают сбор с помощью пробных шагов информации о поведении функции вблизи рассматриваемой точки для дальнейшей какой-либо оптимальной обработки этой информации и выборе эффективного направления рабочего шага.

Адаптацией называется целенаправленный процесс изменения различных параметров поиска (например, шага) для

68

повышения его эффективности. Процесс адаптации можно вводить и в детерминированные методы.

Под самообучением понимается целенаправленный процесс изменения вероятностных свойств случайности, целью которых является повышение быстродействия, точности, надежности и других характеристик поиска. Процесс самообучения доступен только случайным /статистическим/ методам.

Процесс самообучения и адаптации имеют много общего, и точную границу между ними провести трудно.

Ненаправленный случайный поиск

Наиболее полно элементы случайности используются в методе ненаправленного случайного поиска. Для описания этого метода сформулируем задачу поиска оптимальных решений как задачу поиска минимума функции W(X) векторного аргумента Х=(х1,x2,…,xn) в некоторой заданной области D допустимых значений X. Область D определяет пространство допустимых решений, каждой точке которого соответствует некоторое значение вектора X и целевой функции W(X), удовлетворяющие заданным ограничениям. Вектор X* D, соответствующий минимуму оптимизируемой функции W(X), является целью поиска.

Ненаправленный случайный (слепой) поиск экстремума производят следующим образом. Строят последовательность

X (1) (x1(1) , x2(1) ,...,xn(1) ) ; X (2) (x1(2) , x2(2) ,...,xn(2) ) ;…; X ( N ) (x1( N ) , x2(N ) ,...,xn( N ) )

независимых случайных векторов, концами которых являются точки, принадлежащие области D. Затем вычисляют соответствующие значение целевые функции

W (1) (x1(1) , x2(1) ,...,xn(1) ) ;W (2) (x1(2) , x2(2) ,...,xn(2) ) ;…; W ( N ) (x1( N ) , x2( N ) ,...,xn( N ) )

из которых выбирают наименьшую:

W (X *) min W (1) ,W (2) ,...,W (N )

69

Если задано Wmin, то поиск осуществляется до тех пор,

В основе метода лежит проведение испытаний модели с использованием выборки объема N независимых случайных чисел {хi} для выявления области вероятного экстремума.

Т.е. ненаправленный случайный поиск экстремума — это реализация метода «проб и ошибок». Его использование требует значительного количества проб (шагов). Поэтому реализация этого метода возможна в основном на базе использования ЭВМ. Сходимость метода ненаправленного случайного поиска зависит от числа n оптимизируемых параметров и от требуемой точности достижения экстремума.

Достоинство этого метода поиска экстремума состоит в том, что просматриваемое ограниченное подмножество вариантов выбирается случайным образом. Это позволяет равномерно просмотреть все множество вариантов. Кроме того, с увеличением объема выборки увеличивается вероятность попадания в точку оптимального решения задачи.

Оценка требуемого объема вычислений может проводиться в ходе поиска.

Необходимость продолжения вычислений определяется тем, насколько подробно была просмотрена область определения целевой функции.

Можно использовать следующий подход к оценке целесообразности продолжения поиска. По результатам большого числа Nl испытаний (Nl>100) строят вариационный ряд (последовательность расположенных в возрастающем порядке значений целевой функции): W1 W2 W3 ... WN и

эмпирическую интегральную функцию распределения FN1 ( ) . Если после проведения дополнительного числа

вычислений.

При реализации метода ненаправленного случайного поиска трудно получить равномерное распределение случайных точек в области D со сложной конфигурацией. Поэтому

70

приходится вписывать область D в область с простой конфигурацией, для которой получить равномерное распределение точек нетрудно. Это требует проверки принадлежности точек заданной области D на каждом шаге поиска.

Остановимся теперь на оценке эффективности метода ненаправленного случайного поиска. Пусть заданы вероятность р и точность нахождения экстремума функции W(X) в области D. Заданием точности определяется множество оптимальных решений {X*}. Отношение объема области оптимальных решений к объему области D обозначим через . Если случайные точки равномерно распределены в области D, то вероятность попадания в множество {X*} на любом шаге равна, а вероятность попадания за N шагов составляет p 1 (1 )N .

При этом необходимое число шагов для однократного попадания в область {X*} с вероятностью p определится по формуле

Nlg(1 p) . lg(1 )

Для случая, когда области D и {X*} представляют собой n-мерные гиперсферы соответственно с радиусами R и r , вероятность попадания на одном шаге (при одном испытании) составит (r 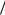R)n .

Число шагов N, необходимое для попадания в область {X*} с заданной вероятностью р, в этом случае находится по формуле

и с увеличением n растет чрезвычайно быстро. Поэтому для случая, когда, n велико, применение метода ненаправленного случайного поиска нецелесообразно.

Большая трудоемкость поиска — основной и весьма существенный недостаток метода ненаправленного поиска.