УМ_Пособие_09

21

Множители Лагранжа

Неопределѐнный множитель Лагранжа λj указывает на степень изменения величины экстремума функции при изменении параметра bj ограничения.

Действительно, если величина bj в задаче может меняться, то точка экстремума X* и, следовательно, значение max(min) f(X*) станут зависимыми от bj. Предположив, что f(х) и ограничения – линейные функции, вычислим их производные:

а т.к. f * g ,

x x

22

Множители Лагранжа можно применять для решения задач оптимизации объектов на основе уравнений с частными производными и задач динамической оптимизации. При этом вместо решения системы конечных уравнений для отыскания оптимума необходимо интегрировать систему дифференциальных уравнений.

Следует отметить, что множители Лагранжа используют также в качестве вспомогательного средства и при решении специальными методами задач других классов с ограничениями типа равенств, например, в вариационном исчислении и динамическом программировании. Особенно эффективно применение множителей Лагранжа в методе динамического программирования, где с их помощью иногда удается снизить размерность решаемой задачи.

Упражнения 1

1.Найти экстремум функций и исследовать его на максимум и минимум:

a.f (x, y) 3x3 x2 y3 3y2 1;

b.f (x, y) 4x12 4x2 3;

c.f (x) 5x12 10x1 x2 x22 6x1 3x2 ;

d.f (x) 2x12 2x1 x2 x22 9x1 6x2 .

2.Найти стороны прямоугольника максимальной площади, вписанного в круг

х2+y2=г2.

3. Найти размеры прямоугольного параллелепипеда наибольшего объема с гранями параллельными координатным плоскостям, вписанного в эллипсоид

4. Найти максимум функции f(х)= x1 x2 при условии g(x)= 3 x1 x2 2x1 x2 0 .

23

7.Найти максимальное и минимальное значения функции f = x - у при условии

24

ОДНОМЕРНЫЙ ПОИСК

Аналитические методы оптимизации позволяют решать широкий класс задач, однако они обладают и рядом существенных недостатков-ограничений, основными из них являются следующие:

1. Как целевая функция решаемой задачи, так и все функции ограничения должны принадлежать классу C1 т.е. быть непрерывными функциями, частные производные которых также являются непрерывными функциями.

требует решения нелинейной системы уравнений.

3.Целевая функция и все ограничения должны быть заданы в аналитическом виде.

Это достаточно серьезные ограничения, поэтому усилия

математиков были направлены на разработку таких методов решения экстремальных задач, для реализации которых достаточно иметь возможность определять значение целевой и ограничивающей функций в произвольной точке из области их задания любым способом. Более того, вполне этих методов допускало бы не только вычислять, но и измерять значения целевой функции, если она отражает какой-либо физический процесс. Понятно, однако, что любой из подобных методов имеет ограниченную область применения, поскольку существенно использует специфику оптимизируемой функции и допустимой области.

Наиболее разработанными методами нелинейного программирования являются методы одномерного поиска.

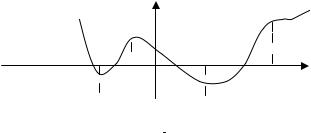
В методах одномерной оптимизации рассматривается отрезок X=[a,b], содержащей искомое решение x*. Такой отрезок называется отрезком неопределенности, или отрезком локализации. Относительно целевой функции f(x) часто предполагается, что она унимодальная.

Функция f(x) называется унимодальной на X=[a,b], если существует такая точка x* X, что

где x1<x2<x*, x1,x2 X.

25

Если ограничиваться рассмотрением лишь непрерывных функций f(x), то свойство унимодальности функции попросту означает наличие у нее единственного локального максимума (минимума) и этот максимум (минимум) достигается в точке x*.

В ряде методов относительно целевой функции f(x) предполагается, что она выпуклая на X.

Функция f(x) называется выпуклой на Х=[a,b], если для любых x1,x2, X и всех , 0 1 справедливо соотношение: f (

x1+(1- ) x2) f (x1)+(1- ) f (x2).

Если при любых x1,x2, X неравенство будет строгим, то функция f(x) называется строго выпуклой.

Непрерывная строго выпуклая функция является унимодальной. Однако не всякая унимодальная функция является выпуклой или непрерывной.

Функция f(x) имеет локальный минимум в точке Х0 (рис.1), если существует некоторая положительная величина , такая, что если |xi-x0|< , то f(xi) f(x0). Иными словами, если существует окрестность точки x0 , такая, что для всех значений хi из этой окрестности f(xi) больше f(x0), то функция f(x) имеет

хm

х0

Рис. 1

минимум в точке x0. Если для всех точек хi справедливо неравенство f(xi) f(x0), то функция f(x) имеет глобальный минимум в этой точке.

Критерий эффективности поиска

Пусть необходимо найти максимум унимодальной функции одной переменной f(х), заданной на единичном отрезке и не имеющей на ней горизонтальных участков. Функция f(x)

26

может не быть гладкой функцией, она может иметь изгибы и даже разрывы первого рода. Будем считать, что имеется возможность без всяких ошибок определять значения f(x) в любой точке 0 x 1, а определение величины f(x0) назовем «измерением» в точке x0. Для поиска максимума f(x) будем использовать результаты измерений в заданном количестве точек х.

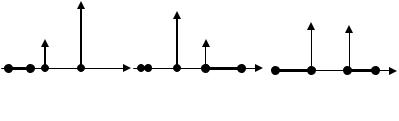
Посмотрим, какую информацию о положении максимума могут нести результаты измерений. Ясно, что результат одного измерения не позволяет сделать никакого суждения о положении максимума. Совсем иное дело, когда имеем результаты двух измерений f(x1), f(x2), причем x1< x2.

Тогда могут встретиться три случая (рис.2):

Рис. 2

1. f(x1) < f(x2) - из свойства унимодальности функции следует, что максимум не может находиться в промежутке [0, x1], поэтому этот промежуток может быть исключен из дальнейшего рассмотрения.

2. f(x1) > f(x2) - можно отбросить промежуток [x2, 1]. 3.f(x1) = f(x2) - максимум должен находиться в

промежутке [x1, x2], т.к. наша унимодальная функция не имеет горизонтальных участков.

Таким образом, в результате двух, а значит и большего числа измерений можно сократить область, в которой находится максимум, или, как мы будем говорить далее, интервал неопределенности положения максимума.

Пусть в результате n измерений длина интервала неопределенности стала ln, ясно, что сам этот интервал содержит в себе ту точку xk, в которой f(x) принимает наибольшее

28

параметров, которые обеспечили бы оптимальную близость к экстремуму.

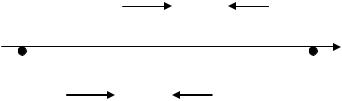
Мы уже выяснили, что минимальное число экспериментов, которое приводит к сокращению неопределенности, это два, причем 0 х1 х2 1.

Рассмотрим, в каких точках нужно проводить измерения, чтобы максимально сократить интервал неопределенности в худшем случае. Т.е. определим при каких х1 и х2 максимальный из возможных интервалов длиной 1-х1, х2, х2-х1 окажется минимальным. Очевидно, это условие можно записать так:

L*2 min L2 (x1 , x2 ) min max 1 x1 , x2 .

Нетрудно видеть, что оптимальное, на первый взгляд, решение L2=0.5, при х2=х1=0.5 отвергается из-за того, что х2>х1. Поэтому вводится минимальная величина , которая определяет погрешность измерительной аппаратуры, позволяющая при х2- х1= обнаружить разницу между соответствующими значениями y1=f(x1) и y2=f(x2). Тогда в результате экспериментов (рис.3), когда х1=0.5 - /2 и х2=0.5 + /2 можно получить не только требуемое разделение у1 и у2, но и интервал

L*2 min L2 (x1 , x2 ) min max [(0.5 + /2), (1 – (0.5 - /2)_]= 0.5 +/2

Рассмотрим случай трех разных измерений, размещение которых на единичном интервале определяется следующими

29

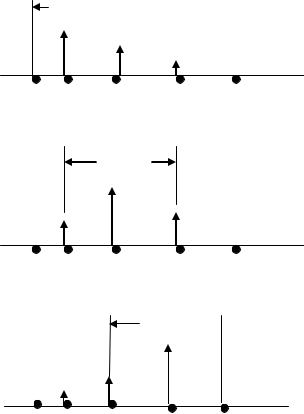
Пусть имеется некоторое размещение измерений: х1= 0.2, х2 = 0.6, х3 = 0.9. В этом случае длины возможных интервалов неопределенности изображены на рис.4.

Тогда L3 (0.2, 0,6, 0.9) = max (х2, х3-х1, 1-х2) = max (0.6, 0.7, 0.4) = 0.7.

L3=х2

L3=0.6

L

L3=0.7

L3=1-х2

L3=0.4

Рис. 4

30

Можно уменьшить L3, сблизив х1 и х3. Так, при х1=0.3, х2=0.6, х3=0.8, получим х3-х1=0.5. При этом L3 = max{0.6, 0.5, 0.4}=0.6. Теперь, перемещая х2 влево, можно еще уменьшить L3, однако будет увеличиваться величина 1-х2. Поэтому, для выбора х2 следует рассмотреть график функции max g(х2, 1-х2) в интервале 0.3 х1 х2 х3 = 0.8.

Не трудно видеть, что min max (х2, 1-х2)=0.5, при х2 =0.5.

Таким образом, оптимальной стратегией будет всякая пассивная стратегия, (х1, х2, х3), для которой х2=0.5 и х3-х1≤0.5, которая дает L*3 =0.5.

Из сравнения примеров проведения экспериментов в 2-х и 3-х точках следует, что добавление третьего эксперимента, требующего дополнительных средств и усилий в случае

пассивного поиска, мало себя оправдывает, так как разность L -

2

L = /2. Поэтому использование нечетного числа экспериментов

3

целесообразно лишь при большой погрешности измерений .

Поиск однородными парами

Из рассмотренного ранее можно сделать вывод, что существенное сокращение интервала неопределенности может дать лишь пара измерений. И если пара измерений сократила его почти в два раза, то k пар измерений может сократить этот интервал в (k+1) – раз (без учета ). Для этого достаточно все пары расположить равномерно на единичном интервале, причем расстояние между экспериментами одной пары должно составлять .

С учетом величина L*2k окажется несколько больше,

чем [1\ (к+1)]. Найдем величину L*2k . Точка предпоследнего эксперимента х2k-1 должна быть расположена на расстоянии х2k-1

последнего возможного интервала, содержащего точку х2k , есть величина интервала L2k-1 = 1 - х2k-1. Потребуем, чтобы L2k-1= L*2k , т.е.