14. Приближённое вычисление определённых интегралов

Формула Ньютона–Лейбница является хорошим средством для вычисления определённого интеграла. Однако возможности применения этой формулы сильно ограничены тем, что далеко не для всякой элементарной функции первообразная к ней является элементарной функцией. Другими словами, если f(x) является элементарной функцией, то могут оказаться неэлементарными функциями (более того, если f(x) образовать наобум как суперпозицию элементарных функций, то, скорее всего,будут неэлементарными функциями). В таком случае говорят, чтоявляется неберущимся интегралом. Приведём несколько таких примеров: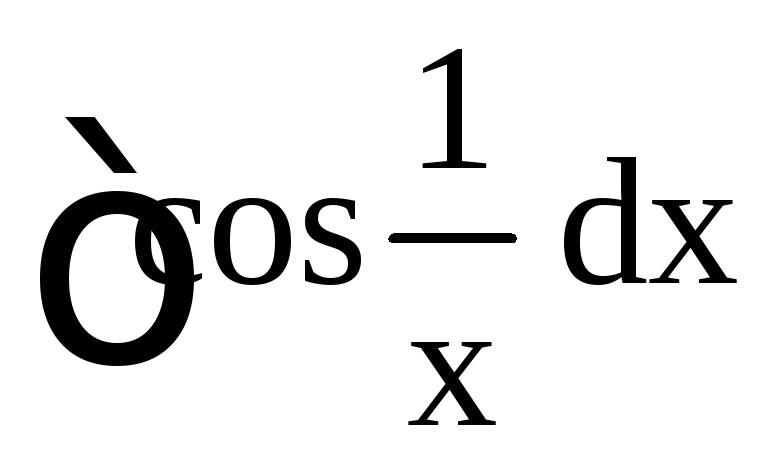,,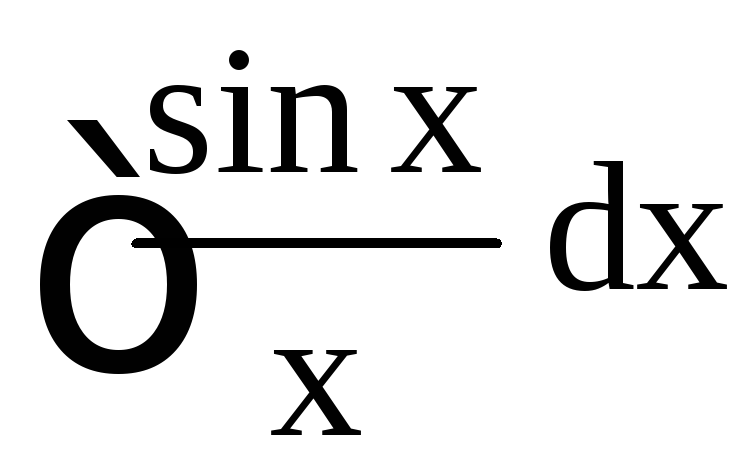,. Дело обстоит так, что в большинстве случаев решение прикладных задач требует вычисления определённых интегралов от функций, первообразные которых выходят за рамки класса элементарных функций, что делает невозможным применение формулы Ньютона–Лейбница. В таких случаях довольствуются приближённым вычислением определённого интеграла, или, как говорят, применяют методы численного интегрирования. К простейшим методам численного интегрирования относятся методы прямоугольников, трапеций и парабол (Симпсона).

Разобьём отрезок [a;b] на n равных частей точками ;называется шагом разбиения.

Обозначим  ,,.

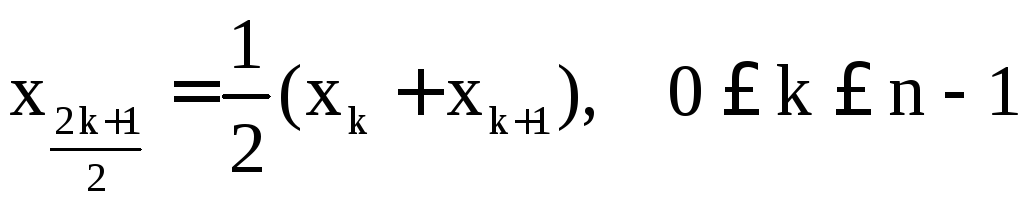По методу прямоугольников

;

;

.

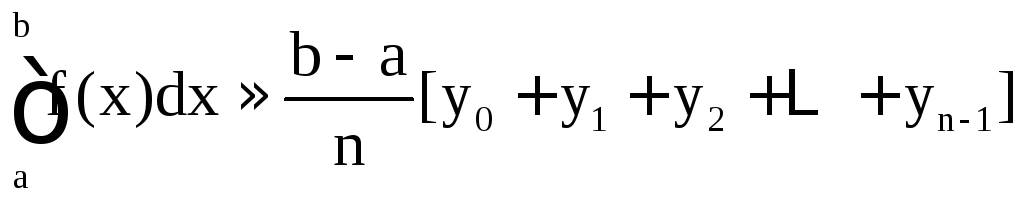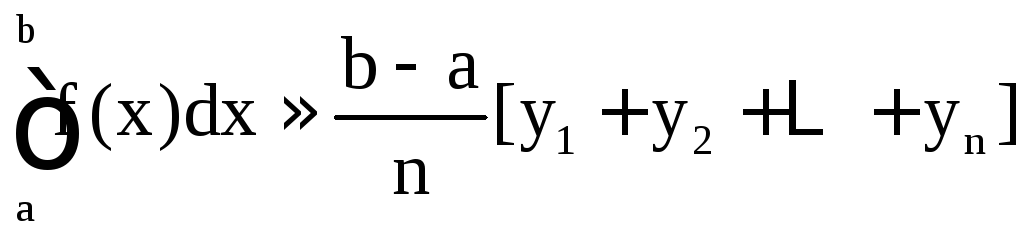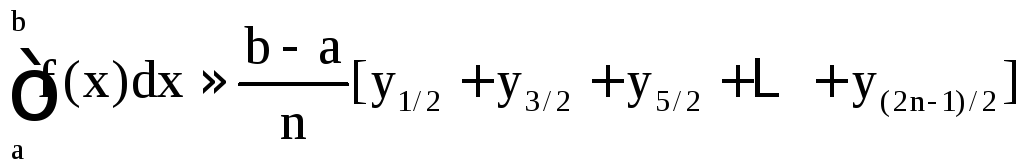Все эти три формулы называются формулами прямоугольников.

Метод трапеций состоит в применении формулы (при тех же обозначениях)

.

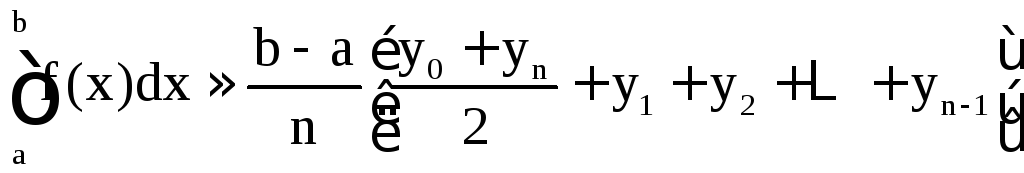В методе парабол (Симпсона) отрезок [a; b] разбивается на чётное число 2n отрезков равной длины точками a₁ = x₀ < x₁ < x₂ < …< x_2n = b. Согласно формуле Симпсона (при тех же обозначениях)

.

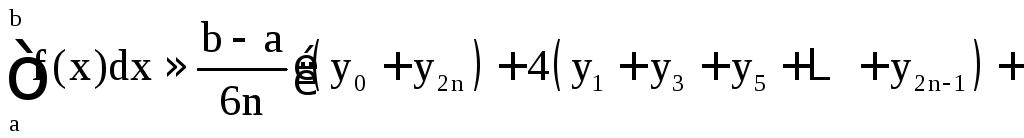
Точность вычисления растёт с ростом n. Погрешность R_n[f] приведённых выше формул оценивается величинами:

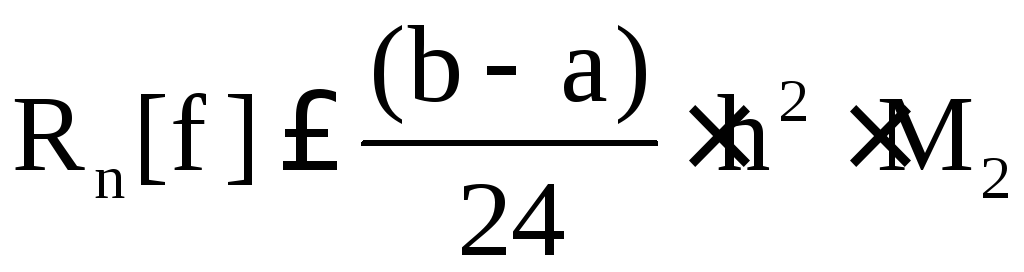для формулы прямоугольников ,

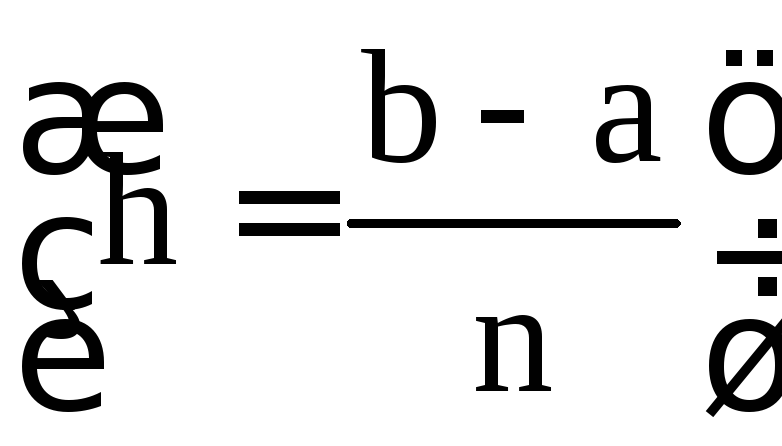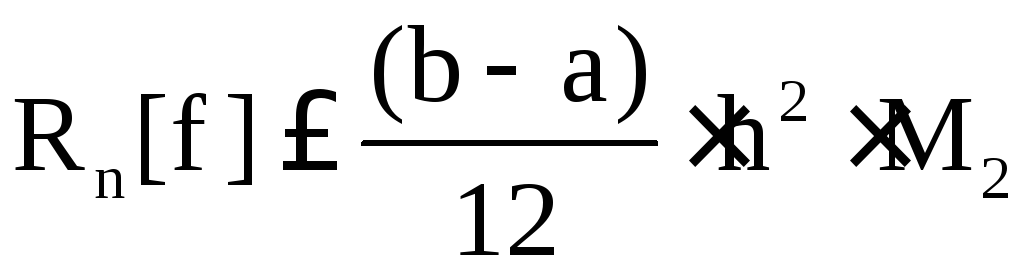для формулы трапеций ,

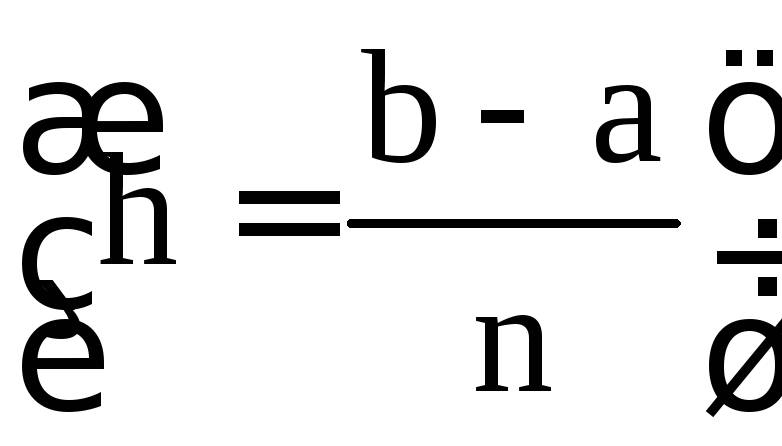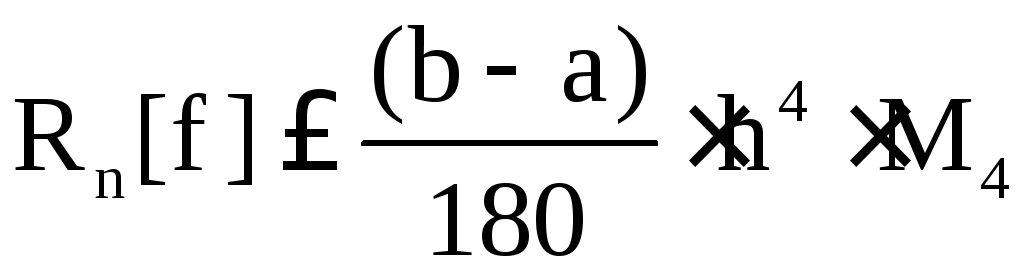для формулы Симпсона ,

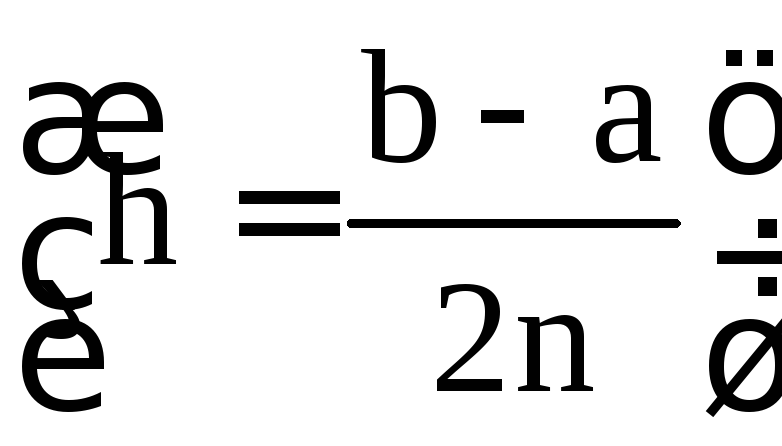где ,.

Пример 29.   Вычислите приближённо 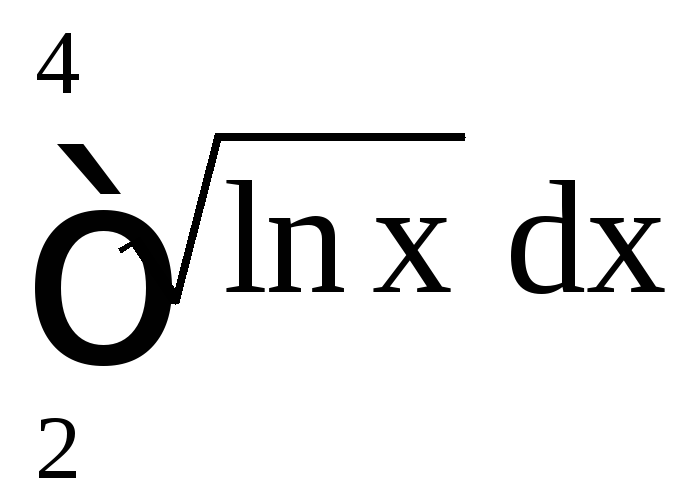методами:

а) прямоугольников, б) трапеций, в) Симпсона, взяв . В методах прямоугольников и трапеций оценить погрешность вычисления.

Решение. а) Составим таблицу .

xк	2	2,2	2,4	2,6	2,8
yк	0,8326	0,8880	0,9357	0,9775	1,0147

xк	3	3,2	3,4	3,6	3,8
yк	1,0481	1,0785	1,1062	1,1318	1,1554

Воспользуемся первой из формул прямоугольников

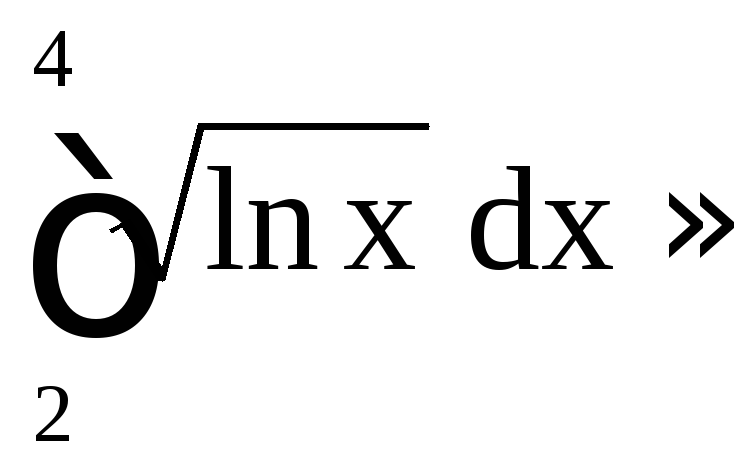0,2(0,8326 + 0,8880 + 0,9357 + 0,9775 + 1,0147 + 1,0481 + + 1,0785 + 1,1062 + 1,1318 + 1,1554) = 0,210,1685 = 2,0337.

Оценим погрешность 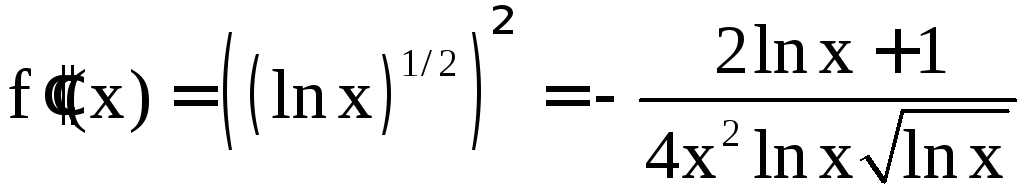. Нетрудно видеть, что.

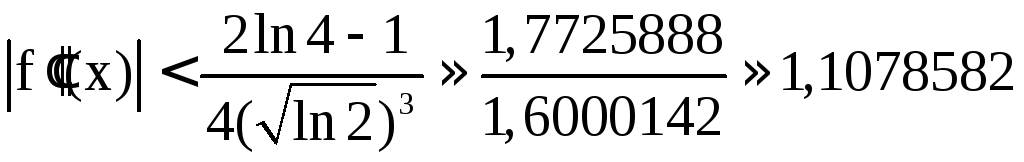Отсюда и погрешность не превышает.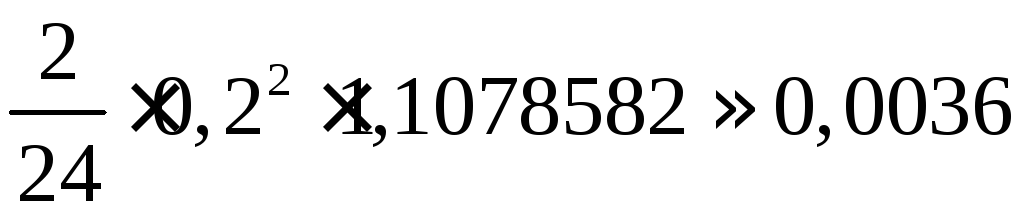

б) Для применения формулы трапеций дополним выше составленную таблицу ещё одним значением: . Имеем

.

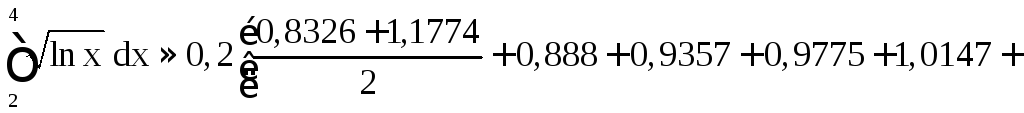
Погрешность вычисления равна .

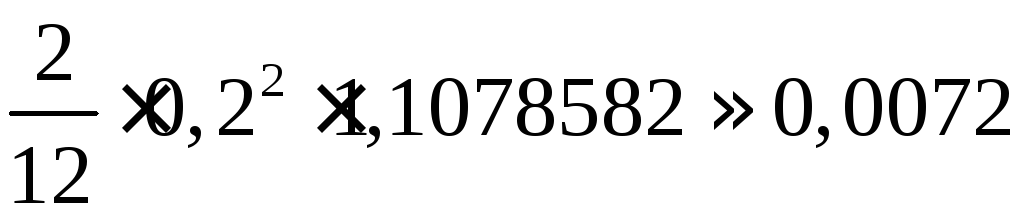в) Рассмотрим нашу таблицу (h = 0,1).

xк	2	2,1	2,2	2,3	2,4
yк	0,832555	0,861358	0,887951	0,912639	0,935665
xк	2,5	2,6	2,7	2,8	2,9
yк	0,957231	0,977503	0,996620	1,014702	1,031848
xк	3	3,1	3,2	3,3	3,4
yк	1,048147	1,063674	1,078495	1,092668	1,106244
xк	3,5	3,6	3,7	3,8	3,9
yк	1,119269	1,131784	1,143824	1,1554224	1,166609
xк	4
yк	1,177410

Отсюда находим

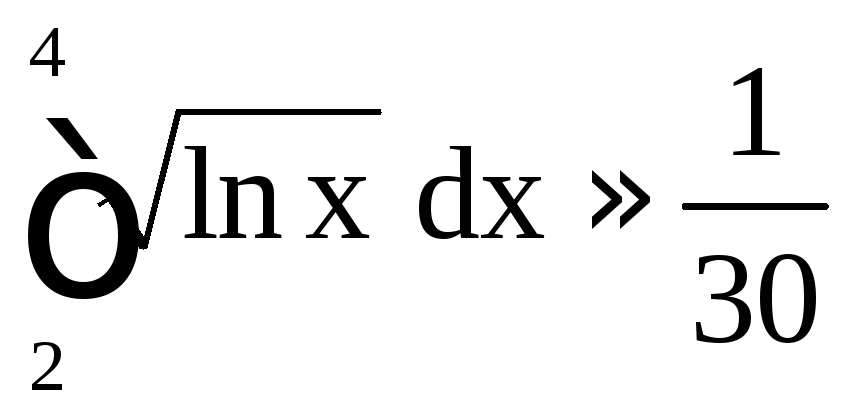[(0,832555 + 1,17741) + 4(0,861358 + 0,912639 +

+0,957231 + 0,99662 + 1,031848 + 1,063674 + 1,092668 + 1,119269 + +1,143824 + 1,166609) + 2(0,887951 + 0,935665 + 0,977503 +

+1,014702 +1,048147 +1,078495 +1,106244 + 1,131784 +1,155422)]= =62,064751 2,068825  2,0688.