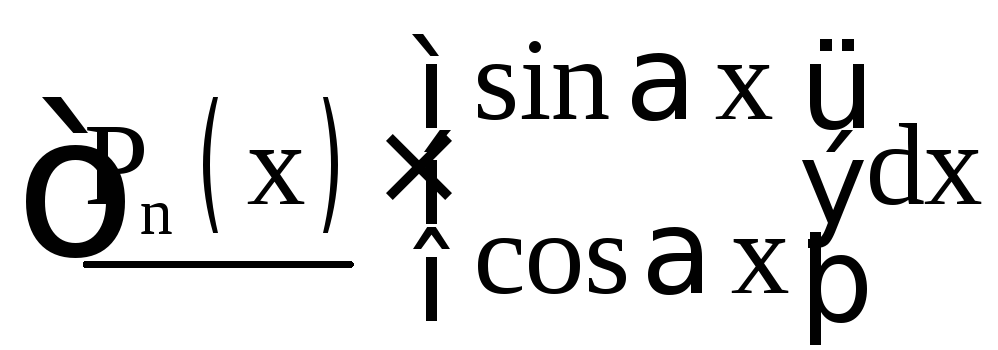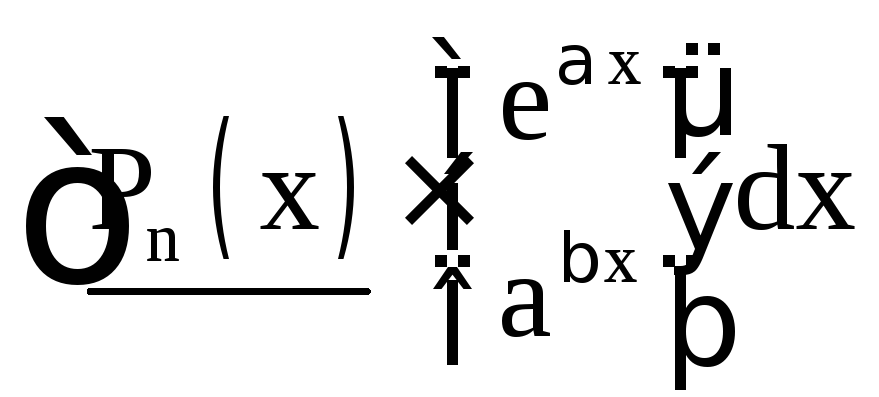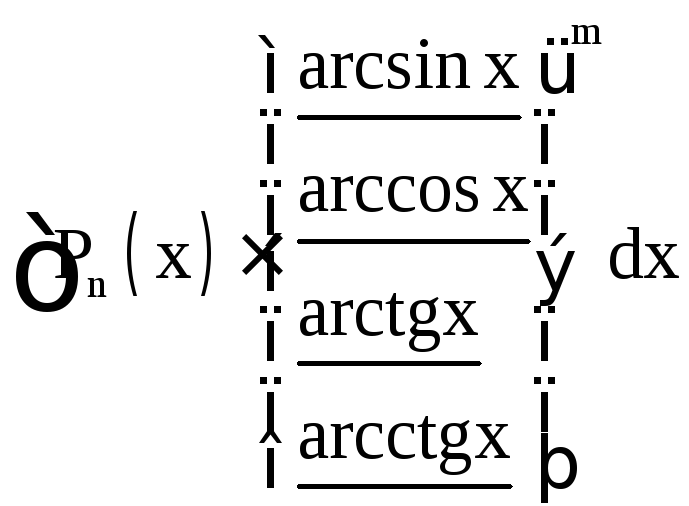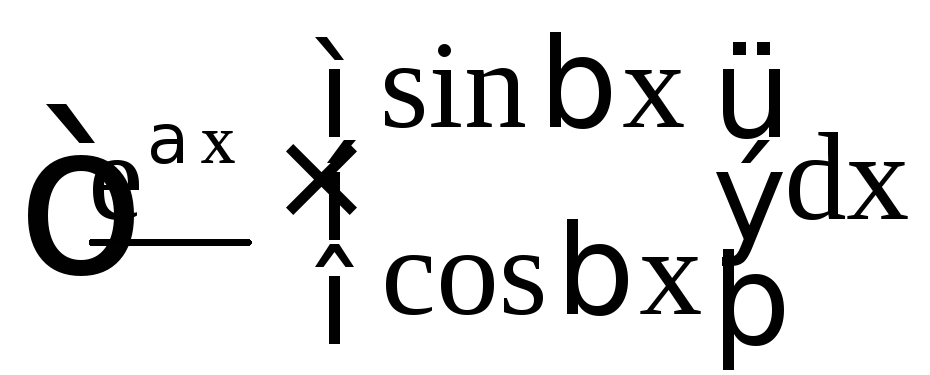- •VII. Интегральное исчисление функции одного переменного
- •1. Неопределённый интеграл
- •2. Таблица основных неопределённых интегралов
- •3. Основные свойства неопределённого интеграла
- •4. Интегрирование методом замены переменного
- •5. Интегрирование по частям
- •6. Интегрирование рациональных функций Интегрирование рациональной функции
- •7. Интегрирование тригонометрических функций
- •8. Интегрирование некоторых иррациональных функций
- •9. Определённый интеграл
- •10. Несобственные интегралы
- •11. Вычисление площадей плоских фигур
- •12. Вычисление длины дуги
- •13. Вычисление объёмов тел
- •14. Приближённое вычисление определённых интегралов
- •Задание 7.1
- •Задание 7.2
- •Задание 7.3
- •Задание 7.4
- •Задание 7.5
- •Задание 7.6
- •Задание 7.7
- •Задание 7.8
- •Задание 7.13
- •Задание 7.14
- •Задание 7.15
- •Задание 7.16
- •Задание 7.17
- •Задание 7.18
- •Задание 7.19
- •Задание 7.20
- •Задание 7.21
- •Задание 7.22
VII. Интегральное исчисление функции одного переменного
1. Неопределённый интеграл
Функция
F(x)
называется первообразной для функции
f(x),
заданной на числовом множестве X,
если
![]() для любого
для любого![]() .
Совокупность всех первообразных функцийf(x)
называется неопределённым интегралом
от f(x)
и обозначается
.
Совокупность всех первообразных функцийf(x)
называется неопределённым интегралом
от f(x)
и обозначается
![]() .
Любые две первообразные для одной
функции отличаются на константу
(постоянную величину).
.
Любые две первообразные для одной
функции отличаются на константу
(постоянную величину).
Другими
словами, имеет место равенство
![]() ,
гдеF(x)
– некоторая (фиксированная) первообразная
для f(x),
а С пробегает всевозможные числовые
значения.
,
гдеF(x)
– некоторая (фиксированная) первообразная
для f(x),
а С пробегает всевозможные числовые
значения.
Не всякая функция имеет первообразную. Однако, если f(x) – непрерывная функция, то она имеет первообразную.
2. Таблица основных неопределённых интегралов
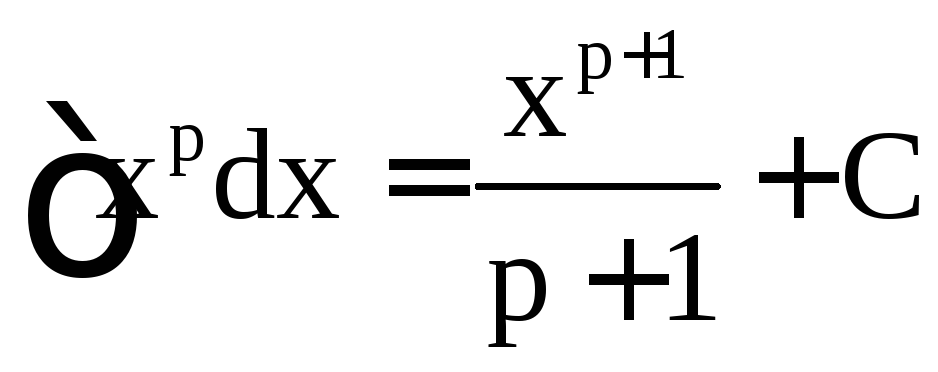 ,
,
![]()
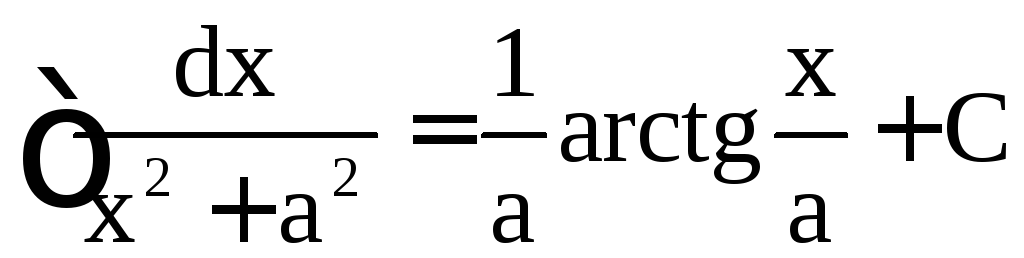
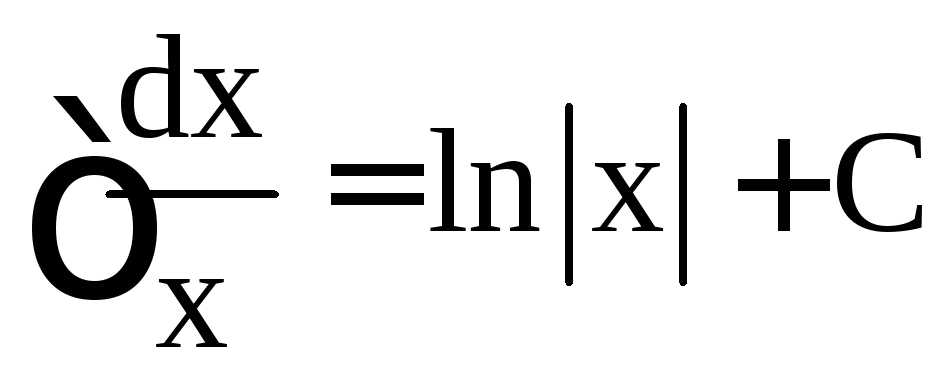 ,
, 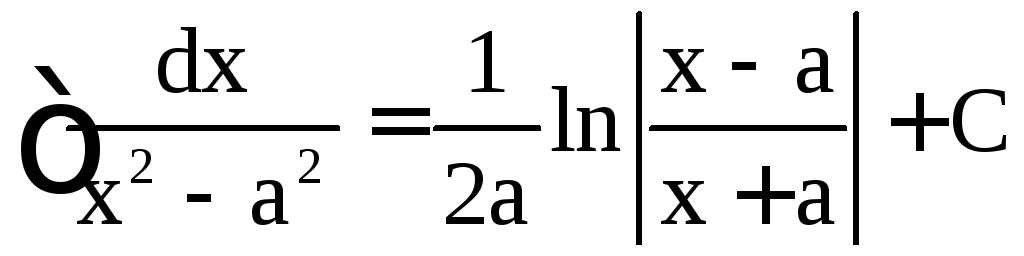 ,
,
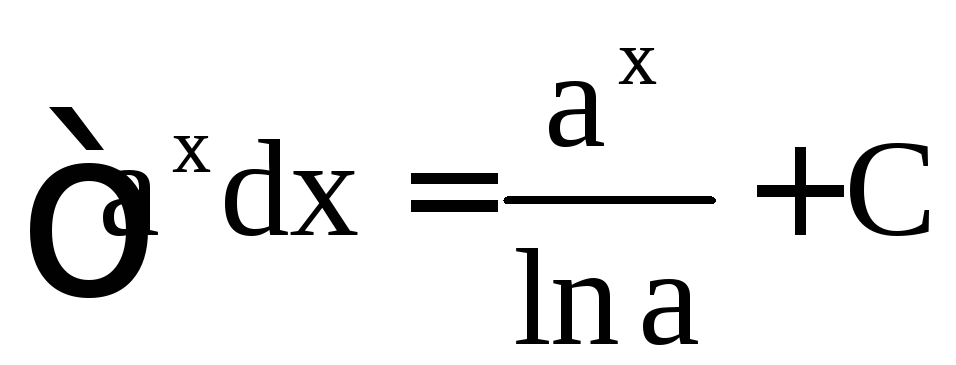 ,
, 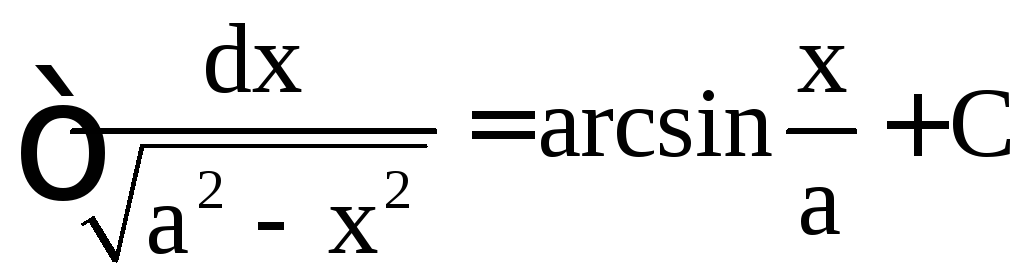 ,
,
![]() ,
, 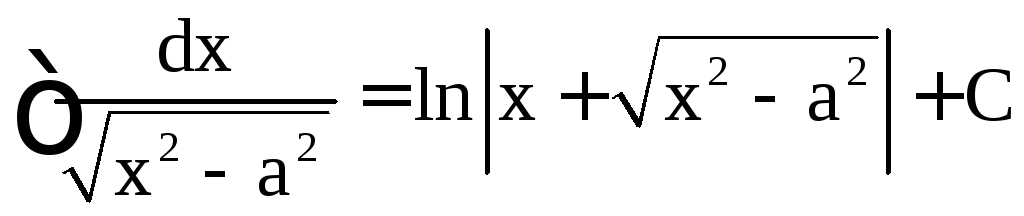 ,
,
![]() ,
, 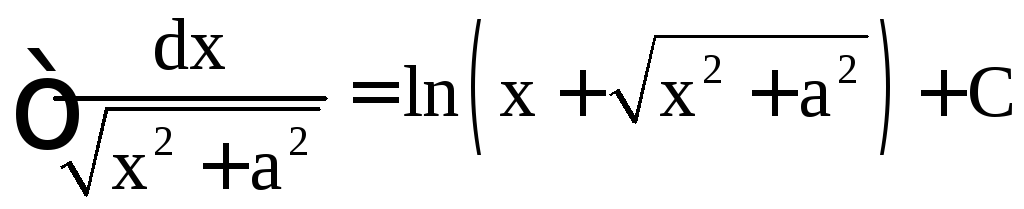 ,
,
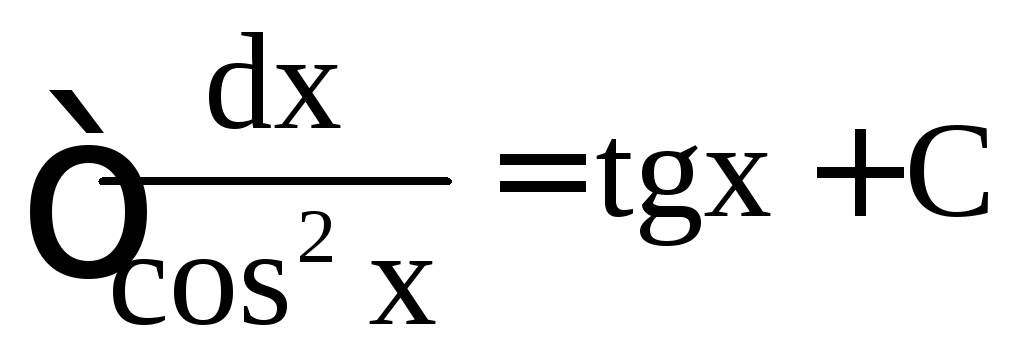 ,
, ![]() ,
,
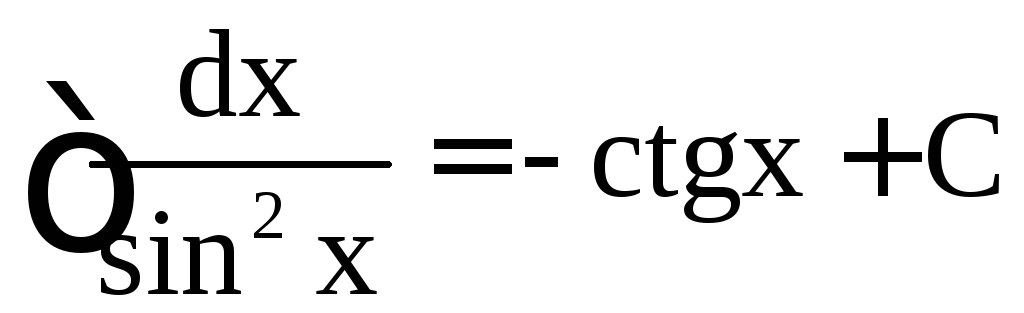 ,
, ![]() ,
,
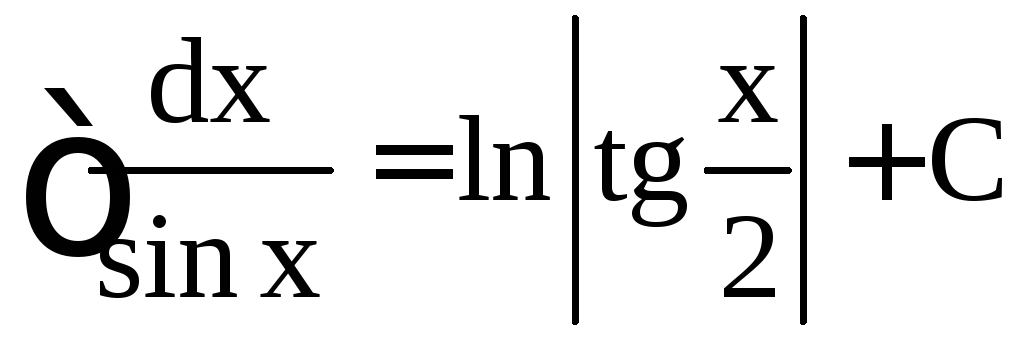 ,
, 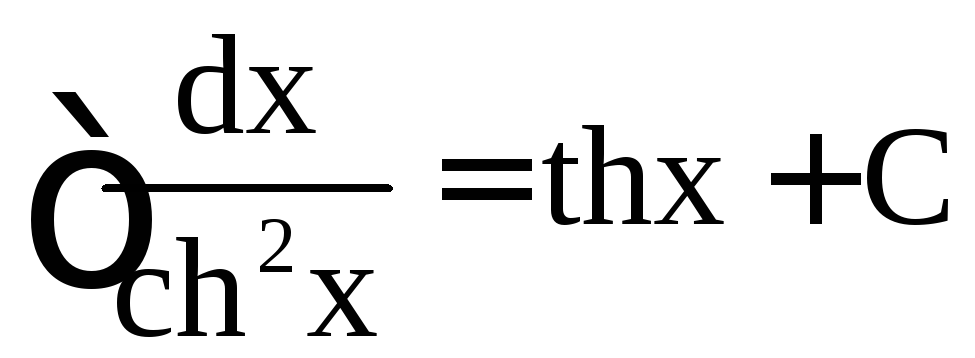 ,
,
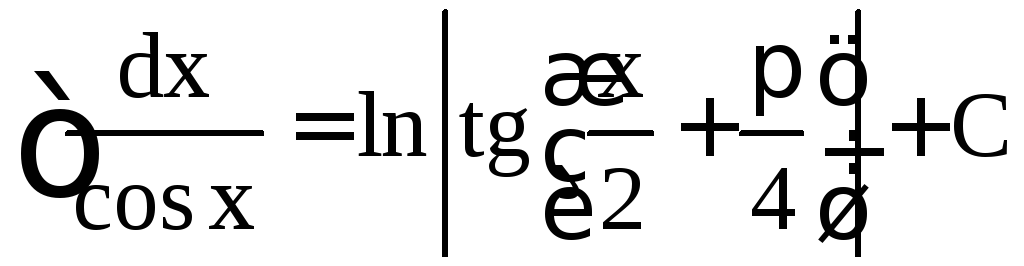 ,
, 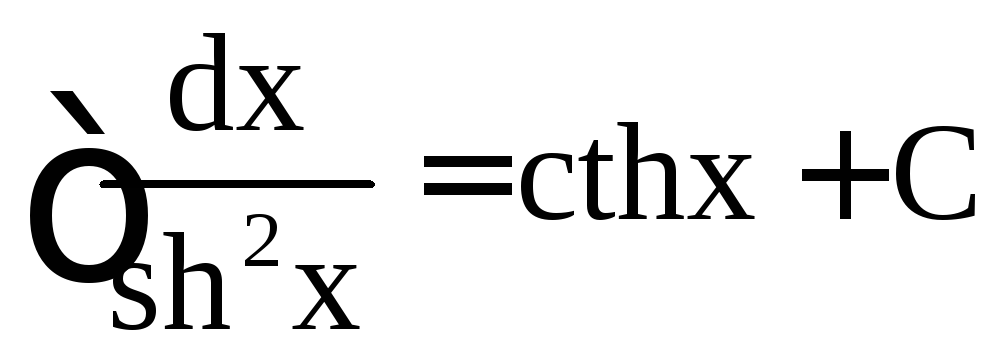 .
.
3. Основные свойства неопределённого интеграла
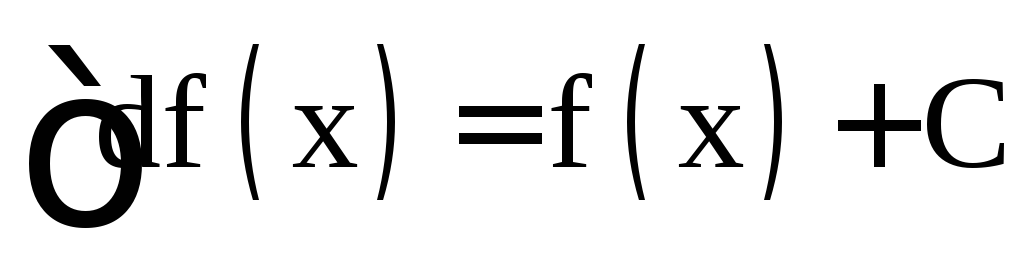 ;
;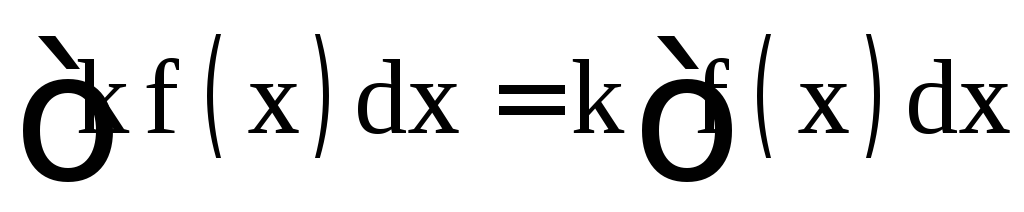 ,
где k – постоянная величина;
,
где k – постоянная величина;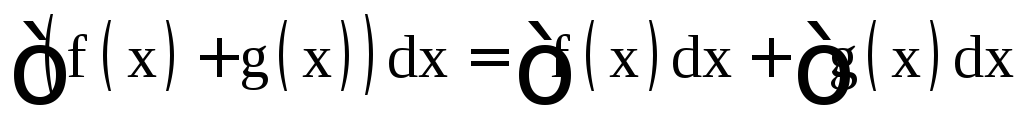 .
.
(свойства 2 и 3 составляют так называемое свойство линейности).
Пример
1. Найти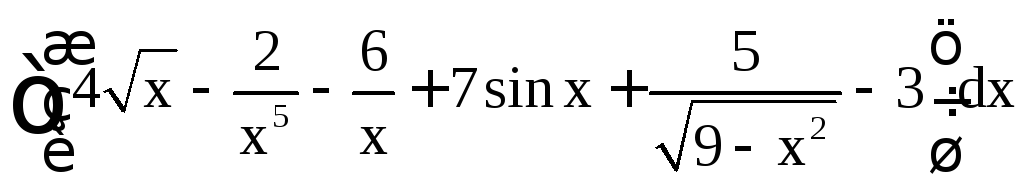 .
.
Решение.
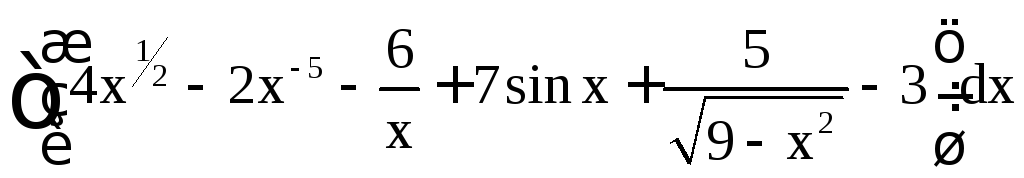 =
=
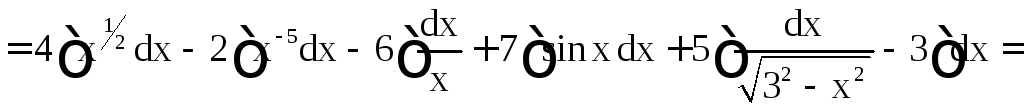
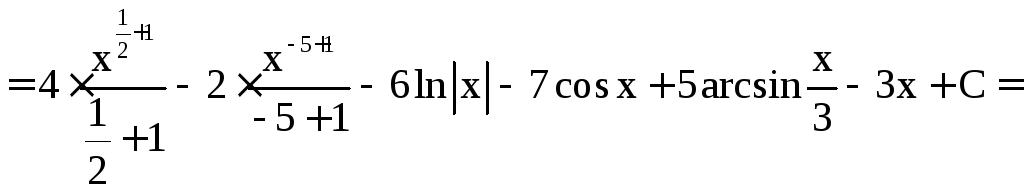
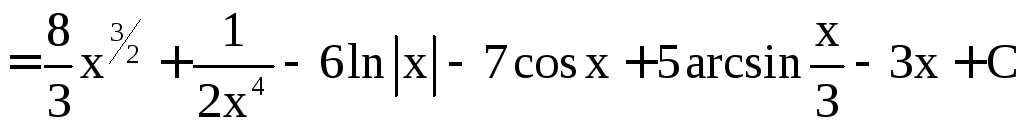 .
.
4. Интегрирование методом замены переменного
Теорема 1.
Если
![]() и
и
![]() ,
то при условии дифференцируемости
функции (x)
справедлива формула
,
то при условии дифференцируемости
функции (x)
справедлива формула
![]() или
или
![]() .
.
Теорема 1 значительно расширяет таблицу простейших интегралов. А именно, в силу этой теоремы таблица интегралов оказывается справедливой независимо от того, является переменная интегрирования независимой переменной или дифференцируемой функцией.
Напомним формулу
для дифференциала функции
![]() ,
,![]() (*),
которая часто используется при вычислении
интегралов.
(*),
которая часто используется при вычислении
интегралов.
Пример 2.
Найти интегралы: а)
![]() ;
б)
;
б)![]() ;
в)
;
в)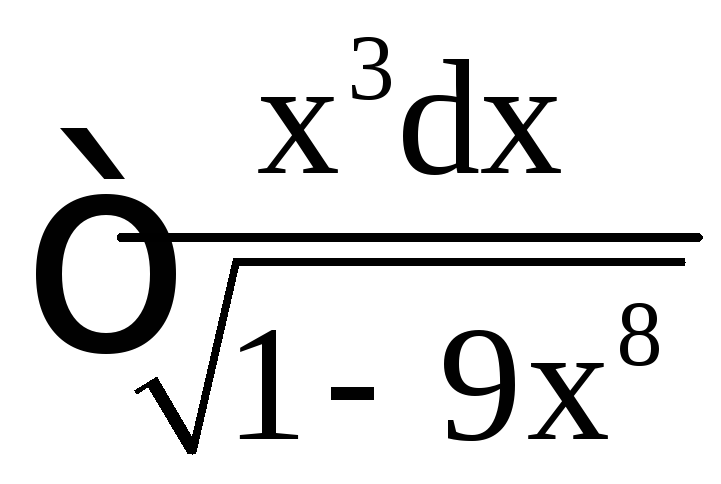 .
.
Решение.
а)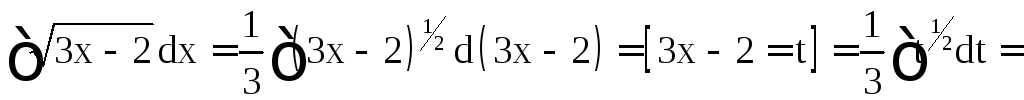
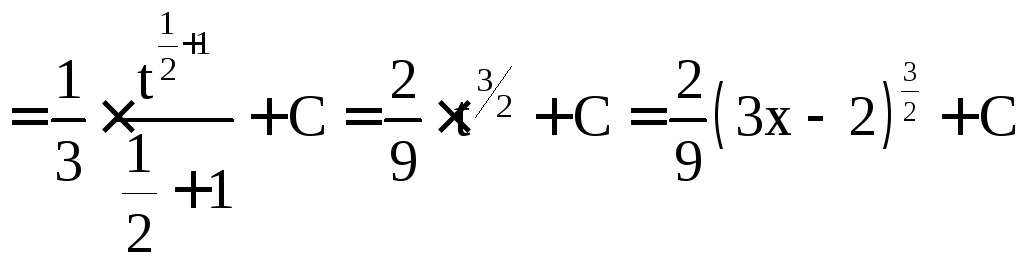 ;
;
б)
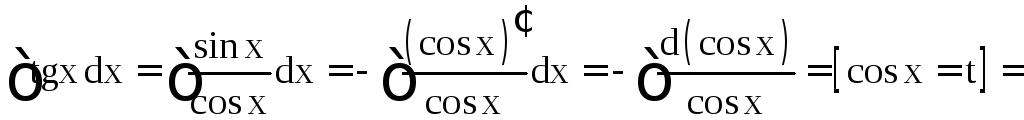
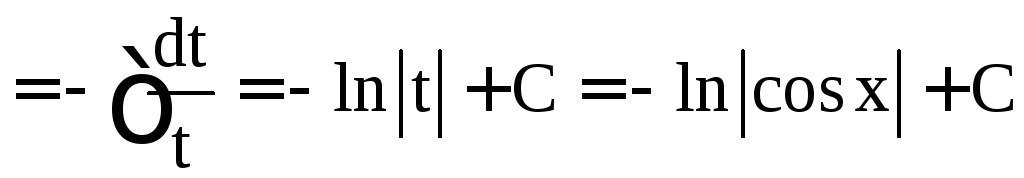 ;
;
в)
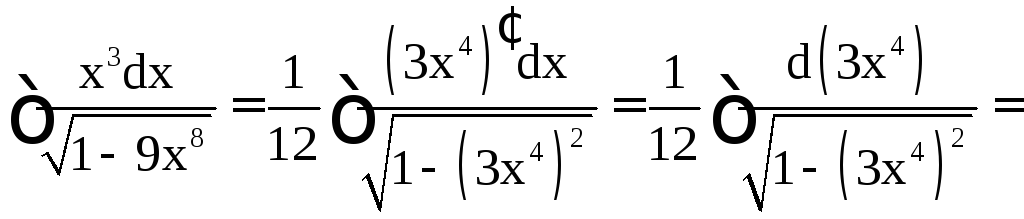
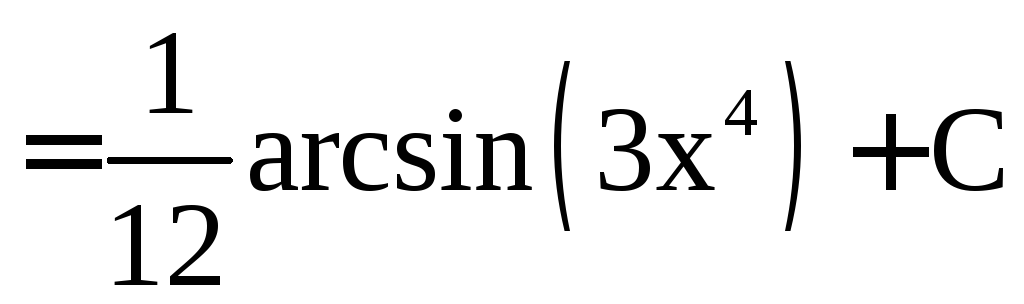 .
.
Пример
3. Найти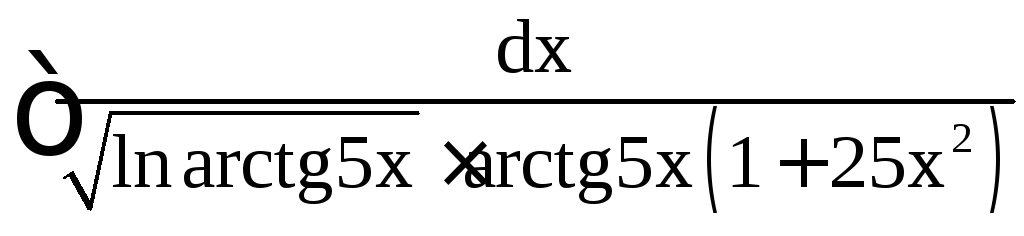 .
.
Решение.
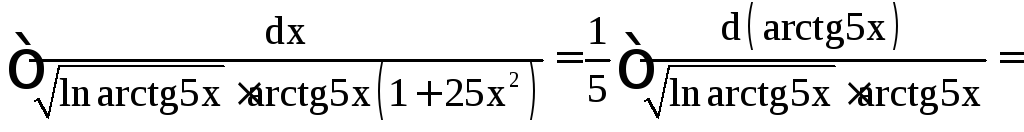
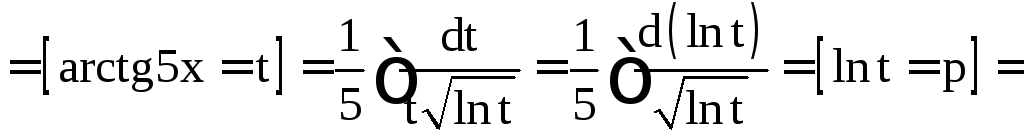
![]()
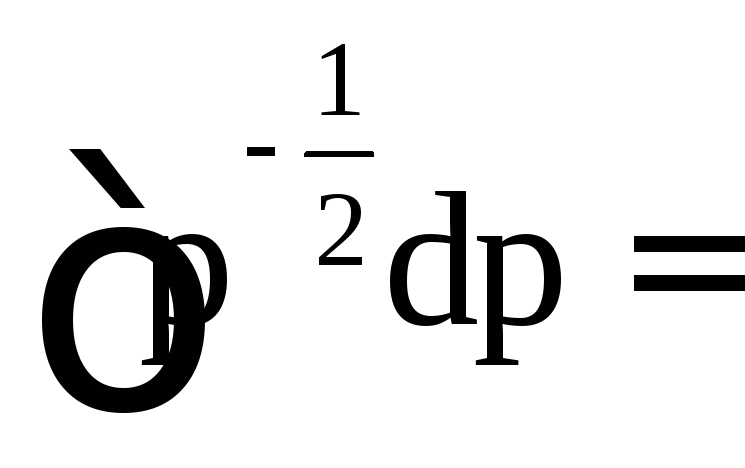
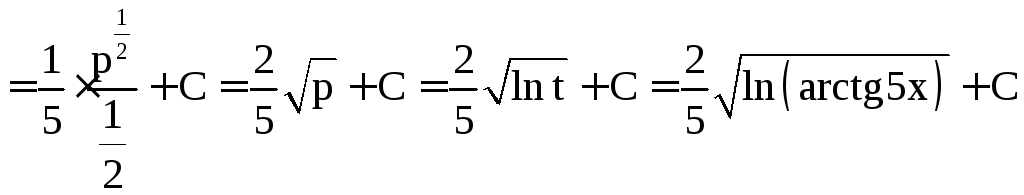 .
.
Этот пример можно решить ещё и так:
![]() ,
,
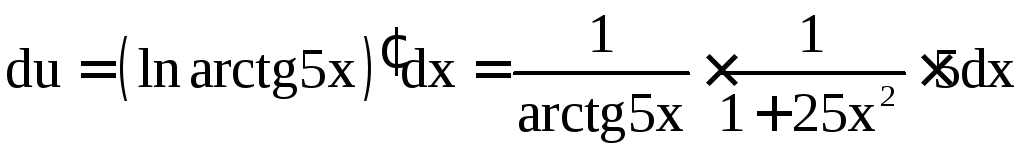 ;
;
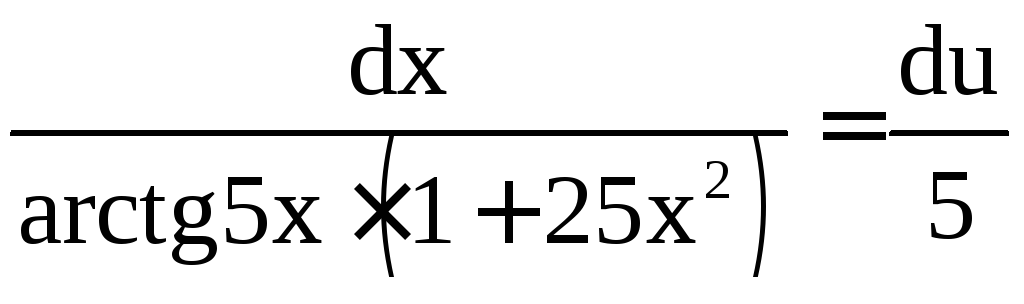 ;
;
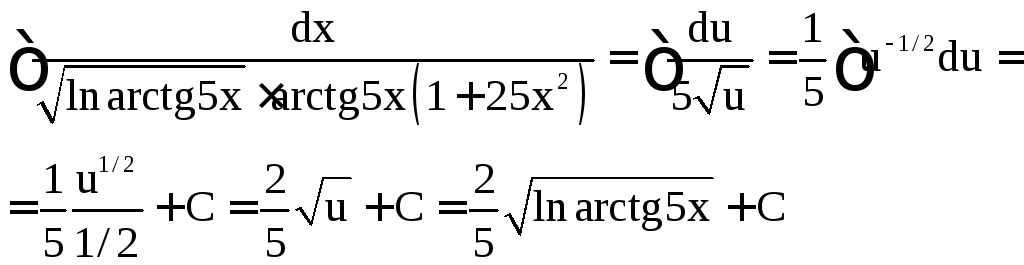
Пример
4.Найти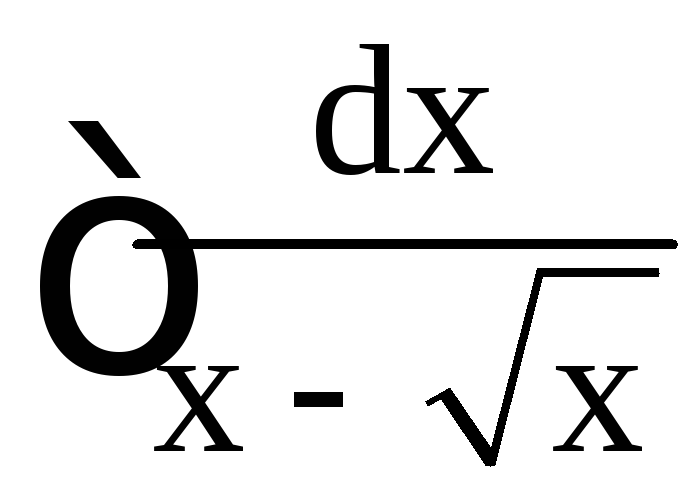 .
.
Решение.Положим![]() .
.
Тогда
![]() и
и
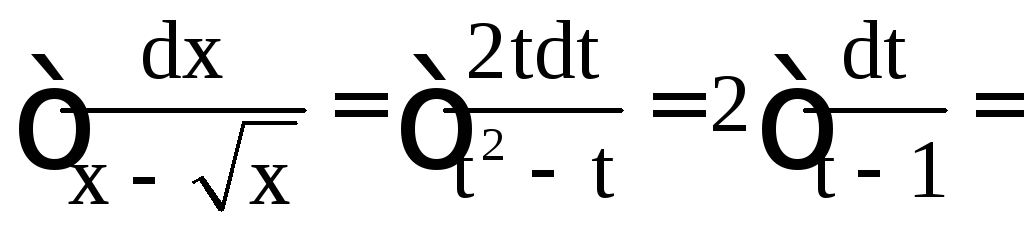
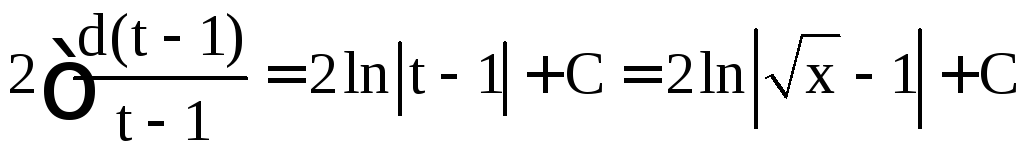 .
.
Пример
5. Найти
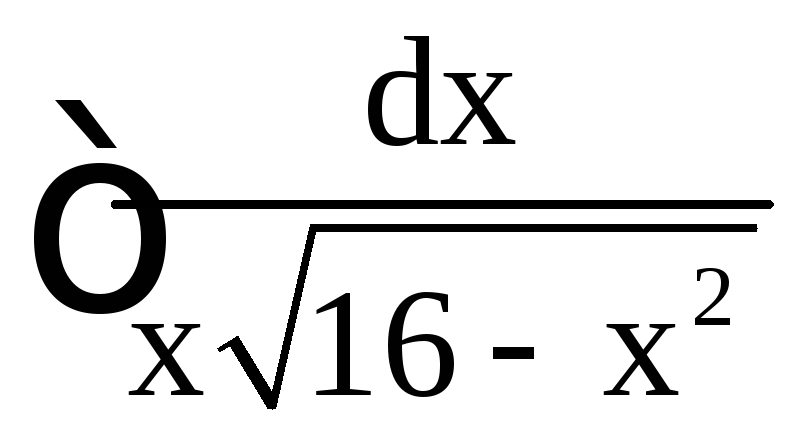 .
.
Решение.
Применим подстановку
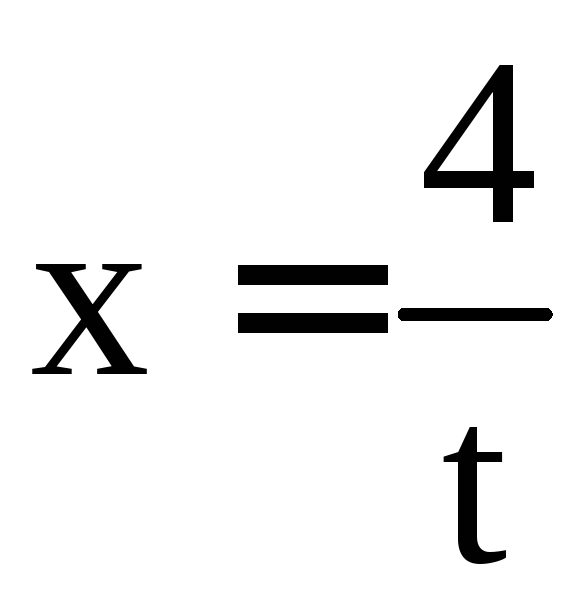 .
.
Тогда
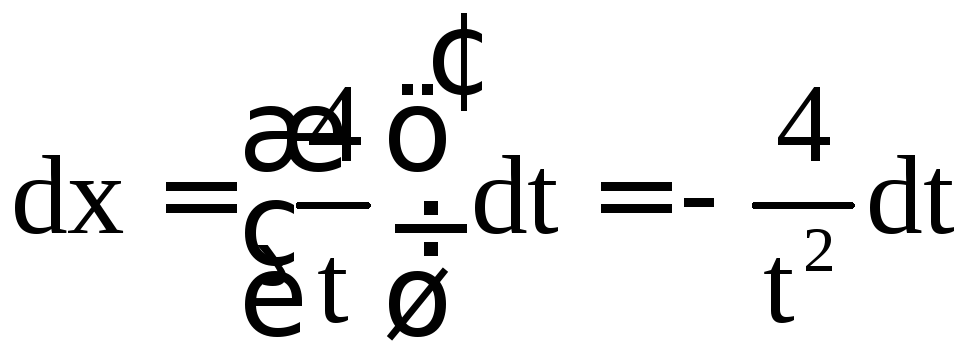 .
.
Имеем
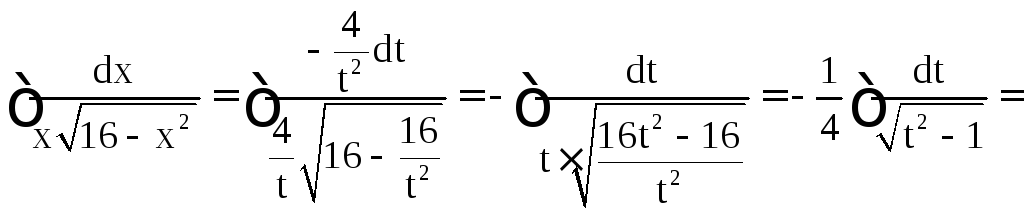
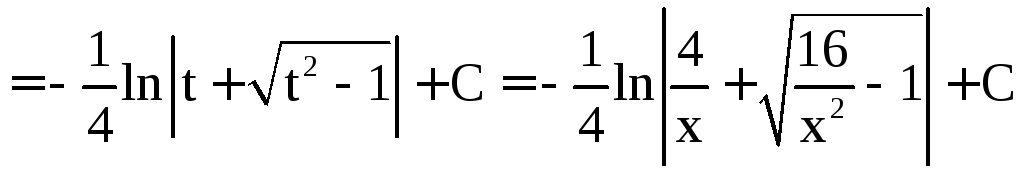 .
.
5. Интегрирование по частям
Если u(x), v(x) дифференцируемы, то справедлива формула интегрирования по частям
![]() .
.
Эту формулу следует применять в тех случаях, когда подынтегральное выражение vdu проще исходного выражения udv.
Ниже приведены основные типы интегралов, берущихся по частям.
|
I тип |
II тип |
III тип (интегралы, приводящиеся к себе) |
|
|
|
|
За u принимаются
подчёркнутые функции, за dv – остальная
часть подынтегрального выражения. Pn
(x) – многочлен степени n. Интегралы I
типа берутся путём интегрирования по
частям n раз, II типа – m раз, III типа (за
исключением двух последних) – 2 раза
(причём, в первом интеграле III типа оба
раза за u можно принять как
![]() ,
так и тригонометрические функции
,
так и тригонометрические функции![]() ,
,![]() ).
).
По частям могут быть взяты и интегралы, не вошедшие в эту таблицу.
Пример 6. Найти интегралы:
а)![]() ; б)
; б)![]() ; в)
; в)![]() .
.
Решение.
а)
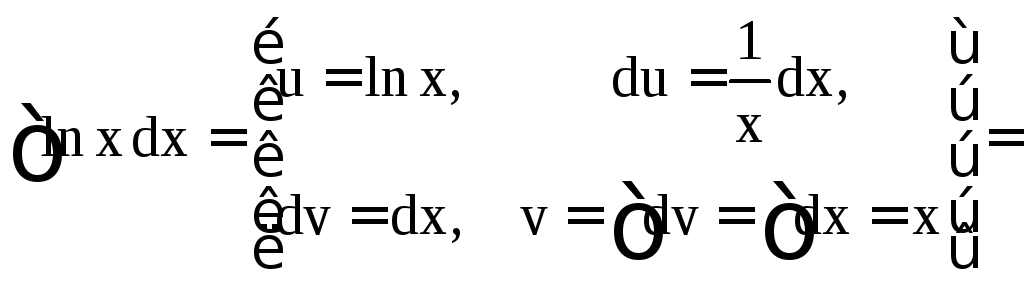
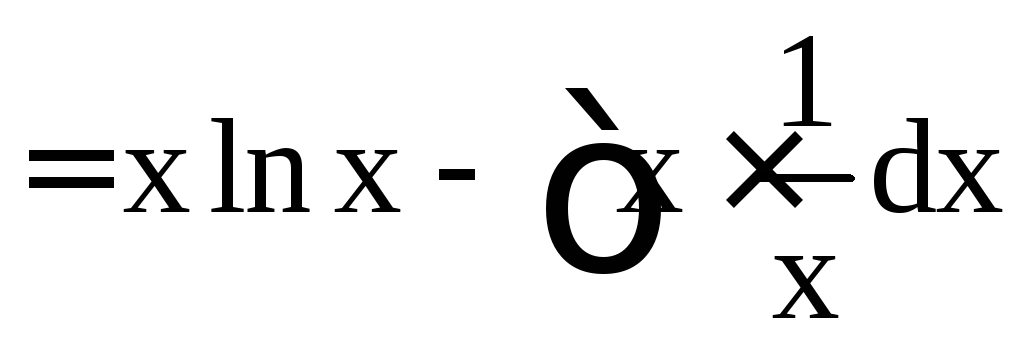
![]() .
.
Здесь и ниже при нахождении v при известном dv мы полагаем С = 0 (как в этом случае: dv = dx, отсюда следует v = x + C, но мы берём одну из первообразных v = x).
б)
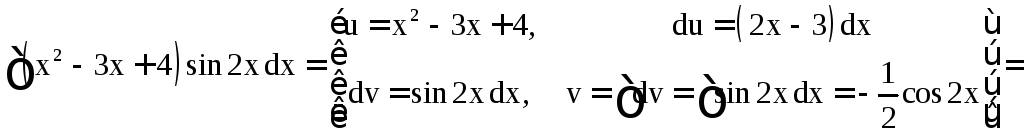
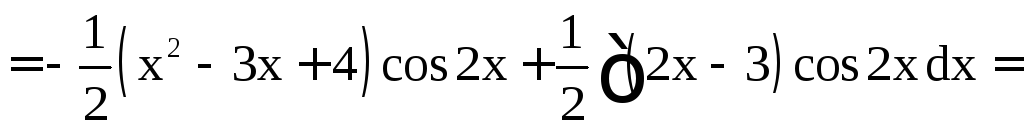
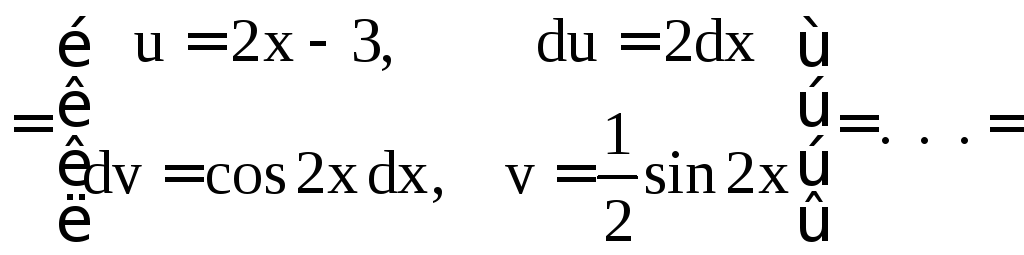
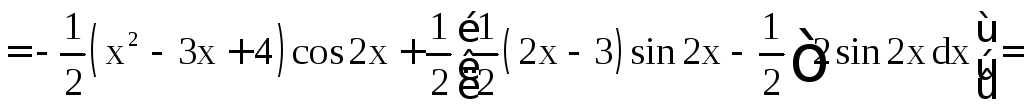
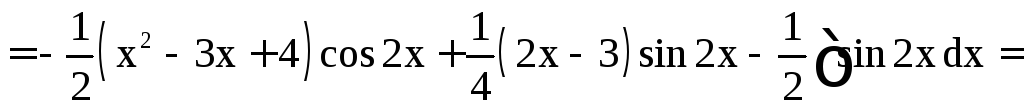
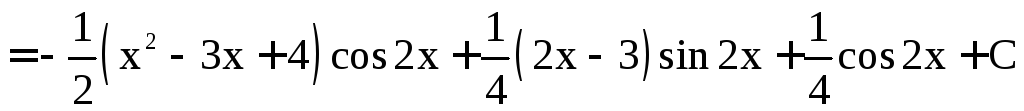 .
.
в) Обозначим
![]() .
Имеем
.
Имеем
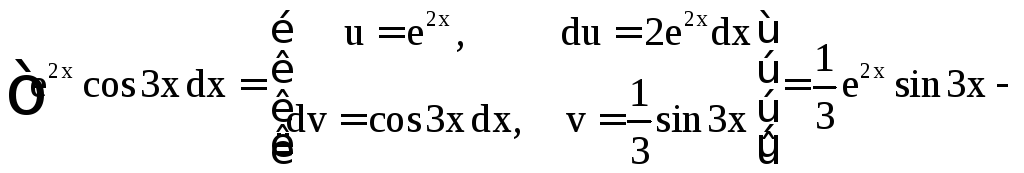
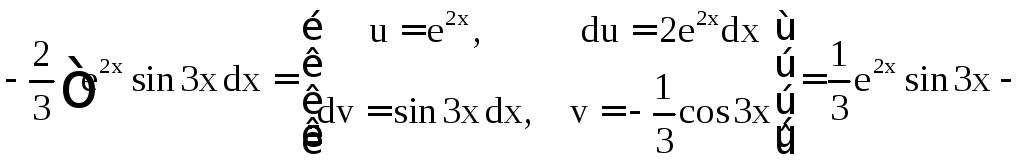
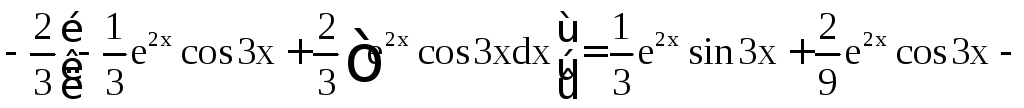
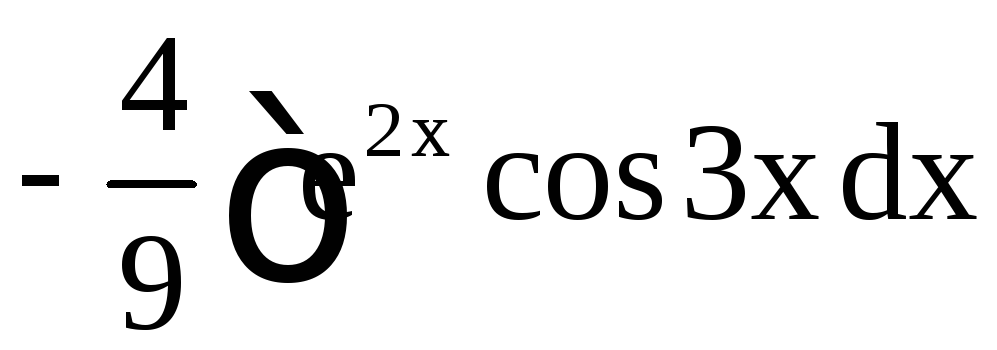 .
.
Получается, что
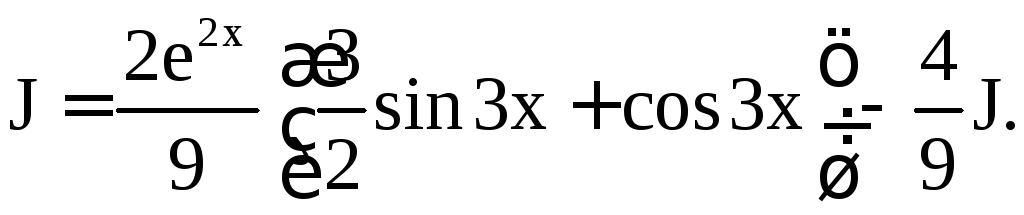
Отсюда находим (учитывая, что J является семейством функций, отличающихся друг от друга на постоянную величину)
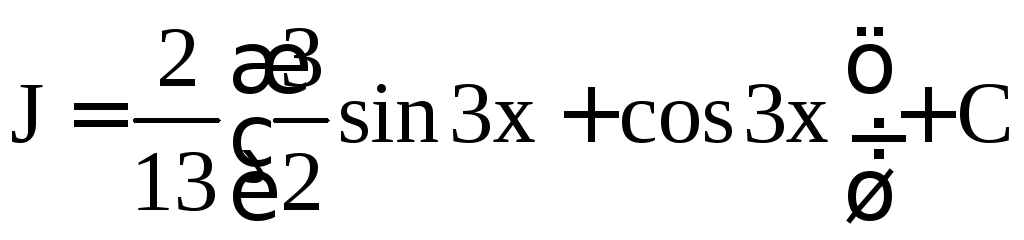 .
.